Long Division – The Bus Stop Method

GCSEKS3Level 1-3AQAEdexcelOCRWJEC

Long Division – The Bus Stop Method Revision

Long Division

There are different methods that can be used for long division but the most commonly used in the UK is the Bus Stop method.

Bus Stop Method

This method for long division is called the Bus Stop method, since it looks like a bus stop. This method allows us to divide numbers to find integer answers or answers that have a remainder. There are a few steps that you need to follow.

Example: Calculate $288 \div 9$ .

Step 1: We start by putting the division into the Bus Stop form as show below.

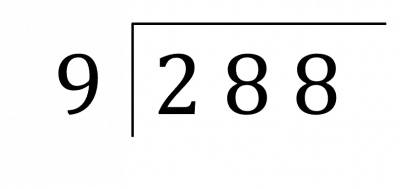
Step 2: We see how many times $9$ goes into $2$ , the first digit. The answer is $\textcolor{blue}{0}$ so the $\textcolor{red}{2}$ is carried onto the next digit to make a new number, $28$ . The zero goes at the top.

Step 3: Now, we see how many times $9$ goes into $28$ . We know that $3 \times 9=27$ , so $9$ goes into $28$ $\textcolor{blue}{3}$ times with a remainder $\textcolor{red}{1}$ , which is then carried in front of the next digit to make a new number, $18$ . The three goes at the top.

Step 4: Then, we see how many times the $9$ goes into $18$ , which is $\textcolor{blue}{2}$ . The two then goes at the top. These two steps are combined in the image below.

So,

$288 \div 9 = \textcolor{limegreen}{32}$

Note: If $9$ did not go into the number in the last step, for example if the question asked to calculate $289 \div 9$ , then $9$ goes into $19$ $\textcolor{blue}{2}$ times, with a remainder $\textcolor{red}{1}$ . So we would say that the answer had a remainder of $1$ and we would write

$289 \div 9 = \textcolor{limegreen}{32} \text{ r } \textcolor{red}{1}$

Example: Long Division with a Remainder

Calculate $67 \div 5$

[2 marks]

We use the same bus stop method as shown before, but this time we have a remainder.

$67 \div 5 = \textcolor{limegreen}{13} \text{ r } \textcolor{red}{2}$

Long Division – The Bus Stop Method Example Questions

Question 1: Work out $315 \div 14$ .

[2 marks]

Here we’re going to use the bus stop method.

$14$ goes into $3$ zero times, so we write a zero above the line and a small $3$ – the remainder – in between the $3$ and the $1$ . Then, we see how many times $14$ goes into $31$ , writing the result above the line and the remainder just before the next digit of the dividend.

Repeat this process until you get the complete answer, which looks like,

$\;\;\;\;\;0\;2\;2\;.\;5\\14\overline{\left)3{}^31{}^35.{}^70\right.}$

Save your answers with

Gold Standard Education

Question 2: Calculate $225 \div 15$ .

[2 marks]

Here we’re going to use the bus stop method,

$15$ goes into $2$ zero times, so we write a zero above the line and a small $2$ – the remainder – in between the $2$ and the $2$ . Then, we see how many times $15$ goes into $22$ , which is $1$ , writing the result above the line and the remainder, $7$ , just before the next digit of the dividend.

Repeat this process until you get the complete answer, which looks like,

$\;\;\;\;\;0\;1\;5\\15\overline{\left)2{}^22{}^75\right.}$

Save your answers with

Gold Standard Education

Question 3: Calculate $4320 \div 160$ .

[2 marks]

Here we’re going to use the bus stop method,

$160$ goes into $4$ zero times, so we write a zero above the line and a small $4$ – the remainder – in between the $4$ and the $3$ . Then, we see how many times $160$ goes into $43$ , which is also zero, writing the result above the line and the remainder, $43$ , just before the next digit of the dividend.

Repeat this process until you get the complete answer, which looks like,

$\;\;\;\;\;\;\;0\;\;0\;\;2\;\;7\\160\overline{\left)4{}^43{}^{43}2{}^{112}0\right.}$

Save your answers with

Gold Standard Education

Question 4: Calculate $299 \div 13$ .

[2 marks]

Here we’re going to use the bus stop method,

$13$ goes into $2$ zero times, so we write a zero above the line and a small $2$ – the remainder – in between the $2$ and the $9$ . Then, we see how many times $13$ goes into $29$ , which is $2$ , writing the result above the line and the remainder, $3$ , just before the next digit of the dividend.

Repeat this process until you get the complete answer, which looks like,

$\;\;\;\;0\;2\;3\\13\overline{\left)2{}^29{}^39\right.}$

Save your answers with

Gold Standard Education

Question 5: Calculate $234 \div 9$ .

[2 marks]

Here we’re going to use the bus stop method,

$9$ goes into $2$ zero times, so we write a zero above the line and a small $2$ – the remainder – in between the $2$ and the $3$ . Then, we see how many times $9$ goes into $23$ , which is $2$ , writing the result above the line and the remainder, $5$ , just before the next digit of the dividend, so we find,

$\;\;\;0\;2\;6\\9\overline{\left)2{}^23{}^54\right.}\\\;\;\;\;\;\;\;\;$

Save your answers with

Gold Standard Education