Revise
Long Multiplication
Long Multiplication Revision
Long Multiplication and Grid Method
The 2 multiplication methods we will see are the long multiplication (column) method and the grid method. The grid method is taught by many schools in the UK but there are many that prefer long multiplication, so we will look at both.
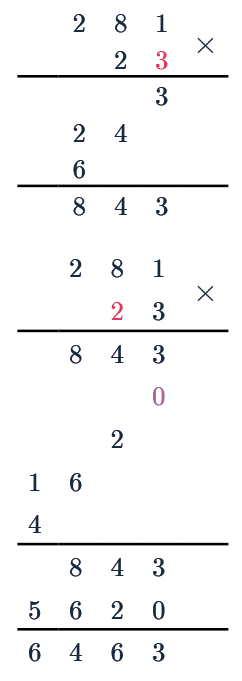
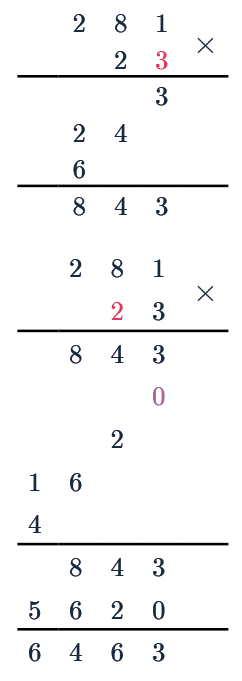
Method 1: Long Multiplication (Column) Method
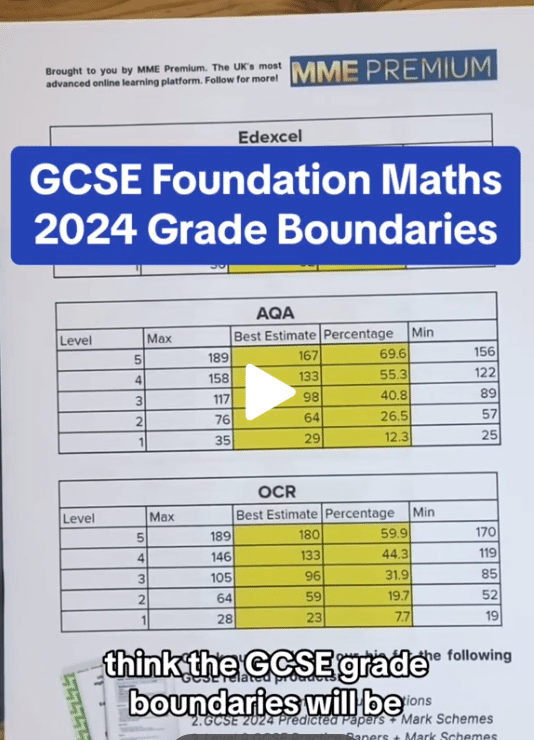
Step 1: Write the two numbers we are multiplying on top of each other, usually with the bigger one on top. We write the values so that the 1s, 10s, 100s and so on all line up in the correct column.
Step 2: Multiply the last digit from the bottom number with every digit from the top number, writing the results underneath from right to left, and carrying forward when values go above 10.
3\times1 = 3, 3\times8=24, 3\times2 = 6
Step 3: Next, the second digit is the tens digit, for this we write a 0 underneath the last step’s working so that everything is shifted one space to the left.
We then multiply this digit by every digit from the top number, writing the results underneath the last step from right to left.
Step 4: Add up the final numbers using the column addition method, writing the results under another line.
From this we can see:
281 \times 23 = 6463
Method 2: The Grid Method
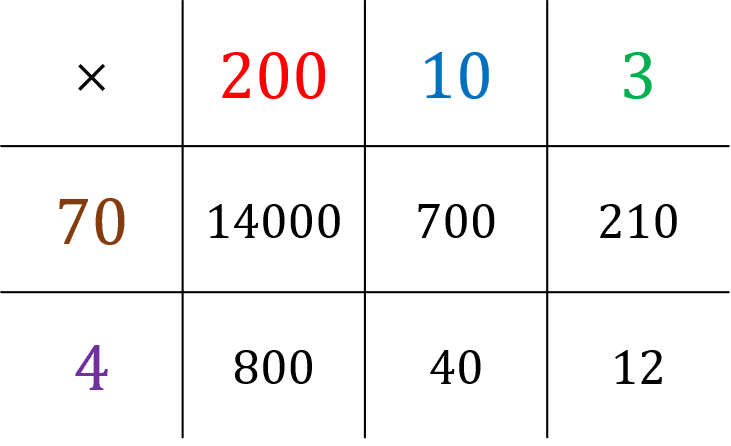
Step 1: Split each number into 1s, 10s, 100s and so on, and write each component of one number along the top of a grid, and each component of the other number down the left-hand side.
\textcolor{red}{2}\textcolor{blue}{1}\textcolor{limegreen}{3} \times \textcolor{maroon}{7}\textcolor{purple}{4}
Step 2: Fill all the squares of the grid by multiplying each part of one number by each part of the other.
Step 3: We add up all the answers from the grid to get our final answer.
14000+800+700+210+40+12=15762
Example: The Grid Method
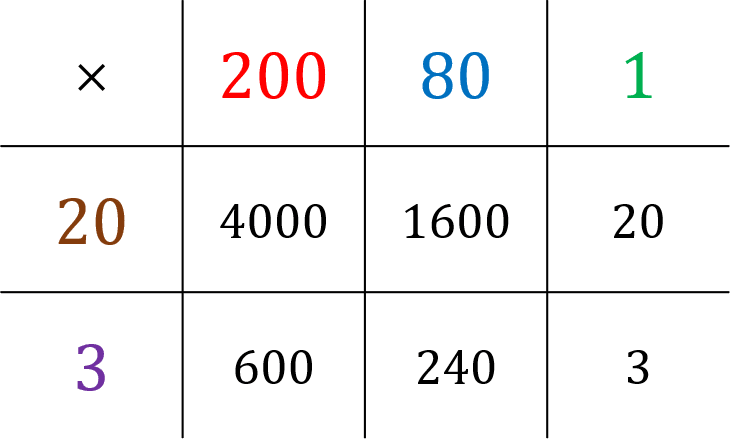
Work out 23\times 281, without using a calculator.
[3 marks]
Split each number into 1s, 10s, 100s and so on, writing each component of one number along the top of the grid, and each component of the other number down the left-hand side. Then, fill all the squares of the grid by multiplying each bit of one number by each bit of the other number.
Then, by whichever method you prefer, add together all the answers in the grid.
4000+1600+600+240+20+3=6463
So,
281 \times 23 = 6463
Long Multiplication Example Questions
Question 1: Work out 45 \times 619, without using a calculator.
[3 marks]
For this multiplication we will use the long multiplication method, multiplying 619 first by 5 then by 40,
\begin{array}{r}619\\\times45\\\hline3095\\24760\end{array}
Adding the results of each components multiplication,
\begin{array}{r}\begin{array}{r}3095\\+24760\\\hline27855\end{array}\end{array}
Question 2: Calculate 52 \times 31, without using a calculator.
[3 marks]
For this multiplication we will use the long multiplication method, multiplying 52 first by 1 then by 30,
\begin{array}{r}\begin{array}{r}52\\\times31\\\hline52\\1560\end{array}\end{array}
Adding the results of each components multiplication,
\begin{array}{r}\begin{array}{r}52\\+1560\\\hline1612\end{array}\end{array}
Question 3: Calculate 24 \times 760, without using a calculator.
[3 marks]
For this multiplication we will use the long multiplication method, multiplying 760 first by 4 then by 20,
\begin{array}{r}\begin{array}{r}760\\\times24\\\hline3040\\15200\end{array}\end{array}
Adding the results of each components multiplication,
\begin{array}{r}\begin{array}{r}3040\\+15200\\\hline18240\end{array}\end{array}
Question 4: Calculate 52 \times 364, without using a calculator.
[3 marks]
For this multiplication we will use the long multiplication method, multiplying 364 first by 2 then by 50,
\begin{array}{r}\begin{array}{r}364\\\times52\\\hline728\\18200\end{array}\end{array}
Adding the results of each components multiplication,
\begin{array}{r}\begin{array}{r}728\\+18200\\\hline18928\end{array}\end{array}
Question 5: Calculate 38 \times 185, without using a calculator.
[3 marks]
For this multiplication we will use the long multiplication method, multiplying 185 first by 8 then by 30,
\begin{array}{r}\begin{array}{r}185\\\times38\\\hline1480\\5550\end{array}\end{array}
Adding the results of each components multiplication,
\begin{array}{r}\begin{array}{r}1480\\+5550\\\hline7030\end{array}\end{array}
Long Multiplication Worksheet and Example Questions
(NEW) Long Multiplication - Exam Style Questions - MME
Level 1-3GCSEKS3NewOfficial MME
