Revise
Time
Time Revision
Time
Time is a very important measurement.
Time can be recorded in many different ways:
- 12 hour clocks
- 24 hour clocks
- Analogue clocks
- Digital clocks
- Timetables
Units of Time
Time has various different units, the majority of which you should already be familiar with.
In your exam, you may need to convert between different units of time.
Shown below are some common conversions you need to know:
| 60 seconds | =1 minute |
| 60 minutes | =1 hour |
| 24 hours | =1 day |
| 7 days | =1 week |
| 365 days | =1 year |
| 52 weeks | =1 year |
| 12 months | =1 year |
| 10 years | =1 decade |
| 100 years | =1 century |
We can also divide 1 hour into fractions of an hour, a few examples are:
| 15 minutes | =\frac{1}{4} hour |
| 30 minutes | =\frac{1}{2} hour |
| 45 minutes | =\frac{3}{4} hour |
Time Formats
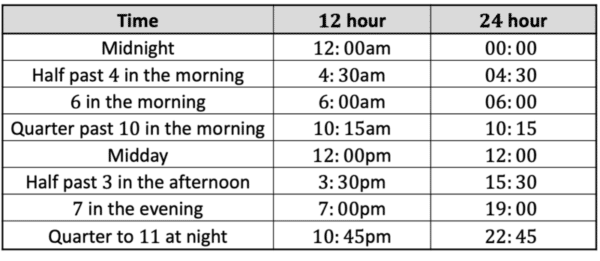
Times of the day can be displayed by either a \textcolor{blue}{12} hour clock, or a \textcolor{red}{24} hour clock.
\textcolor{blue}{12} hour clocks show times between 12 am (midnight) and 12 pm (midday).
\textcolor{red}{24} hour clocks show times between 00:00 (midnight) and 23:59 (one minute to midnight the next day), with 12:00 being midday.
For example, here are some comparisons between a \textcolor{blue}{12} and \textcolor{red}{24} hour clock:
Hint: if you are given a time in the afternoon in \textcolor{red}{24} hour format, subtract 12 hours to tell the time.
For example, 16:00 subtract 12 hours is 4:00, so we know this is 4 in the afternoon.
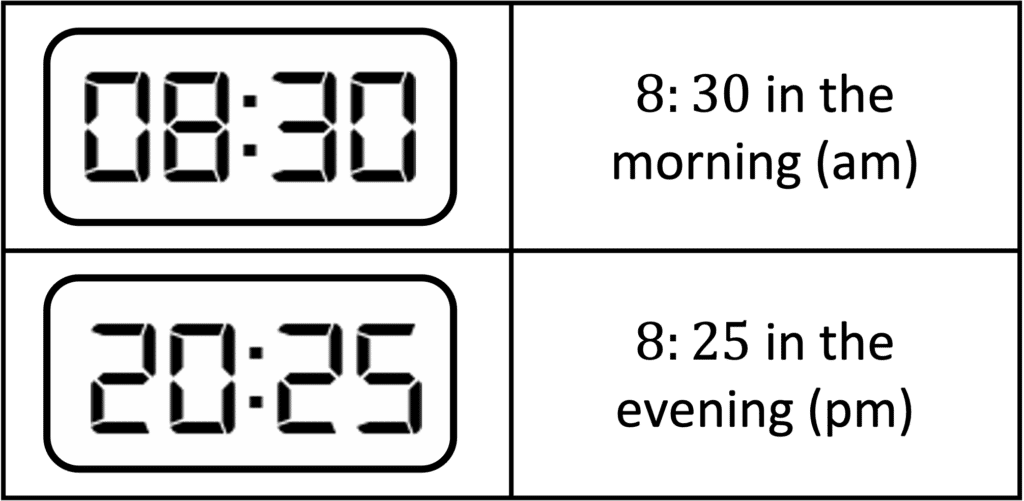
Digital Clocks
Digital clocks usual show time in \textcolor{red}{24} hour format, and they are easy to understand.
The digits before the colon represent the hour, and the digits after the colon represent the minutes.
Analogue Clocks
Analogue clocks usually show time in \textcolor{blue}{12} hour format, and they are more difficult to understand.
The shorter hand represents the hour, and the longer hand represents the minutes.
Hours:
The short hand is points to the hour. If it is pointing at 10, we know it is 10 o’clock.
From an analogue clock, it is impossible to tell whether this time is in the morning or afternoon.
Minutes:
For minutes, we use the longer hand.
We know there are 60 minutes in an hour, and as analogue clocks are split into 12 sections (between each number), each section represents 5 minutes.
For example, the gap between the 12 and 1 on the clock represents 5 minutes.
We start the clock at 12, and when the longer hand is pointing at 12 we know this is 0 minutes. If the longer hand was pointing at 5, we can multiply this by 5 minutes to work out the minutes:
5\times5=25So, pointing at the 5 would represent 25 minutes past.
Worked example: reading an analogue clock
Hours: the shorter hand is pointing between the 7 and 8, so we know it is somewhere between 7:00 and 8:00, so the hour of the day would be 7.
Minutes: the longer hand is pointing between the 2 and 3. The 2 represents 2\times5=10 minutes, and the 3 represents 15 minutes. The hand is slightly closes to 2 than 3, so the minutes will be around 12.
Therefore, the time is 7:12.
Days of the Month
Another important thing to remember is how many days each month has.
30 days \begin{cases} \text{April}\\ \text{June}\\ \text{September}\\ \text{November}\\ \end{cases} \\
31 days \begin{cases} \text{January}\\ \text{March}\\ \text{May}\\ \text{July}\\ \text{August}\\ \text{October}\\ \text{December} \\ \end{cases}
\text{February} is unique, it has 28 days normally and 29 days in a leap year.
A leap year normally occurs once every 4 years.
Timetables
It is also important to be able to understand and use time from timetables.
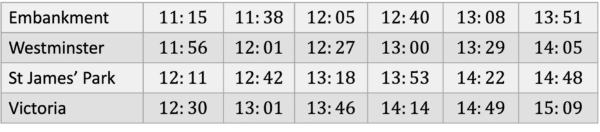
For example, here is a train timetable:
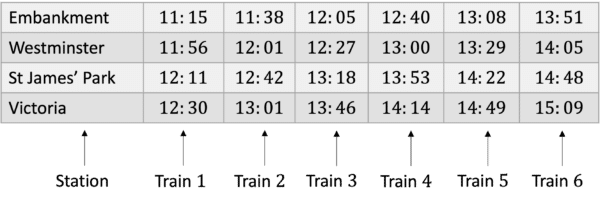
The columns represent different train services:
Solving problems with timetables:
How long would it take to get to Victoria if the 12:05 train was boarded from Embankment?
The train leaves at 12:05, and looking down the column, we can see it arrives at Victoria at 13:46.
The easiest way to calculate this is by splitting it into the 2 hours:
12:05 to 13:00 is 55 minutes.
13:00 to 13:46 is 46 minutes.
Total = 55 + 46 = 101 minutes.
We can leave this in minutes, or the question may ask us for this in hours. As there are 60 minutes in an hour:
101-60=41 minutes left.
The journey takes 1 hour and 41 minutes.
Example 1: Analogue Clocks
Helena is starting a new job. Each day, her shift will start at the time shown on Clock 1, and finish at the time shown on Clock 2. How long is her shift each day?
[4 marks]
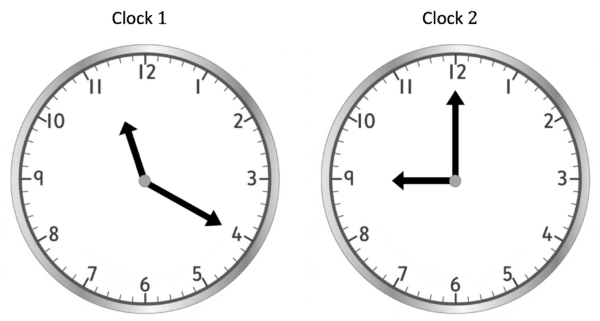
Clock 1:
Hours: 11
Minutes: pointing at 4, 4\times5=20
Time: 11:20
Clock 2:
Hours: 9
Minutes: pointing at 12, which we know is 0 minutes
Time: 9:00
So, Helena starts work at 11:20 and finishes at 9:00:
Time before 12:00 - 40 minutes
Time after 12:00 - 9 hours.
Her shift is 9 hours and 40 minutes.
Example 2: Timetables
Ellias is trying to get the bus to school. He lives by Blackfriars and his school is by Cannon Street. His school starts at 10:00 and he wants to arrive at least 10 minutes before school starts. What is the latest bus he could catch from Blackfriars
[2 marks]
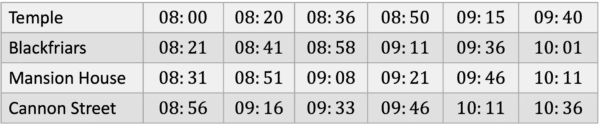
To arrive 10 minutes before school, he needs to arrive at or before 09:50 at Cannon Street.
The bus in the fourth column arrives the closest to this time, at 09:46.
Therefore, he should get the bus from Blackfriars at 09:11.
Time Example Questions
Question 1: Kim is working a 5 hour shift, starting at 1:25 pm. Find the time she will finish her shift, giving your answer using 24 hour time.
[2 marks]
Adding 5 hours on to 1:25, we get 6:25pm.
Now, to convert this to 24 hour time, we add 12 hours to the time.
6:25 + 12\text{ hours} = 18:25
Question 2: Elijah is walking to work. His work starts at quarter past 2 in the afternoon. He leaves at 13:48 and it is a 25 minute journey. Does he get to work on time?
[2 marks]
He leaves at 13:48 and it takes 25 minutes.
Splitting this into chunks, the section of his journey before 14:00, will be 60-48=12 minutes.
Remaining: 25-12=13 minutes.
He will arrive 13 minutes after 14:00, at 14:13.
His work starts at quarter past 2 pm, which is the same as 14:15.
Therefore, he will be on time.
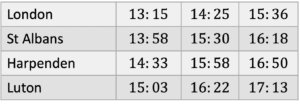
Question 3: Alana lives in St Albans. She needs to go to Luton to pick up some shopping. She does not mind what time she goes, but she wants her journey to be as fast as possible. What time should she get the train?
[4 marks]
Alana can either get the train at 13:58, 15:30, or 16:18.
13:58 train arrives at 15:03, so the time taken is:
Before 14:00, 2 minutes.
Between 14:00 - 15:00, 1 hour.
After 15:00, 3 minutes.
Total: 1 hour and 2+3=5 minutes.
1 hour and 5 minutes.
15:30 train arrives at 16:22, so the time taken is:
Before 16:00, 30 minutes.
After 16:00, 22 minutes.
Total: 30+22=52 minutes.
16:18 train arrives at 17:13, so the time taken is:
Before 17:00, 42 minutes.
After 17:00, 13 minutes.
Total: 42+13=55 minutes.
Therefore, Alana should get the 15:30 train.
