Graphical Inequalities
Graphical Inequalities Revision
Graphical Inequalities
Graphical inequalities questions involve shading a region on a graph defined by an inequality.
There are 2 types of question you may be asked, drawing graphical inequalities, and determining graphical inequalities.
In order to really understand graphical inequalities you will need to have background knowledge of the following topics:
Expressing Graphical Inequalities
The way to express a graphical inequality is as follows:
Step 1: Treat the inequality as if it were an equation.
Step 2: Plot the equation on the axes, this is done differently for > and for \leq
\leq and \geq means a solid line.
> and < means a dashed line.
Step 3: Identify which side of the line the area that satisfies the inequality is on, then shade the area
-
- If it is a greater than (or equal to) – then you shade the area above the line
- If it is a less than (or equal to) – then you shade the area below the line
Type 1: Drawing Graphical Inequalities
Shade the area that satisfies the inequality y+1 \geq 2x and mark it with the letter A.
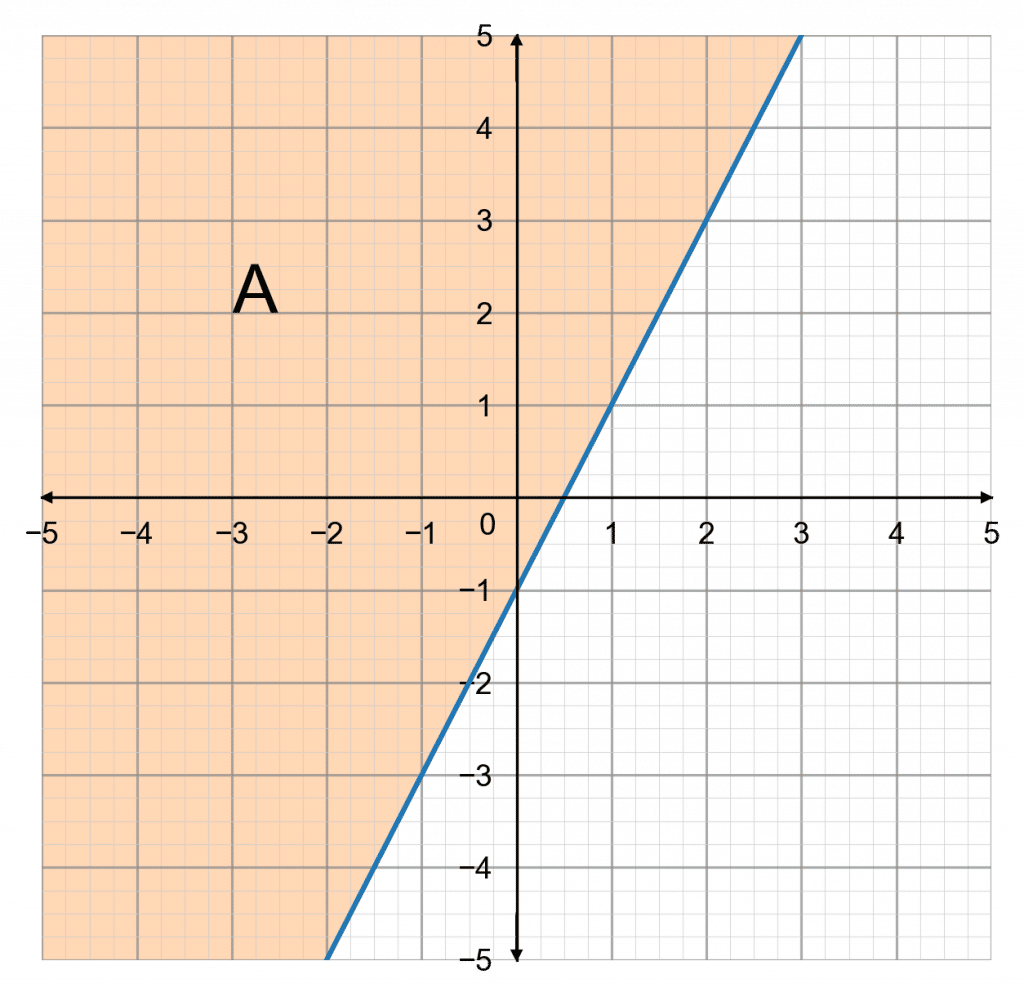

Step 1: Form the equation
Firstly rearrange the inequality, to be in the form y=mx+c.
\begin{aligned}(-1)\,\,\,\,\,\,\,\,\, y+1 &\geq 2x \\ y &\geq 2x - 1\end{aligned}
Step 2: Plot the equation
Now, we must plot y = 2x - 1 as a solid line
(as \geq means solid line)
Step 3: Shade the area above it – since it is a “greater than or equal to” – and mark that area with an A.
The result looks like the graph below.
Type 2: Determining Graphical Inequalities
Determine the 3 inequalities that describe the shaded area on the graph below.
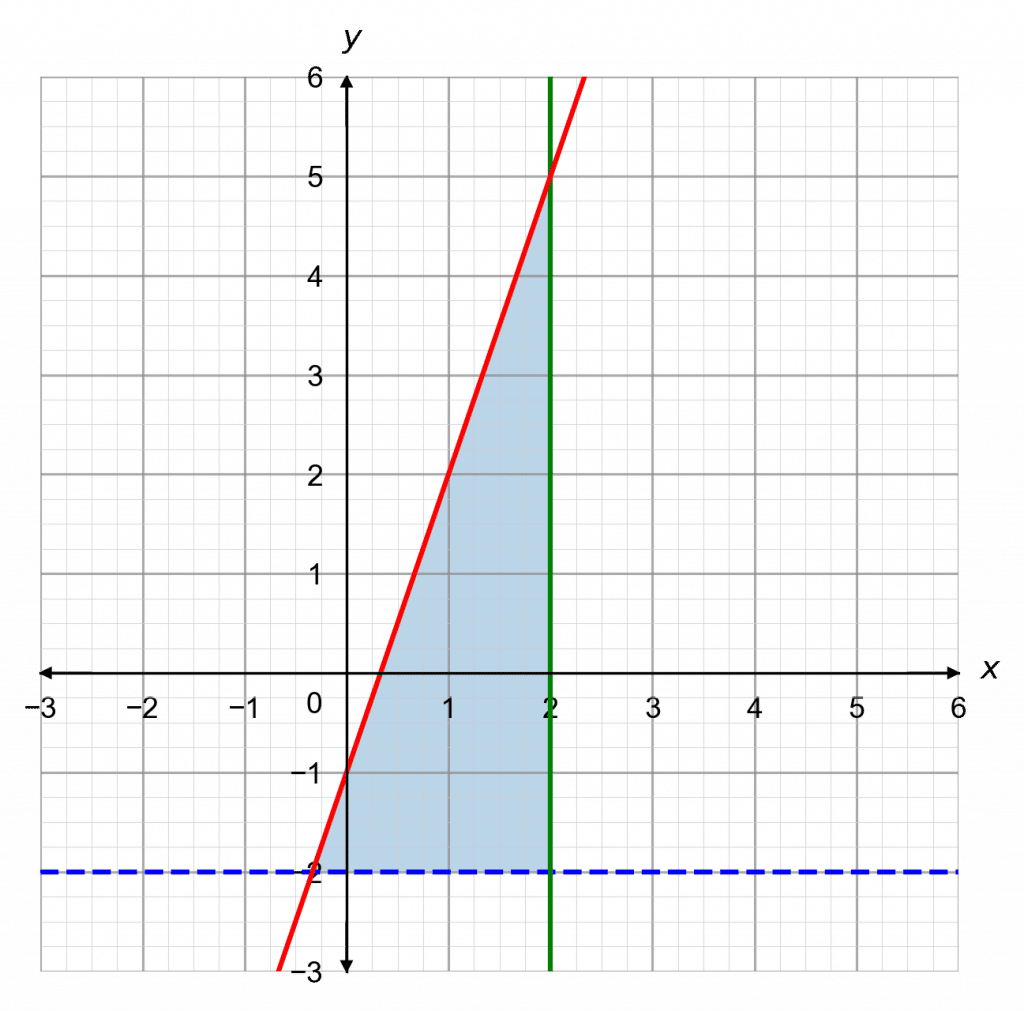

Step 1: find the equations of the 3 lines that have been drawn on this graph.
The horizontal line is y=-2
The vertical line is x=2
Then, we can see that the slanted line has a y-intercept of -1 and a gradient of 3, so its equation must be
y=3x-1
Step 2: Convert them to the appropriate inequalities.
y=-2 is dashed, the shaded area is above it, giving y>-2.
x=2 is solid and the shaded area is to the left of it, giving x\leq 2.
y=3x-1 is solid and the shaded area is below it, giving y\leq 3x-1.
So, the 3 inequalities are
y>-2,\hspace{2mm}x\leq2\text{, and }y\leq 3x-1
Example: Graphical Inequalities
Shade the region of a graph that satisfies the inequalities y>2, x\geq-1, and y < -x + 5 and mark it with an A.
[4 marks]
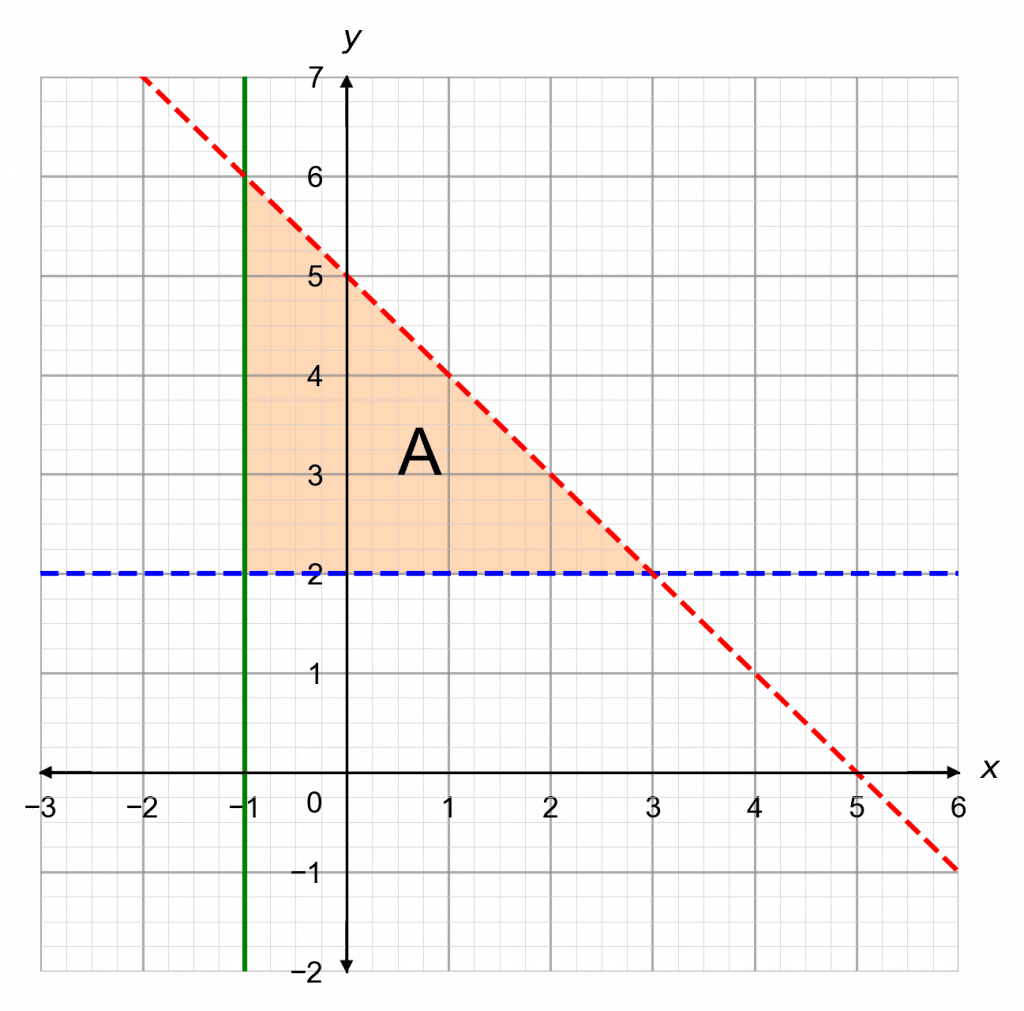

Step 1: Form the equations
y>2, becomes y = 2
x\geq-1, becomes x=-1
y<-x+5 becomes y=-x+5
Step 2: Plot the equations.
y>2, Will be dashed line
x\geq-1, Will be solid line
y<-x+5 Will be dashed line
Step 3: Identify which side of the line the area that satisfies the inequality is on, then shade the area
y>2, Will be above the line
x\geq-1, Will be above the line (to the right in this case)
y<-x+5 Will be below the line
The completed drawing, with the shaded region marked A, looks like is shown.
Graphical Inequalities Example Questions
Question 1: Shade the region of a graph that satisfies the inequality x + 2y \leq + 8 and mark it with an R.
[2 marks]
Firstly, rearrange this equation to make y the subject by subtracting x from both sides to get
2y \leq 8 - x
Then, divide both sides by 2 to get
y \leq -\dfrac{x}{2} + 4
Drawing this is an equation, the graph would be a solid line with gradient -\frac{1}{2} and y-intercept 4. Once drawn, we should shade and mark the region below the line. The result looks like:
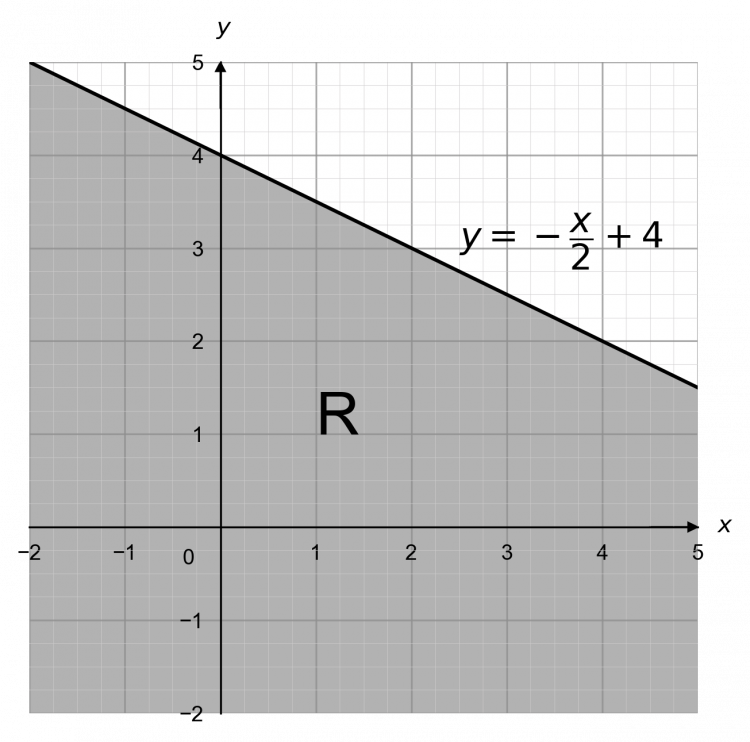
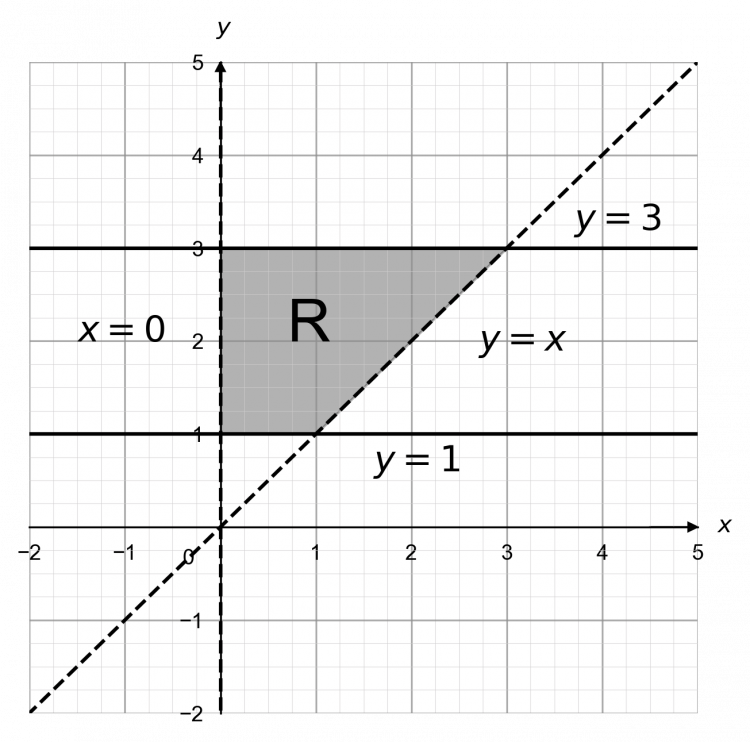
Question 2: Shade the region of a graph that is satisfied by the inequalities y \geq 1, y \leq 3, x>0, and y > x, and mark it with an R.
[4 marks]
We’re going to treat the inequalities as equations and plot them as straight lines. The first one will be the solid plot of the line y=1, the second will be a solid plot of the line y=3, the third will be a dashed plot of the line x=0, and the fourth will be a dashed plot of the line y=x.
Now, we want to shade the area that is below the line y=1, above the line y=3, to the right of the line x=0, and above the line y=x.
The resulting graph looks like:
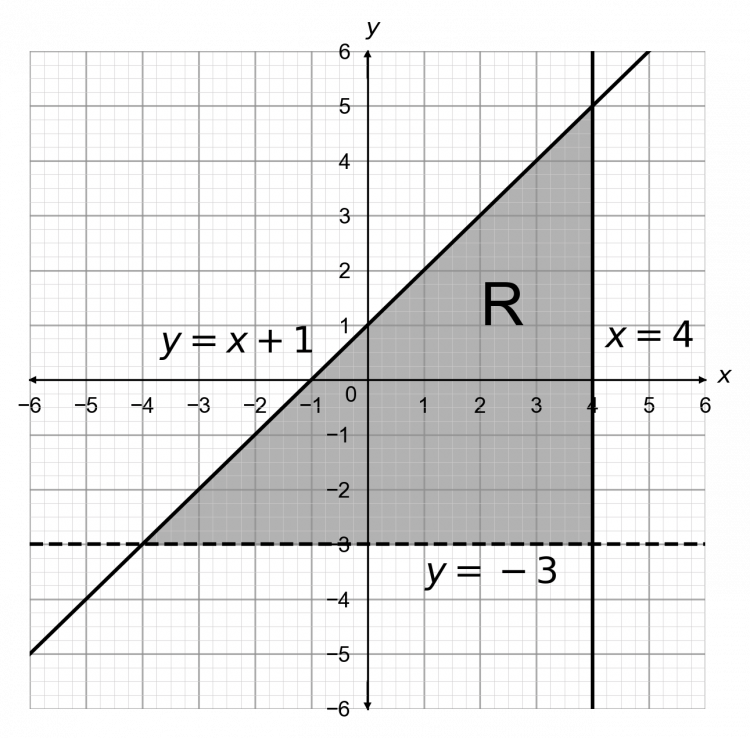
Question 3: Shade the region of a graph that is satisfied by the inequalities y \leq x+1, y >-3, and x\leq 4, and label the area with an R.
[4 marks]
We’re going to treat the inequalities as equations and plot them as straight lines. The first one will be the solid plot of the line y=x+1, the second will be a solid plot of the line x=4, and the third will be a dashed plot of the line y=3
Now, we want to shade the area that is below the line y=x+1, above the line y=-3, and to the left of the line x=4
The resulting graph looks like:
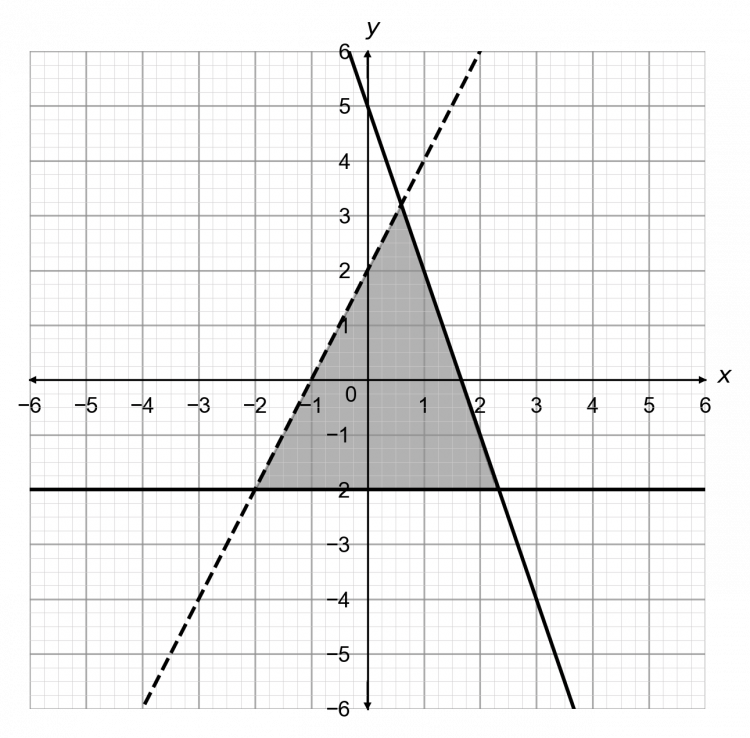
Question 4: Determine the 3 inequalities that describe the shaded area on the graph below.
[3 marks]
Firstly, determine the equations of the 3 lines and then from them, find the inequalities.
The horizontal line is clearly y = -2.
The dashed line has its y-intercept at 2 and a gradient of 2, so it is y=2x + 2
The final line has its y-intercept at 5 and a gradient of -3, so it is y = -3x + 5
Now, the shaded area is above y=-2 and the line is solid, so the inequality is
y\geq -2
The shaded area is below y=2x+2 and the line is dashed, so the inequality is
y <2x+2
The shaded area is below y=-3x+5 and the line is solid, so the inequality is
y \leq -3x+5
Therefore, the shaded area is described by the 3 inequalities
y\geq -2,\hspace{2mm} y<2x+2,\text{ and }y\leq-3x+5
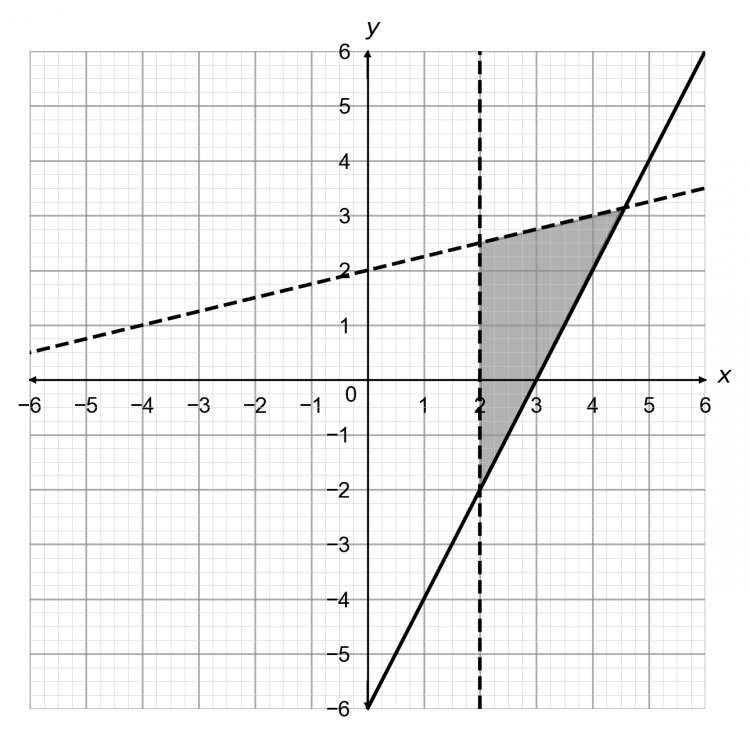
Question 5: Determine the 3 inequalities that describe the shaded area on the graph below.
[3 marks]
Firstly, determine the equations of the 3 lines and then from them, find the inequalities.
The vertical line is clearly x = 2
The dashed line has its y-intercept at 2 and a gradient of \dfrac{1}{4}, so it is y=\dfrac{1}{4}x + 2
The final line has its y-intercept at -6 and a gradient of 2, so it is y = 2x -6
Therefore, the shaded area is described by the 3 inequalities:
x> 2,\hspace{2mm} y<\dfrac{1}{4}x + 2,\text{ and }y\geq-2x -6






