Revise
Drawing Straight Line Graphs
Drawing Straight Line Graphs Revision
Drawing Straight Line Graphs
When asked to draw a straight line, there are 2 methods you can use, but it’s good to know both.
- Using a table/list of x, y coordinate values the line passes through, or
- Using the equation of the line, in the form y = mx + c.
Make sure you are familiar with the following topics before continuing:
Method 1: Table of Values Method
The table of values method involves calculating values of y for different values of x.
Example: Draw a graph for the line y = 2x - 3.
Step 1: Construct a table with suitable x values
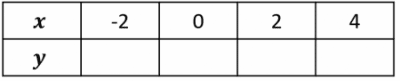
Step 2: Find the values of y for each x value.
To work out the missing values, we use the equation like a formula, substituting the values from the table in, we get the following:
When x = -2, we get y = (2\times-2) - 3 = -7
When x = 0, we get y = (2\times0) - 3 = -3
When x = 2, we get y = (2\times2) - 3 = 1
When x = 4, we get y = (2\times4) - 3 = 5
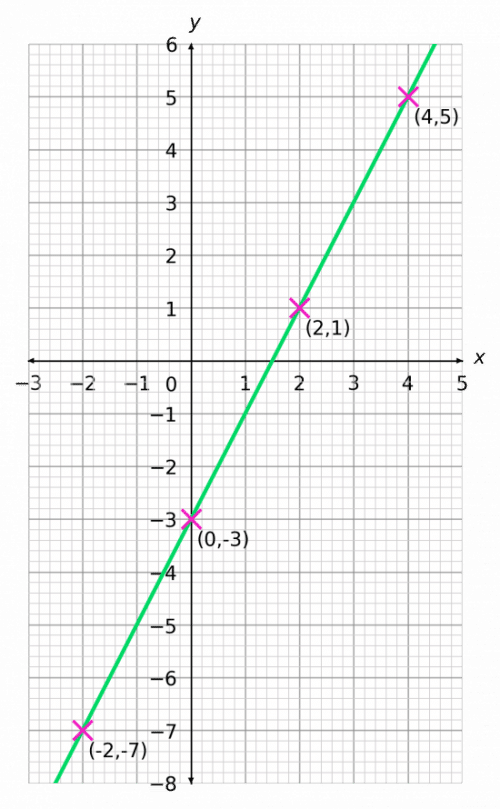
Step 3: So, we know that the line passes through
(-2, -7), (0, -3), (2, 1) and (4, 5)
Now all that remains is to plot them on a pair of axes and draw a straight line through them. The result should look like the graph below.
Method 2: Using y=mx+c
You can use y=mx+c to plot a straight line graph.
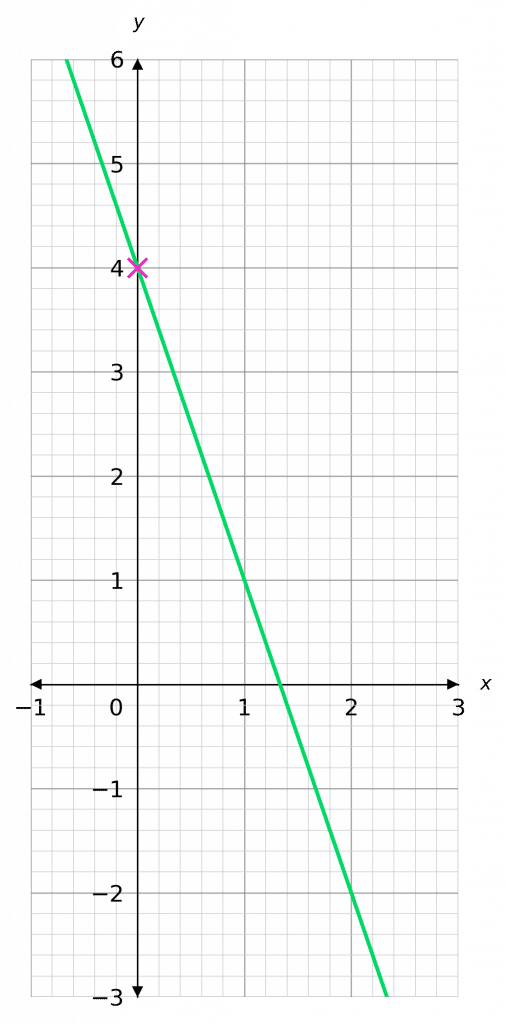
Example: Plot the straight-line graph with equation 3y + 9x = 12.
Rearranging this equation to be in the form y = mx +c, by subtracting 9x from each side
3y = -9x + 12
Then, divide both sides by 3, to get it in the form y=mx+c:
y = -3x + 4
So, the y-intercept is 4, and the gradient is -3 – so each time x increases by 1, y decreases by 3
Drawing Straight Line Graphs Example Questions
Question 1: Below is a table of coordinates of the line y = \dfrac{1}{2}x + 5. Complete the table, then plot the points and the straight-line.
[2 marks]
To find the missing value, substitute the given values into the equation.
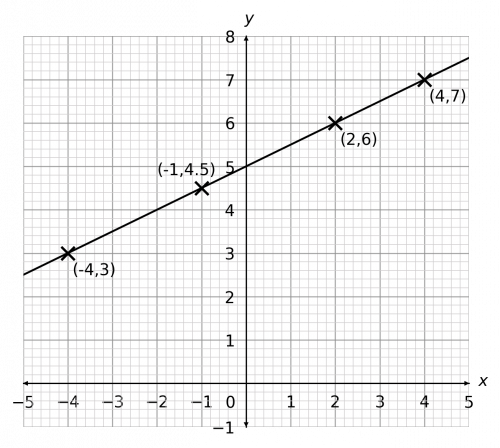
When x = -1, we get y = \dfrac{1}{2} \times (-1) + 5 = 4.5
When x = 2, we get y = \dfrac{1}{2} \times (2) + 5 = 6
When y = 7, we get 7 = \dfrac{1}{2}x + 5
Subtract 5 from both sides of this equation to get
2 = \dfrac{1}{2}x
Multiplying both sides by 2, we immediately get x = 4. The completed table looks like:
Plotting these points and using them to draw the graph should look like:
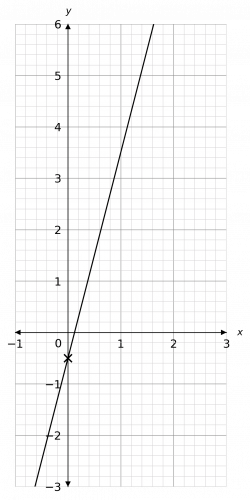
Question 2: Plot the graph of the equation 2y + 1 = 8x
[2 marks]
Let’s rearrange this equation. Subtract 1 from both sides:
2y = 8x - 1
Then, divide both sides by 2:
y = 4x - \dfrac{1}{2}
So, the y-intercept is -\frac{1}{2}, and the gradient is 4 – so each time x increases by 1, y increases by 4.
This is enough information to draw the graph. The result should look like the figure below.
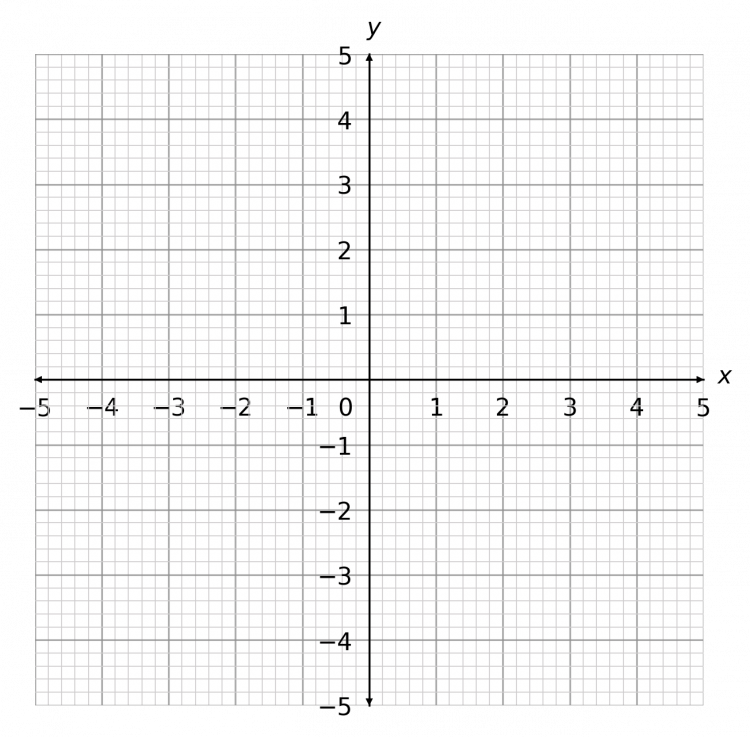
Question 3: Plot the graph of the equation y - \dfrac{1}{2} = -\dfrac{1}{2}x
[2 marks]
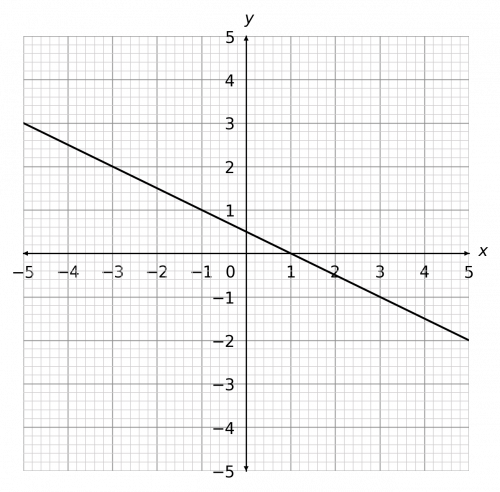
Rearranging this equation to be in the form y = mx +c, by adding 0.5 to both sides,
y = -0.5x + 0.5
So, the y-intercept is \dfrac{1}{2}, and the gradient is -\dfrac{1}{2} – so each time x increases by 1, y decreases by 0.5
The result should look like the figure below.
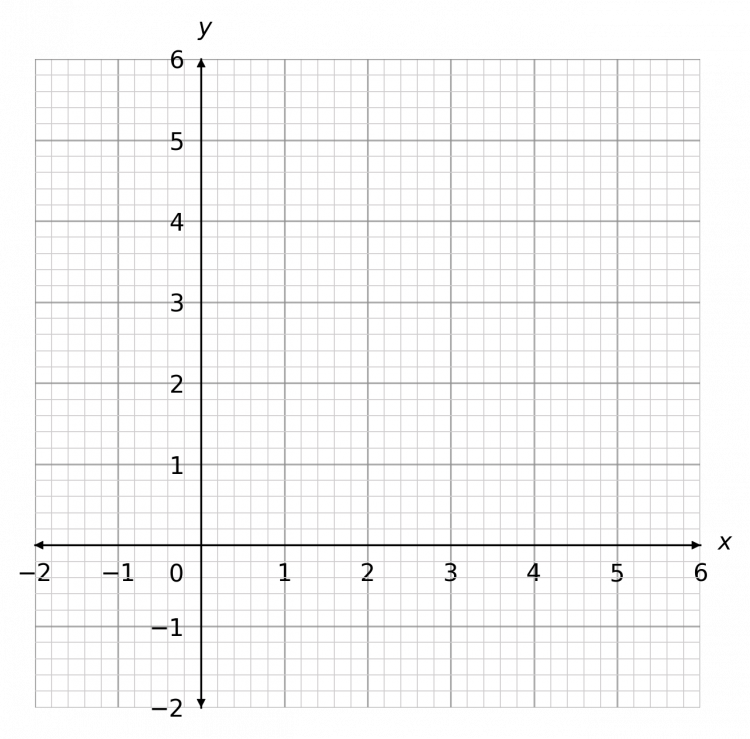
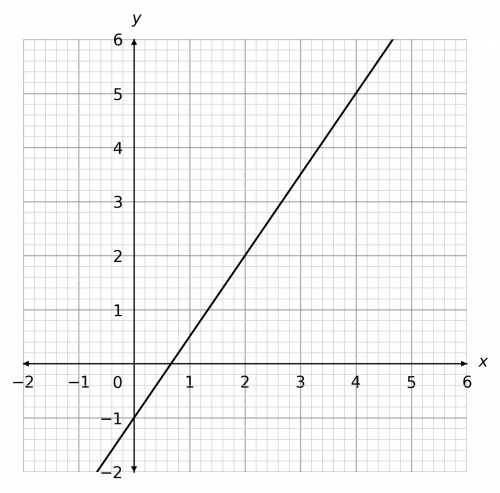
Question 4: Plot the graph of the equation 2y + 2 = 3x
[2 marks]
We can rearrange this equation by subtracting 2 from both sides:
2y = 3x - 2
Then, dividing both sides by 2:
y = \dfrac{3}{2}x - 1
So, the y-intercept is -1, and the gradient is \dfrac{3}{2} – so each time x increases by 1, y increases by 1.5
The result should look like the figure below.
Question 5: Plot the graph of the equation y + 4x +2= 0
[2 marks]
We can rearrange this equation by subtracting 4x \text{ and } 2 from both sides:
y = -4x - 2
So, the y-intercept is -2, and the gradient is -4 – so each time x increases by 1, y decreases by 4
The result should look like the figure below.
Drawing Straight Line Graphs Worksheet and Example Questions
(NEW) Drawing Straight Line Graphs Exam Style Questions - MME
Level 1-3GCSENewOfficial MMEDrawing Straight Line Graphs Drill Questions
Straight Line (2)
Level 1-3GCSE
