Parallel and Perpendicular Lines

GCSELevel 4-5Level 6-7AQACambridge iGCSEEdexcelOCRWJEC

Parallel and Perpendicular Lines Revision

Parallel and Perpendicular Lines

Parallel Lines – have the same gradient, they are always the same distance away from each other, no matter how long the lines are extended.

Perpendicular Lines – form a right-angle to each other.

Make sure you are happy with the following topics:

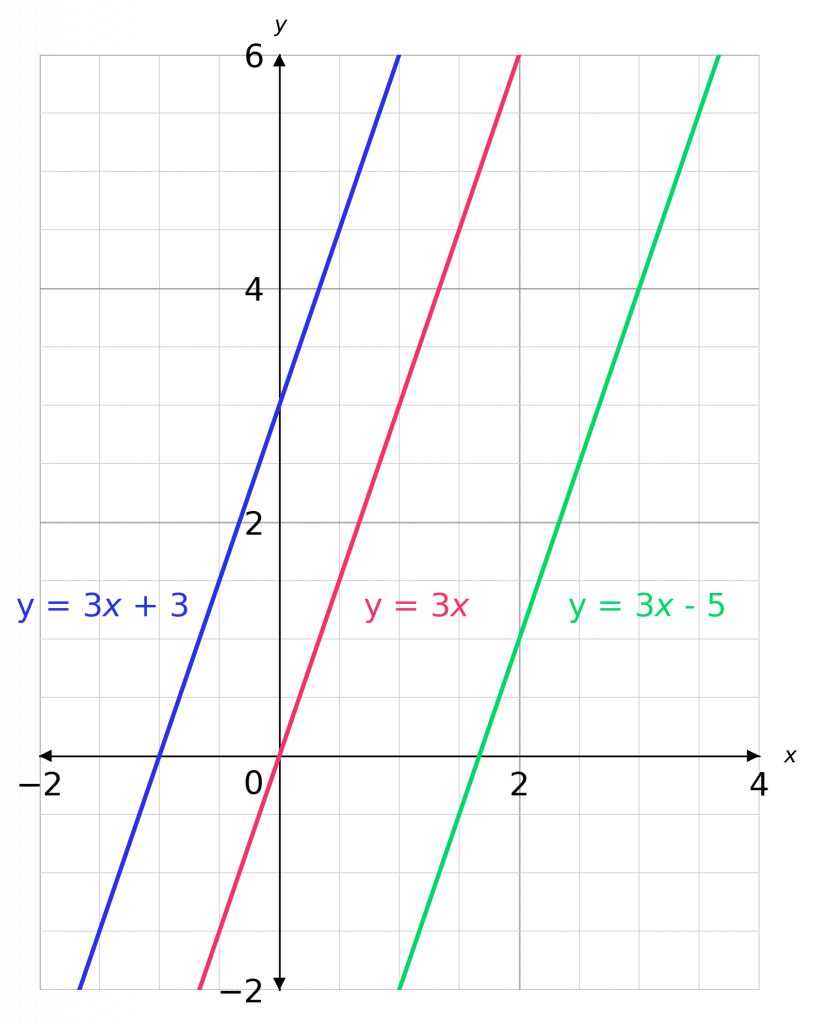
Parallel Lines – Same Gradient

Parallel lines have have the same gradient.

This will be the same $\textcolor{green}{m}$ in the straight line equation $y=\textcolor{green}{m}x+c$

For the example shown:

$y=\textcolor{green}{3}x + 3$

$y=\textcolor{green}{3}x$

$y=\textcolor{green}{3}x-5$

All three have the same gradient $\textcolor{green}{m=3}$ .

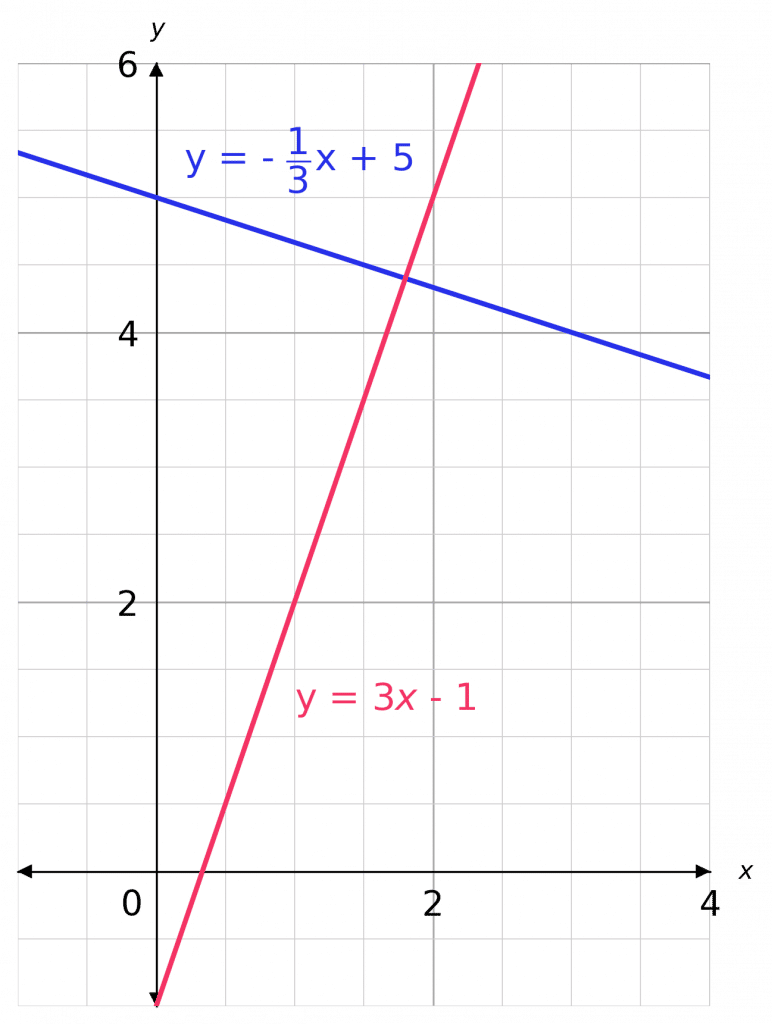
Perpendicular Lines – Right Angles

Perpendicular lines are at right angles.

When the two gradients are multiplied together the result should be $-1$

$\textcolor{green}{m} \times \textcolor{green}{-\dfrac{1}{m}} = -1$

Take a look at the example on the right:

$y = \textcolor{red}{3}x-1$

$y= \textcolor{blue}{-\dfrac{1}{3}}x+5$

If we multiply the gradients

$\textcolor{red}{3} \times \textcolor{blue}{-\dfrac{1}{3}} = -1$

So these are perpendicular.

Example: Parallel Lines

Is the line $y=3x-4$ parallel to the line $3y-9x=21$ ?

[2 marks]

We know for two lines to be parallel they need to have the same gradient $\textcolor{green}{m}$ .

First we need to get both the equations into the form $y = \textcolor{green}{m}x+c$

First line:

$y=3x-4$

This is in the correct format, we can see $m = 3$

Second line:

$3y-9x=21$

This is not in the correct format so we must first rearrange.

$3y=9x+21$ .

$y=3x+7$ .

This is now in the right form and we can see that its gradient is $3$ , so must be parallel to the $1$ st line.

Example: Perpendicular Lines

Is the line $x+4y=8$ perpendicular to the line $y=4x-13$

[2 marks]

The second line equation is in the desired form, but the first is not. So, subtracting $x$ from both sides of the first equation,

$4y = -x+8$ .

Then, dividing both sides by $4$ , we get

$y=-\dfrac{x}{4}+2$

So, the gradient of this line is $-\dfrac{1}{4}$ , and the gradient of the other line is $4$ . Multiplying these two values together, we get

$4 \times \left(-\dfrac{1}{4}\right) = -1$

Their product is $- 1$ , so the lines are perpendicular.

Parallel and Perpendicular Lines Example Questions

Question 1: State which, if any, of the following $3$ lines are parallel.

[2 marks]

a) $4y - 1 = 2x$

b) $2y + 4x = 5$

c) $y - \dfrac{1}{2}x = 45$

We need to write all $3$ equations in the form $y=mx+c$ and see which ones have the same gradient.

a) Add $1$ to both sides to get

$4y = 2x + 1$

Then, divide both sides by $4$ to get

$y=\dfrac{1}{2}x + \dfrac{1}{4}$

b) Subtract $4x$ from both sides to get

$2y = -4x+5$

Then, divide both sides by $2$ to get

$y = -2x + \dfrac{5}{2}$

c) Add $\dfrac{1}{2}x$ to both sides to get

$y=\dfrac{1}{2}x+45$

With all $3$ equations written in the desired form, we can see that whilst b) has gradient $-2$ , both a) and c) have gradient $\dfrac{1}{2}$ , therefore a) and c) are parallel.

Save your answers with

Gold Standard Education

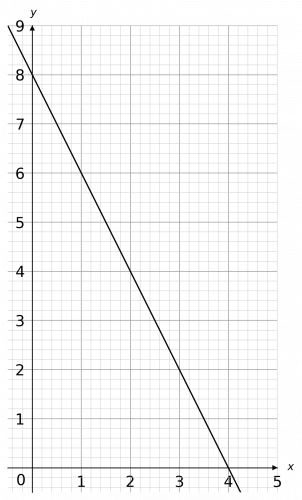
Question 2: Plot the graph, from $x=0$ to $x=4$ , of the straight line that is parallel to the line $5y=-10x-3$ and passes through the point $(1, 6)$ .

[2 marks]

We need to find the gradient of the line given in the question by writing it in the form $y=mx+c$ . Dividing both sides by $5$ , we get

$y = -2x - \dfrac{3}{5}$

Now, the line we need to draw is parallel to this one so must have the same gradient: $-2$ . We’re not asked to work out the equation (although you’re welcome to do that if it helps) and knowing that the line has gradient $-2$ and passes through $(1, 6)$ is enough to draw it. The correct plotting is shown below.

Save your answers with

Gold Standard Education

Question 3: (HIGHER ONLY) Find the equation of the line that is perpendicular to $y=\dfrac{3}{7}x+9$ and passes through the point $(5, -4)$ .

[2 marks]

The line given in the question has gradient $\dfrac{3}{7}$ . The negative reciprocal of this (and therefore the gradient of the perpendicular line) is

$-\dfrac{7}{3}$ .

Now , since we have the gradient, and we know the lines passes through $(5, -4)$ , we can substitute these values into $y=mx+c$ in order to find $c$ . So, we get

$-4 = \left(-\dfrac{7}{3}\right)\times 5+c = -\dfrac{35}{3}+c$

The most important thing here is to be careful with your fraction operations. Adding $\dfrac{35}{3}$ to both sides, we get

$\begin{aligned}c=-4+\dfrac{35}{3}&=-\dfrac{4}{1}+\dfrac{35}{3}\\ \\&=-\dfrac{12}{3}+\dfrac{35}{3}=\dfrac{23}{3}\end{aligned}$

Therefore, the equation of the line is

$y=-\dfrac{7}{3}x+\dfrac{23}{3}$

Save your answers with

Gold Standard Education

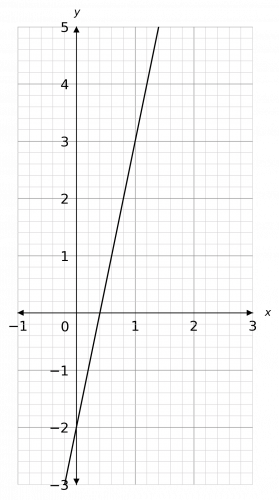
Question 4: Find the equation of the straight line that passes through $(1, 3)$ and is parallel to the line $y=5x-1$ . Plot this straight line.

[2 marks]

The gradient of the given line is $5$ , which means the gradient of the parallel line must also be $5$ . We’re given that it passes through $(1, 3)$ , and we now know the gradient to be $5$ , so we can substitute these values into $y=mx+c$ in order to find $c$ . Doing so, we get

$3 = 1\times 5 +c = 5+c$ , therefore $c =3-5=-2$ .

So, the equation of this line is

$y=5x-2$ .

We now have plenty of information to plot the graph. The result looks like the figure below.

The remainder of this topic is only relevant for the higher course.

If two lines are perpendicular, then the product of their two gradients (i.e., the result of multiplying them together) is -1. Another way of putting this is: if you have a straight line with gradient $m$ , then a line which is perpendicular to it will have gradient $-\dfrac{1}{m}$ . This is often referred to as the negative reciprocal of $m$ .

Save your answers with

Gold Standard Education

Question 5: Find the equation of the straight line that passes through $(-9, -2)$ and is perpendicular to $y=-3x+10$ . Plot the straight line.

[3 marks]

The gradient of the given line is $-3$ , so the gradient of the perpendicular line must be

$-\left(\dfrac{1}{-3}\right) = \dfrac{1}{3}$

The two minus signs cancel, so the result is a positive number. The gradient of one line and another line perpendicular to it will always have opposite signs – if one is negative the other will always be positive and vice versa.

We’re given that the line passes through $(-9, -2)$ , and we now know the gradient is $\dfrac{1}{3}$ , so we can substitute these values into $y=mx+c$ in order to find $c$ . Doing so, we get

$-2=(-9)\times\dfrac{1}{3}+c=-3+c$ , therefore $c=-2+3=1$ .

So, the equation of this line is

$y=\dfrac{1}{3}x+1$ .

We now have plenty of information to plot the graph. The result looks like the figure below.