Direct and Inverse Proportion

GCSEKS3Level 4-5Level 6-7AQAEdexcelOCRWJEC

Direct and Inverse Proportion Revision

Direct and Inverse Proportion

In maths, we say that two quantities are proportional if as one changes, the other changes in a specific way. There are two types of proportionality that you need to be familiar with, direct and inverse proportion. Make sure you are happy with the following topics before continuing.

Direct Proportionality – The Basics

If two quantities are directly proportional, then as one increases the other also increases at the same rate (proportionally), e.g. as one doubles, the other one also doubles.

Example: Jeremy uses $\textcolor{blue}{400\text{ g}}$ of flour to make $\textcolor{red}{8}$ muffins. How much flour would he need to make $\textcolor{purple}{30}$ muffins?

Step 1: Divide the amount of flour by $8$ to find the value of flour for $1$ muffin.

$\textcolor{blue}{400} \div \textcolor{red}{8} = 50$ g of flour.

Step 2: Multiply the amount of flour needed for $1$ muffin by the $\textcolor{purple}{30}$ muffins needed.

$\textcolor{purple}{30} \times 50 = 1500$ g of flour.

Inverse Proportionality – The Basics

If two quantities are inversely proportional, then as one increases the other decreases at the same rate (proportionally), e.g. as one doubles, the other one halves.

Example: $\textcolor{blue}{6}$ builders can build $\textcolor{red}{10}$ houses in $30$ months. How long would it take $\textcolor{purple}{18}$ builders to build the same number of houses?

Step 1: Multiply the number of months by the number of builders to get the time for $1$ builder.

$\textcolor{red}{10}$ houses would take $1$ builder $\textcolor{blue}{6} \times 30 = 180$ months

Step 2: Divide the time it would take for $1$ builder by the $\textcolor{purple}{18}$ builders.

$\textcolor{red}{10}$ houses would take $\textcolor{purple}{18}$ builders $180 \div \textcolor{purple}{18} = 10$ months.

Direct Proportionality – with Algebra

If two quantities, $y$ and $x$ are directly proportional, we can write

$y \textcolor{blue}{\propto} x$

This reads as ‘ $y$ is directly proportional to $x$ ‘, where ‘ $\textcolor{blue}{\propto}$ ‘ is the proportionality symbol. We can turn it into an equation by replacing $\propto$ with $= \textcolor{orange}k$ :

$y = \textcolor{orange}{k}x$

$\textcolor{orange}{k}$ tells us how $y$ and $x$ are related, and is called the ‘constant of proportionality‘. Other examples of direct proportionality for $y$ can be seen in the table.

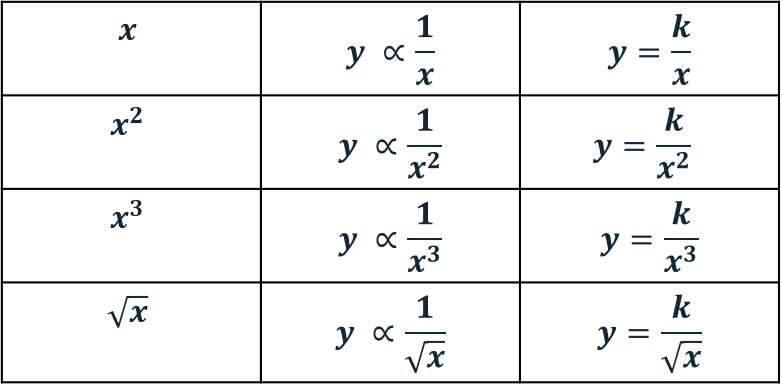
Inverse Proportionality – with Algebra

If two quantities, $y$ and $x$ are inversely proportional, we can write

$y \textcolor{blue}{\propto} \dfrac{1}{x}$

This reads as ‘ $y$ is inversely proportional to $x$ ‘, where ‘ $\textcolor{blue}{\propto}$ ‘ is the same proportionality symbol as before. We again turn this into an equation by replacing ‘ $\textcolor{blue}{\propto}$ ‘ by ‘ $= \textcolor{orange}{k}$ ‘:

$y = \dfrac{\textcolor{orange}{k}}{x}$

Other examples of inverse proportionality for $y$ can be seen in the table.

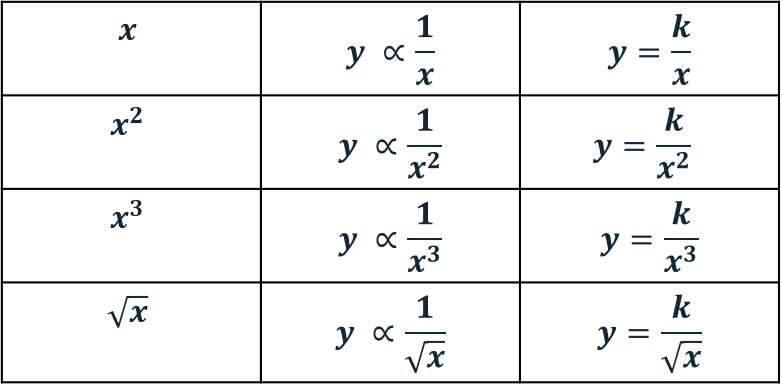
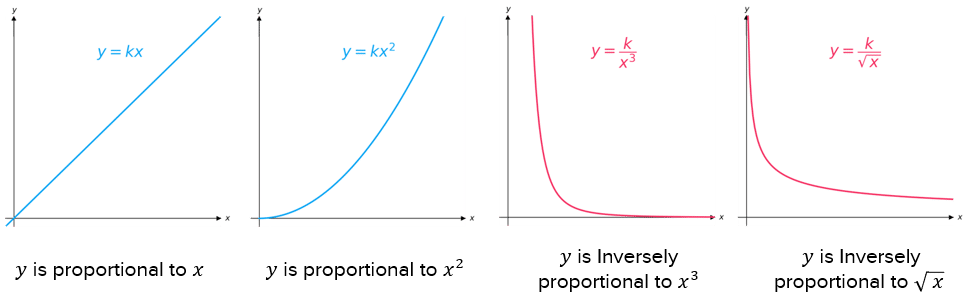
Proportionality graphs

Once we convert the proportion into an equation, we can plot a graph easily.

Note: If you are a foundation student, you won’t explicitly be asked to form an equation. However, you will be expected to know how to work with constants of proportionality and use these equation, so all of this content is still important to you.

Example 1: Direct Proportion With Equation

The force acting upon an object can be modelled by the following equation:

$F=ma$

a) The force on an object is increased from $20\text{ N}$ to $120\text{ N}$ . If the mass of the object stays the same, find the factor by which the acceleration changes.

b) The acceleration of an object is decreased from $4\text{ m/s}^{-2}$ to $2\text{ m/s}^{-2}$ . If the original force was $8\text{ N}$ , find the new force, and the mass of the object.

[5 marks]

a) Since the mass stays the same, the force is directly proportional to the acceleration.

The force increases by a factor of $120\div20=6$ , so the acceleration must increase by a factor of $6$ also.

b) Again, force and acceleration are in direct proportion. The acceleration is decreased by a factor of $4\div2=2$ , so the force must be decreased by the same factor.

F=8\div2=4\text{ N}

The mass of the object can be found by substituting in the original values: $8=4m$

Hence, $m=2\text{ kg}$

Example 2: Inverse Proportion With Equation

The number of painters painting a house is inversely proportional to the time taken to complete it. Where number of painters is $P$ , and the time taken in hours is $t$ , and some constant $k$ ,

$t = \dfrac{k}{P}$

It takes $4$ painters $8$ hours to paint the house.

How long would it take $8$ painters?

[3 marks]

Firstly find the constant $k$ by substituting $P = 4$ and $t = 8$ into the equation

$8 = \dfrac{k}{4}$

$k = 8 \times 4 =32$

Now we have

$t = \dfrac{32}{P}$

So if $P=8$

$t = \dfrac{32}{8} = 4$

It will take $8$ painters $4$ hours to finish the house.

Example 3: Direct Proportion Setting Up Equation

$y$ is directly proportional to $x$ . When $y = \textcolor{red}{24}, x = \textcolor{blue}{8}$ . Work out the value of $y$ when $x = \textcolor{blue}{2}$ .

[3 marks]

Step 1: We have that $y$ is directly proportional to $x$ , i.e. $y \propto x$ . Then, expressing this as an equation we get $y = kx$

Step 2: In the question we’re given that when $y = \textcolor{red}{24}, x = \textcolor{blue}{8}$ . Substituting these into the equation above, we get

$\textcolor{red}{24} = \textcolor{blue}{8} \times k$

$k = \textcolor{red}{24} \div \textcolor{blue}{8} = \textcolor{orange}3$

Thus, the proportionality equation becomes, $y = \textcolor{darkorange}{3}x$

Step 3: We can now use this to work out that when $x = \textcolor{blue}{2}$ , $y = \textcolor{darkorange}{3} \times \textcolor{blue}{2} = 6$

Example 4: Inverse Proportion Setting Up Equation

$y$ is inversely proportional to $x$ . When $y = \textcolor{red}{2}, x = \textcolor{blue}{3}$ . Work out the value of $y$ when $x = \textcolor{blue}{18}$ .

[3 marks]

Step 1: We have that $y$ is inversely proportional to $x$ , so we write $y \propto \frac{1}{x}$ . Then, expressing this as an equation we get

$y = \dfrac{k}{x}$

Step 2: In the question we’re given that when $y = \textcolor{red}{2}, x = \textcolor{blue}{3}$ . Substituting these into the equation above, we get

$\textcolor{red}{2} = \dfrac{k}{\textcolor{blue}{3}}$

$k = \textcolor{red}{2} \times \textcolor{blue}{3} = \textcolor{orange}{6}$

Thus, the proportionality equation becomes $y = \dfrac{\textcolor{darkorange}{6}}{x}$

Step 3: Therefore, when $x = \textcolor{blue}{18}$ ,

$y = \dfrac{\textcolor{darkorange}{6}}{\textcolor{blue}{18}} = \dfrac{1}{3}$

Direct and Inverse Proportion Example Questions

Question 1: Katie is baking a cake. The recipe calls for the following:

$525\text{ g}$ of flour

$475\text{ g}$ of sugar

$225\text{ g}$ of butter

$15$ eggs

Katie uses $210\text{ g}$ of flour in her cake.

Find how much of the other ingredients she uses.

[3 marks]

First, find the scale factor:

210\div525=0.4

Next, multiply the scale factor by the amounts of each ingredient.

Sugar: $475\times0.4=190\text{ g}$

Butter: $225\times0.4=90\text{ g}$

Eggs: $15\times0.4=6$ eggs

Save your answers with

Gold Standard Education

Question 2: $x$ is directly proportional to $\sqrt{y}$ .

$x=9$ when $y=36$ .

Find $y$ when $x=21$

[2 marks]

Set up equation:

\sqrt{y}=kx

Substitute values to find $k$ :

$\sqrt{36}=9k$

$9k=6$

$k=\dfrac{2}{3}$

Find $y$ using the new value of $x$ :

$\sqrt{y}=\dfrac{2}{3}x$

$\sqrt{y}=\dfrac{2}{3}\times21$

$\sqrt{y}=14$

$y=196$

Save your answers with

Gold Standard Education

Question 3: $F$ is inversely proportional to the square of $r$ .

$F = \dfrac{k}{r^2}$

When $F = 50, r = 3$ . Calculate the value of $F$ when $r = 12$ .

[3 marks]

$F$ is inversely proportional to the square of $r$ (i.e. $r^2$ ), so

$F \propto \dfrac{1}{r^2}$

We can rewrite this equation using $k$ to represent the constant of proportionality:

$F = \dfrac{k}{r^2}$

We know that when $F = 50, r = 3$ , so we can work out $k$ by substituting these known values into the equation:

$50 = \dfrac{k}{3^2}=\dfrac{k}{9}$

Since we want to work out the value of $k$ , we need to rearrange the formula to make $k$ the subject which we can do by multiplying each side by $9$ :

$k = 50 \times 9 = 450$

We can now rewrite the original equation with a value for the constant $k$ :

$F = \dfrac{450}{r^2} = \dfrac{450}{12^2} = 3.125$

Save your answers with

Gold Standard Education

Question 4: Given that $y$ is inversely proportional to $x$ , complete the following table.

[4 marks]

x and y Table

Since $y$ is inversely proportional to $x$ , we can write this as an equation, as follows:

$y \propto \dfrac{1}{x}$

We can rewrite this equation using $k$ to represent the constant of proportionality:

$y = \dfrac{k}{x}$

From the table, we know that when $x = 4, y = 7.5$ . If we substitute these values into our equation, we can work out the value of the constant $k$ .

Since

$y = \dfrac{k}{x}$

then

$7.5 = \dfrac{k}{4}$

Since we want to work out the value of $k$ , we need to rearrange the formula to make $k$ the subject which we can do by multiplying each side by $4$ :

$\begin{aligned} k &= 7.5 \times 4 \\ k &= 30 \end{aligned}$

We can now rewrite the original equation with a value for the constant $k$ :

$y = \dfrac{30}{x}$

Now that we have calculated the value of the constant $k$ and rewritten the original proportionality equation, we can work out the value of $y$ when $x = 60$ :

When $x = 60, y= \dfrac{30}{60} = 0.5$

We can also work out the value of $x$ when $y = 12$ :

When $y = 12$ , $12 = \dfrac{30}{x}$

If we multiply both sides by $x$ and divide both sides by $12$ , we have rearranged the equation making $x$ is the subject:

$x = \dfrac{30}{12} = 2.5$

Therefore when $y = 12, x = 2.5$

So, the completed table should look like this:

Save your answers with

Gold Standard Education

Question 5: The amount of money earned by Sasha, $M$ , is directly proportional to the number of hours she works, $h$ . If she works for $9.5$ hours she earns $£155.80$ .

a) Express $M$ in terms of $h$ .

b) Using the equation formed in part a), or otherwise, find out how many hours it would take her to earn $£688.80$ .

[4 marks]

a) Since $M$ is directly proportional to $h$ , we can write this as an equation, as follows:

$M \propto h$

We can rewrite this equation using $k$ to represent the constant of proportionality:

$M = kh$

We know that when $M = \pounds155.80, h = 9.5$ hours, so we can work out $k$ by substituting these known values into the equation:

$155.80 = k \times 9.5$

Since we want to work out the value of $k$ , we need to rearrange the formula to make $k$ the subject which we can do by dividing each side by $9.5$ :

$k = \dfrac{155.80}{9.5} = 16.4$

We can now rewrite the original equation with a value for the constant $k$ :

$M = 16.4h$

b) Now that we have calculated the value of the constant $k$ and rewritten the original proportionality equation, we can work out the value of $h$ when $M = \pounds688.80$ .

Since

$M = 16.4h$

then

$\pounds688.80 = 16.4h$

$16.4h = \pounds688.80$

then

$h = \pounds688.80 \div16.4 = 42$

So it will take Sasha $42$ hours to earn $£688.80$ .

Save your answers with

Gold Standard Education

Question 6: $x$ is directly proportional to $y$ . When $x = 2, y = 8$ .

a) Write an equation connecting $x$ and $y$

b) Calculate the value of $x$ when $y$ is $32$

c) Calculate the value of $y$ when $x$ is $50$

[6 marks]

a) $x$ is directly proportional to $y$ , so

$x \propto y$

We can therefore write this as an equation where $k$ is a constant:

$x = ky$

We now need to work out the value of the constant $k$ which we can do by substituting in the known values for $x$ and $y$ :

Since

$x = ky$

then

$2 = k \times 8$

If we make $k$ the subject of the formula by dividing both sides by $8$ , we can work out the value of $k$ :

$\dfrac{2}{8} = k$

Therefore $k$ has a value of $\frac{2}{8}$ , which can be simplified to $\frac{1}{4}$ .

Now that we know the value of the constant $k$ , we can write the equation connecting $x$ and $y$ :

Since

$x = ky$

then

$x = \frac{1}{4}y$

$x = \frac{y}{4}$

b) We now have an equation connecting $x$ and $y$ , so we can work out the value of $x$ when $y$ is $32$ .

Since

$x = \frac{y}{4}$

then

$x = \frac{32}{4}$

$32 \div4 = 8$

$x = 8$

c) We now have an equation connecting $x$ and $y$ , so we can work out the value of $y$ when $x$ is $50$ .

Since

$x = \frac{y}{4}$

then

$y = x \times 4$

$50 \times 4 = 200$

$y = 200$

Save your answers with

Gold Standard Education

Question 7: The time taken ( $t$ ) for customers to receive their orders at a fast-food restaurant is inversely proportional to the square of the number of staff ( $s$ ) on duty. It takes $20$ minutes for customer orders to be taken when there are $4$ staff members on duty.

a) Write an equation for $t$ in terms of $s$

b) If the number of staff is doubled, how many times quicker will the customers receive their orders?

[4 marks]

a) Since the time taken ( $t$ ) is inversely proportional to the square of the number of staff on duty ( $s$ ), we can write a basic equation as follows:

$t \propto \dfrac{1}{s^2}$

This formula can be rewritten using $k$ as a constant that connects $t$ and $s$ :

$t = \dfrac{k}{s^2}$

We can now work out the value of $k$ if we substitute in the known values for $t$ and $s$ :

Since

$t = \dfrac{k}{s^2}$

then

$20 = \dfrac{k}{4^2}$

$20 = \dfrac{k}{16}$

To work out the value of $k$ , we need to rearrange the formula, making $k$ the subject. We can do by multiplying both sides by $16$ :

$20 \times 16 = k$

$k = 320$

Since we now know the exact value of $k$ , we can rewrite the proportionality formula:

Since

$t = \dfrac{k}{s^2}$

then

$t = \dfrac{320}{s^2}$

b) It would be too easy to assume that if you double the staff, then the time taken would be halved! Sadly, this is not the case.

If the number of staff is doubled, then there would be $8$ staff members on duty instead of $4$ . We know from part a) that $k = 320$ and we know that $s = 8$ . If we substitute these values into our formula, it should look like this:

Since

$t = \dfrac{k}{s^2}$

then

$t = \dfrac{320}{8^2}$

$t = \dfrac{320}{64}$

$320 \div 64 = 5$ minutes

Therefore, if you double the number of staff the orders take $5$ minutes to be received instead of $20$ minutes, so the orders are received $4$ times faster.

Save your answers with

Gold Standard Education