Corresponding Angles and Alternate Angles

GCSEKS3Level 4-5AQACambridge iGCSEEdexcelEdexcel iGCSEOCRWJEC

Corresponding Angles and Alternate Angles Revision

Corresponding and Alternate Angles: 4 Simple Rules

Corresponding and alternate angles are formed when a straight line passes through two parallel lines.

Parallel means that two lines are always the same distance away from each other, and therefore will never meet. Parallel lines are marked with matching arrows as shown in the examples below.

Drawing a straight line that passes through two parallel lines creates a whole bunch of angles that are all related to each other. How these angles are related is explained by 4 simple rules.

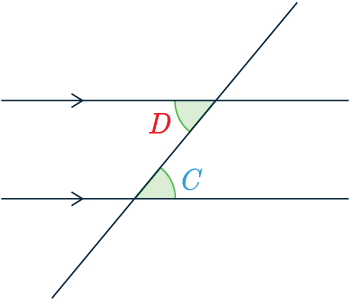
Alternate Angles:

Alternate angles are the same.

$\textcolor{red}{D} = \textcolor{skyblue}{C}$

They are found in a Z-shape, and sometimes called “Z angles“

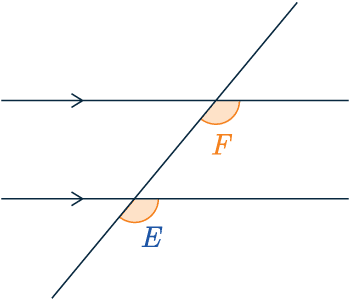
Corresponding Angles

Corresponding angles are the same.

$\textcolor{orange}{F} = \textcolor{blue}{E}$

They are found in an F-shape and are sometimes called “F angles“

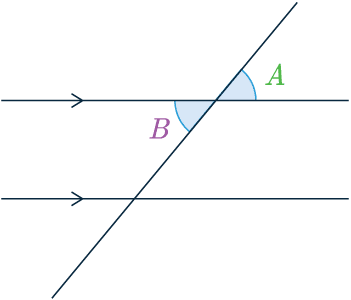
Vertically Aligned Angles

Vertically aligned angles are the same

$\textcolor{limegreen}{A} = \textcolor{purple}{B}$

These are often called “vertically opposite angles“.

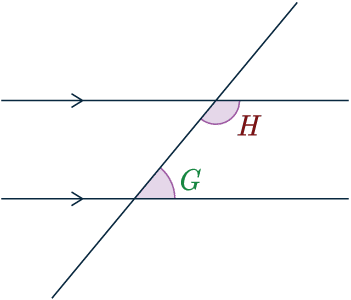
Interior / Allied angles

Allied angles add up to $180\degree$

$\textcolor{maroon}{H} + \textcolor{green}{G} = 180\degree$

These can be refereed to as either Allied angles or Interior angles.

Example: Angles in Parallel Lines

Find the angle marked $x$ in the picture below.

$BD$ and $EG$ are parallel lines.

State which angle rule you used at each step.

[2 marks]

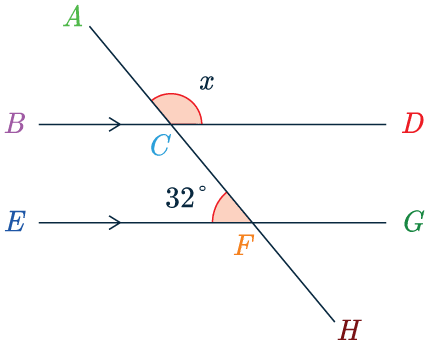
unknown alternate vertically opposite angle

Currently we cannot see a rule connecting $\angle EFC$ with $x$

This means we will need multiple steps.

Firstly, we will use the fact that angles on a straight line add to $180$ degrees.

Specifically, $\angle EFC$ and $\angle CFG$ add to make $180\degree$ .

Which means we can do the following:

$\angle CFG = 180\degree - 32\degree = 148\degree$ .

Now, looking at the diagram we can see that angle $\angle CFG$ and the missing angle $x$ are corresponding angles.

Therefore, we get

$x = 148\degree$ .

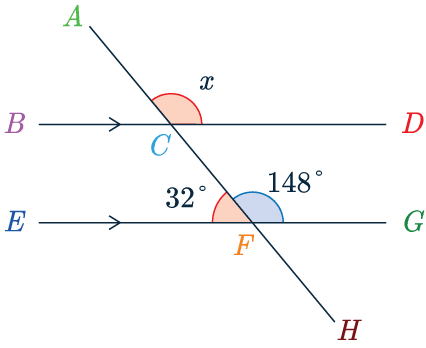
alternate unknown vertically opposite angle

As mentioned, there are multiple ways to do this question.

Corresponding Angles and Alternate Angles Example Questions

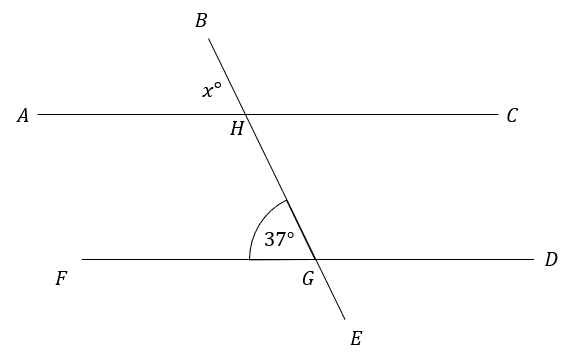
Question 1: $AHC$ and $FGD$ are parallel lines. Find the angle marked $x$ in the picture below.

State which angle rule you use at each step.

[1 mark]

unknown corresponding f angle question

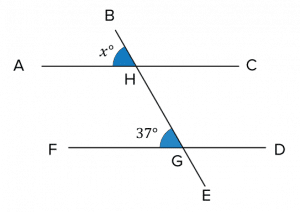
Using corresponding angles, we find that $\angle \text{AHB} = \angle \text{FGH}$ , so $\angle x = 37\degree$

Save your answers with

Gold Standard Education

Question 2: $AHC$ and $FGD$ are parallel lines. Find the angle marked $x$ in the picture below.

State which angle rule you use at each step.

[2 marks]

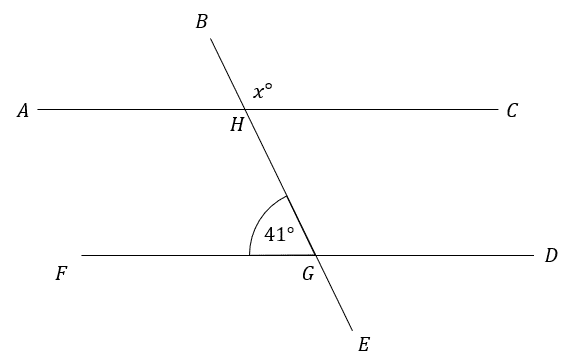
unknown interior allied vertically opposite angle question

First identifying that $\angle \text{FGH}$ and $\angle \text{GHC}$ are alternate angles, we get

$\angle \text{GHC}=41\degree$

Then as $\text{BE}$ is a straight line we can use the fact that angles on a straight line sum to $180\degree$ ,

$x=180\degree-41\degree=139\degree$

Save your answers with

Gold Standard Education

Question 3: $BD$ and $EG$ are parallel lines. Find the angle marked $x$ in the picture below.

State which angle rule you use at each step.

[2 marks]

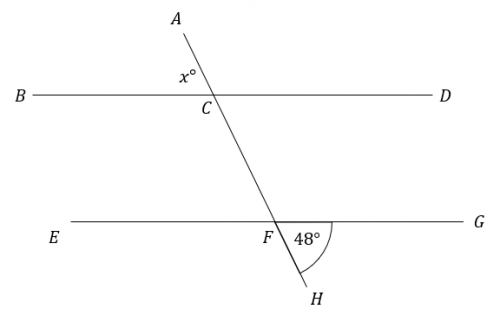
unknown vertically opposite corresponding f angle question

Firstly, because angle HFG and angle EFC are vertically opposite, we get

$\angle \text{EFC} = 48\degree$

Secondly, because angle EFC and angle BCA ( $\angle x$ ) are corresponding angles, we get

$\angle \text{BCA} = x = 48\degree$

Save your answers with

Gold Standard Education

Question 4: $AD$ and $CE$ are parallel lines. Find the angle marked $x$ in the picture below. State which angle rule you use at each step.

[3 marks]

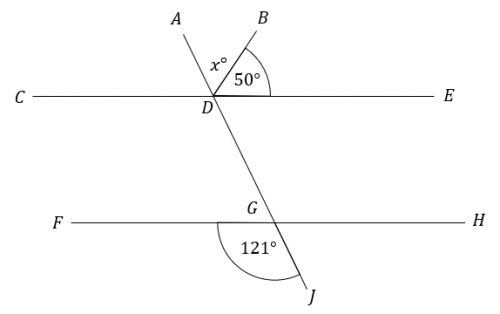
unknown angle around a point question

Firstly, using the fact that angles FGJ and CDG are corresponding angles, we get

$\angle \text{CDG } = 121\degree$

Secondly, because angles on a straight line add to $180\degree$ , and angles CDG and CDA are on a straight line,

$\angle \text{CDA } = 180 - 121 = 59\degree$

Thirdly, again using the fact that angles on a straight line add to $180\degree$ , and angles CDA, BDE, and ADB (otherwise known as angle $x$ ) are on a straight line, we get

$x + 50 + 59 = 180,\text{ so } x = 180 - 109 = 71\degree$

Save your answers with

Gold Standard Education

Question 5: $CF$ and $GI$ are parallel lines. Find the angle marked $x$ in the picture below. State which angle rule you use at each step.

[3 marks]

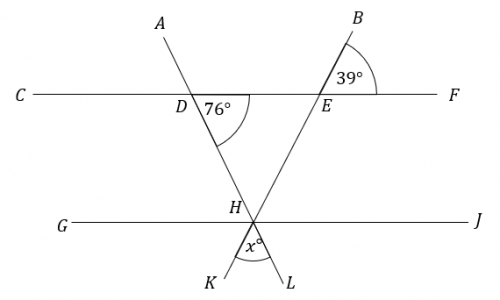
unknown angle in a triangle question

Firstly, because angles BEF and EHJ are corresponding angles, we get

$\text{angle EHJ } = 39\degree$ .

Next, because angles EDH and DHG are alternate angles, we get

$\text{angle DHG } = 76\degree$ .

Then, because angles DHG, DHE, and EHJ are angles on a straight line and angles on a straight line add to $180\degree$ , we get

$\text{angle DHE } = 180 - 76 - 39 = 65\degree$

Finally, because angle DHE and angle $x$ are vertically opposite angles, we get

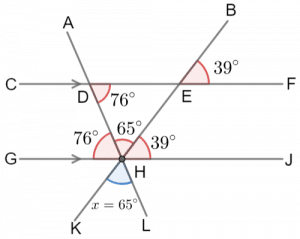
$x = 65\degree$ .

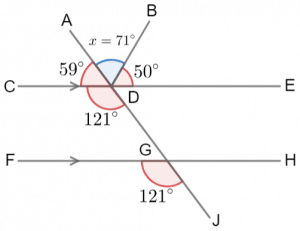
There are other possible methods for doing this question. As long as you’ve correctly applied angle fact, explained each step, and got the answer to be $71\degree$ , your answer is correct.

Save your answers with

Gold Standard Education