Circles
Circles Revision
Circles
Circles appear everywhere in maths. Mathematicians just can’t get enough of them.
Here, we’re going to introduce a few of the terms used to describe parts of a circle, and then we’re going to look at calculating the area and perimeter/circumference of a circle. The terms we’ll need are shown on the diagram and described in further detail below.
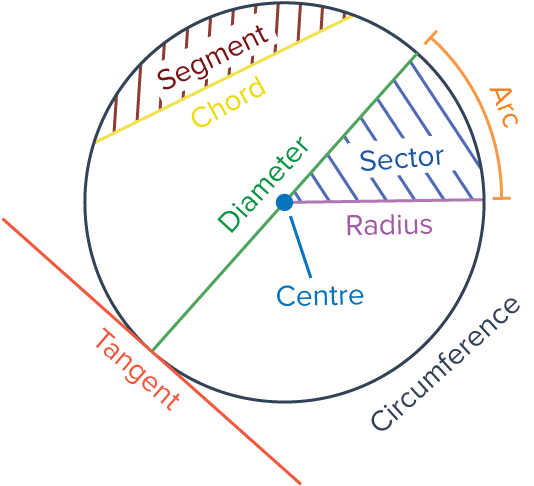
Key Circle Terms
- The circumference is the outside edge of the circle.
- A diameter is a straight line going straight through the centre of the circle and touching the circumference at each end.
- A chord is a straight line joining any two parts of the circumference.
- A segment is the area bound by the circumference and a chord.
- An arc is a section of the circumference.
- A radius (plural radii, pronounced “ray-dee-eye”) is a straight line joining the centre to the circumference.
- A sector is the area bound by two radii and an arc – like a pizza slice.
- A tangent is a straight line that touches the circumference at a single point.

Area and Circumference of a Circle
Area of a circle =\textcolor{red}{\pi} \textcolor{blue}{r}^2
Circumference of a circle =\textcolor{red}{\pi} \textcolor{green}{d} = 2\textcolor{red}{\pi}\textcolor{blue}{r}
Where \textcolor{blue}{r} is the radius, \textcolor{green}{d} is the diameter, and \textcolor{red}{\pi} is a very special number with a specific value of 3.14159265... (3.14 to 2 dp).
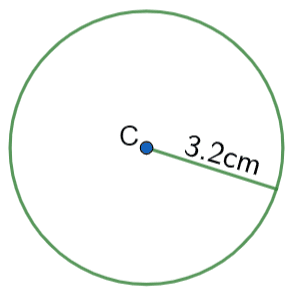
Example 1: Area of a Circle
Below is a circle with centre C and radius 3.2 cm.
Find the area of the circle to 1 dp.
[2 marks]

Formula: \text{Area }=\pi r^2.
We know the radius is 3.2, so we have
r = 3.2So, using \pi on our calculator, we get
\text{Area }=\pi \times 3.2^2=32.169...=32.2\text{ cm}^2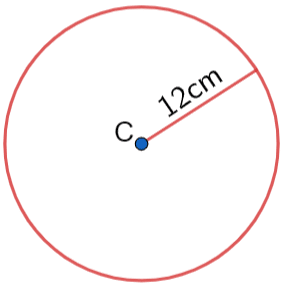
Example 2: Finding the Circumference
Below is a circle with centre C and radius 12cm.
Find the circumference of this circle.
Leave your answer in terms of \pi.
[1 mark]

Formula: \text{Circumference }=\pi d
Where d is the diameter.
We know the radius =12
So, we must double the radius to get the diameter.
\text{diameter }=2\times \text{radius}
12 \times 2 = 24
Now we can find the circumference
\text{circumference }=24\times \pi=24\pi\text{ cm}
Circles Example Questions
Question 1: Below is a circle with centre C and diameter 8.4mm.
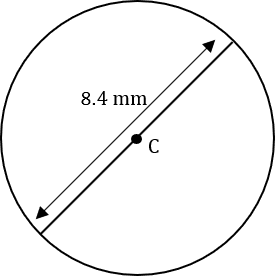
a) Find the circumference of the circle. Give your answer in terms of \pi.
[1 mark]
b) Find the area of the circle. Give your answer to 3 sf.
[2 marks]
Remember to state the units of your answers.
The formula for circumference is \pi d, so we get
\text{circumference }=\pi \times 8.4=\dfrac{42}{5}\pi\text{ mm}
The circumference is the distance around the outside, so its units are the same as those of the diameter.
b) The formula for area is \pi r^2, so firstly we have to get the radius by halving the diameter:
r=8.4\div 2=4.2
Then we get
\text{area }=\pi \times 4.2^2=55.417...=55.4\text{ mm}^2\text{ (3sf)}
Area of shapes is always measured in “squared” units. Circles are no exception.
Question 2: Calculate the area of the circle below with a radius of 5 cm, giving your answers in terms of \pi.
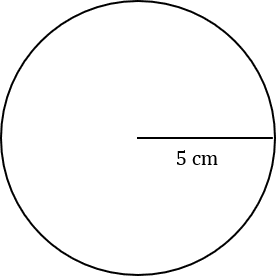
[2 marks]
Question 3: Below is a circle with centre C and radius x\text{ cm}. The area of this circle is 200\text{ cm}^2. Find the value of x to 1 dp.
[2 marks]
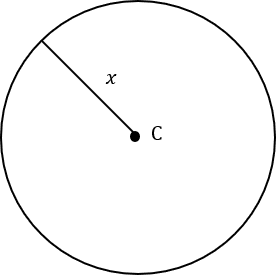
The formula for area is
\text{Area }=\pi r^2
In this case, we have \text{area}=200 and r=x. So, putting these values into the formula above, we get the equation
200=\pi x^2
We can now rearrange this equation to find x. Firstly, divide by \pi to get
\dfrac{200}{\pi}=x^2
Then, to find out the value of x, square root both sides
x=\sqrt{\dfrac{200}{\pi}}=7.97...=8.0\text{ cm (1dp)}
Question 4: Below is a circle with centre C, a circumference of 120cm and a diameter of x cm.
Find the value of x to 3 significant figures.
[2 marks]
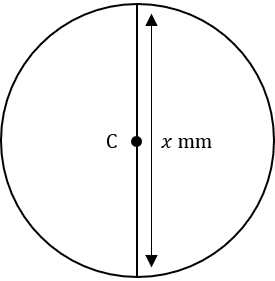
We know the formula we need is
\text{Circumference }=\pi dWe also know that the circumference is 120 and d is, in this case, x. So, filling it in those things that we have into the formula, we get
120=\pi \times xNow we have an equation we can solve. We want x, so if we divide both sides by \pi, we get
\dfrac{120}{\pi} = xPut this into a calculator and we get: x=38.2 cm, to 3sf.
Circles Worksheet and Example Questions
(NEW) Circles - The basics Exam style questions - MME
Level 1-3GCSENewOfficial MME
MME Premium Membership
£19.99
/monthLearn an entire GCSE course for maths, English and science on the most comprehensive online learning platform. With revision explainer videos & notes, practice questions, topic tests and full mock exams for each topic on every course, it’s easy to Learn and Revise with the MME Learning Portal.
Sign Up Now




