Wave Particle Duality
Wave Particle Duality Revision
Wave-Particle Duality
Sometimes in life, if we view things in a different perspective, they appear differently. Depending on how we try to observe light, sometimes we find it behaves like a wave, whilst other times it behaves like a particle. This is known as wave-particle duality or the wave-particle nature of light. In this page we look at the evidence for light acting as a wave and the evidence for its particle nature.
Light as a Wave
An experiment known as the Young’s double slit experiment can be used to show the wave nature of light. This will be discussed in much more detail in the waves unit.
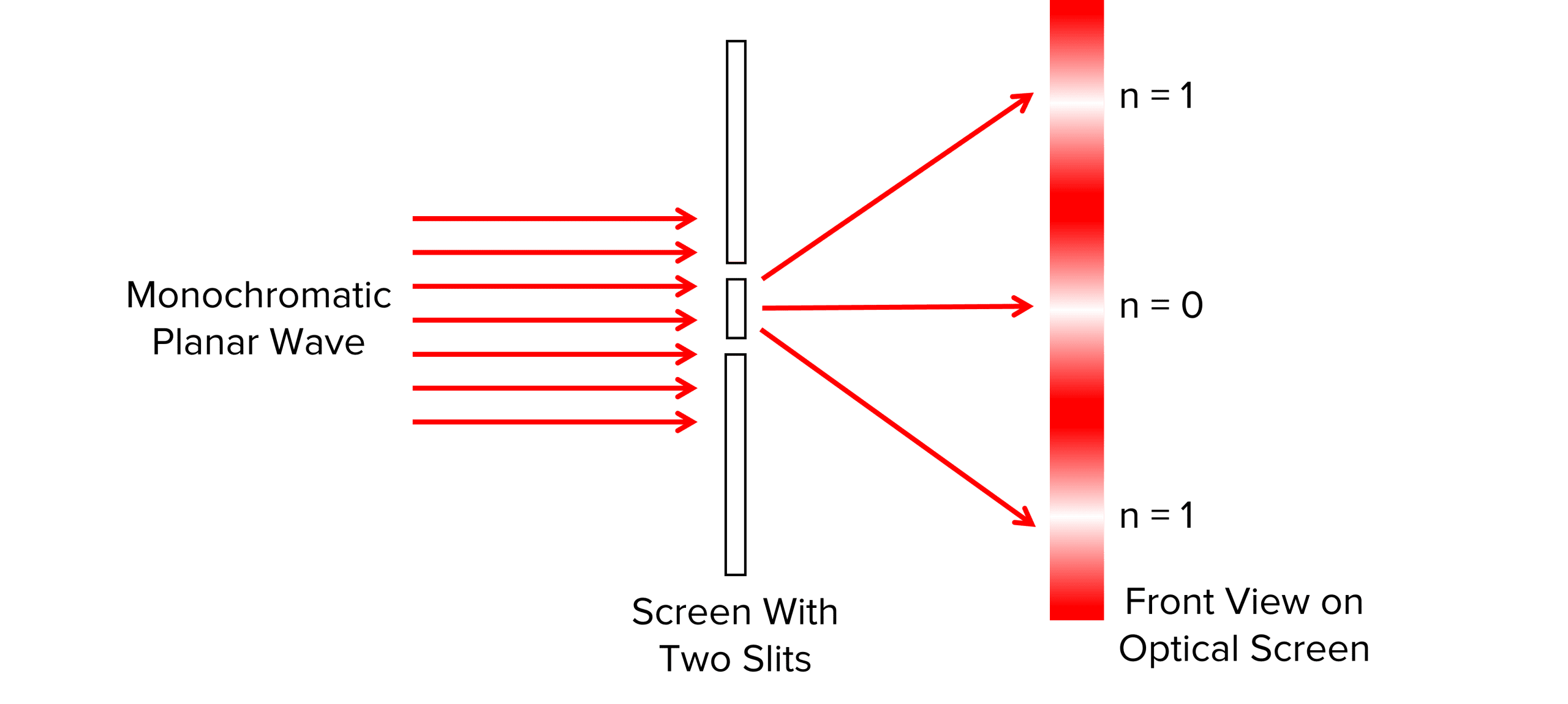
In Young’s experiment, he passed monochromatic light through two narrow slits. The light is diffracted producing a pattern as shown on the screen in the diagram above. This experiment shows light acting as a wave as this pattern is only produced when waves constructively and destructively interfere. The pattern shows a series of bright fringes (maxima) where light waves have constructively interfered, and areas of no light (minima) between the bright fringes where light waves have destructively interfered, a pattern that would not be seen if we model light as a particle.
Light as a Particle
Albert Einstein proposed that light is made up of discrete quanta of energy called photons. He described them as being packets of energy that moved like waves.
The main evidence for light being a particle is the photoelectric effect as previously discussed. The wave model of light does not support the photoelectric effect as the idea of the threshold frequency cannot work with the current model of waves. If light was to be modelled as only a wave, all frequencies of light would cause the photoelectric effect to occur, it would just take a longer exposure to the wave for low frequencies of light to cause photoelectric emission. We know this is not the case as the threshold frequency has been proven to exist.
The particle model shows that each photon either has enough energy to cause photoelectric emission or it does not. This is only true for the particle nature of waves. Increasing the intensity of light would only cause more photons to collide with the surface and therefore, more photoelectrons to be emitted. They still need to each be above the threshold frequency.
The de Broglie Wavelength
In a later experiment, Louis de Broglie investigated how particles behaved when passed through a diffraction grating (a thin piece of metal foil was used in his original experiment). The diagram for this experiment can be seen below:
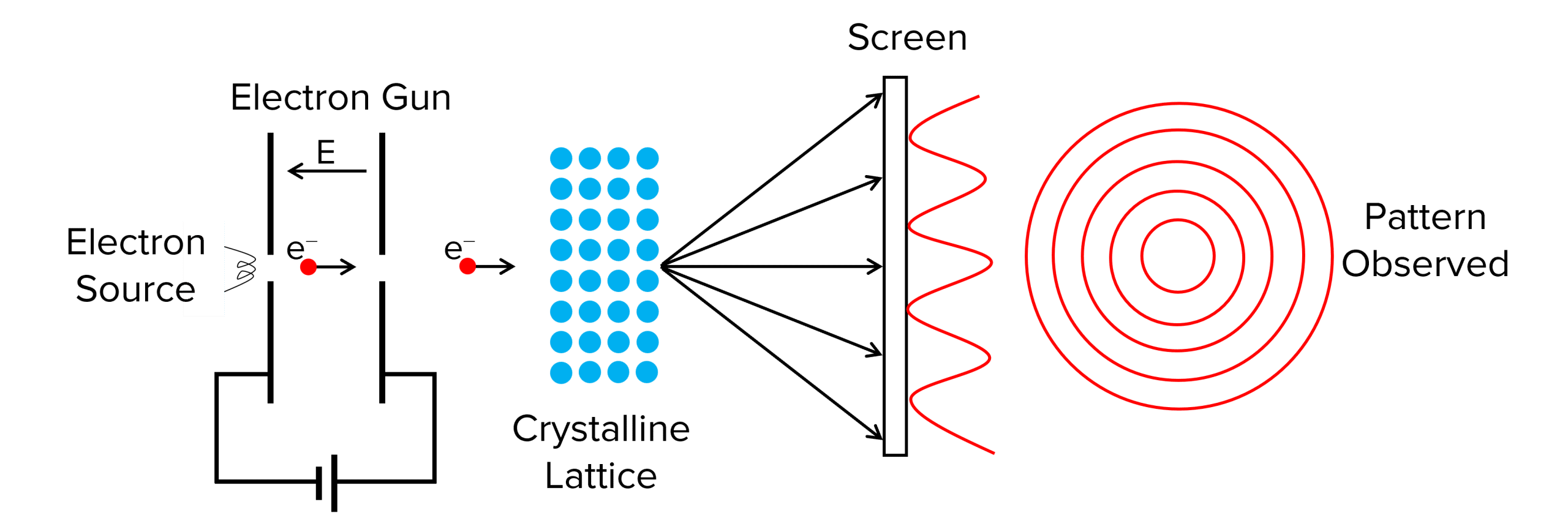
What de Broglie observed was that the electrons he fired through the grating diffracted, producing a particular pattern of concentric rings on the screen. He also observed that as the velocity of the electrons was increased, the diameter of the rings decreased.
This was enough evidence to suggest that even particles like electrons display wave-like properties and brought about the idea of wave-particle duality.
From this experiment de Broglie produced an equation linking the wavelength of a particle to its mass and velocity:
\lambda = \dfrac{h}{mv}
- \lambda= the de Broglie wavelength in metres \text{(m)}
- h= the Planck constant (6.63\times10^{-34}\text{ Js})
- mv= momentum in kilogram metres per second \text{(kgms}^{-1}\text{)}
Example: Calculating the de Broglie Wavelength
An electron is passed through a diffraction grating with velocity 2.2 \times 10^7 \text{ms}^{-1}. What is the electron’s de Broglie wavelength? (Planck’s constant = 6.63 \times 10^{-34}, Mass of electron = 9.11 \times 10^{-31})
[2 marks]
\begin{aligned} \bold{\lambda} &= \bold{\dfrac{h}{mv}} \\ \lambda &= \dfrac{6.63 \times 10^{-34}}{9.11 \times 10^{-31} \times \textcolor{aa57ff}{2.2 \times 10^7}} \\ \lambda &= \bold{3.3 \times 10^{-11}} \textbf{ m} \end{aligned}
Wave Particle Duality Example Questions
Question 1: Describe one piece of evidence that light behaves as a particle.
[2 marks]
The photoelectric effect is one piece of evidence for light behaving as a particle.
It shows that light is made of photons which either have enough energy to cause photoelectric emission, or they do not.
Question 2: Describe one piece of evidence showing that light behaves as a wave.
[2 marks]
Light can be diffracted and interference occurs.
When passed through a double slit, light produces a pattern of light (maxima) and dark (minima) fringes showing the constructive and destructive interference caused by waves.
Question 3: An electron is passed through a diffraction tube with velocity 6 \times 10^7 \text{ ms}^{-1}. What is the electron’s de Broglie wavelength? (Planck’s constant = 6.63 \times 10^{-34}, Mass of electron = 9.11 \times 10^{-31})
[2 marks]
Wave Particle Duality Worksheet and Example Questions
Quantum Phenomena Questions
A LevelOfficial MMEYou May Also Like...

MME Learning Portal
Online exams, practice questions and revision videos for every GCSE level 9-1 topic! No fees, no trial period, just totally free access to the UK’s best GCSE maths revision platform.