Progressive Waves
Progressive Waves Revision
Progressive Waves
You are likely to be familiar with progressive waves from GCSE Physics. A progressive wave transfers energy from one place to another through a medium, without transferring the medium itself.
Properties of a Progressive Wave
Here is a diagram of a progressive wave. There are several features of a progressive wave you are expected to identify and describe.
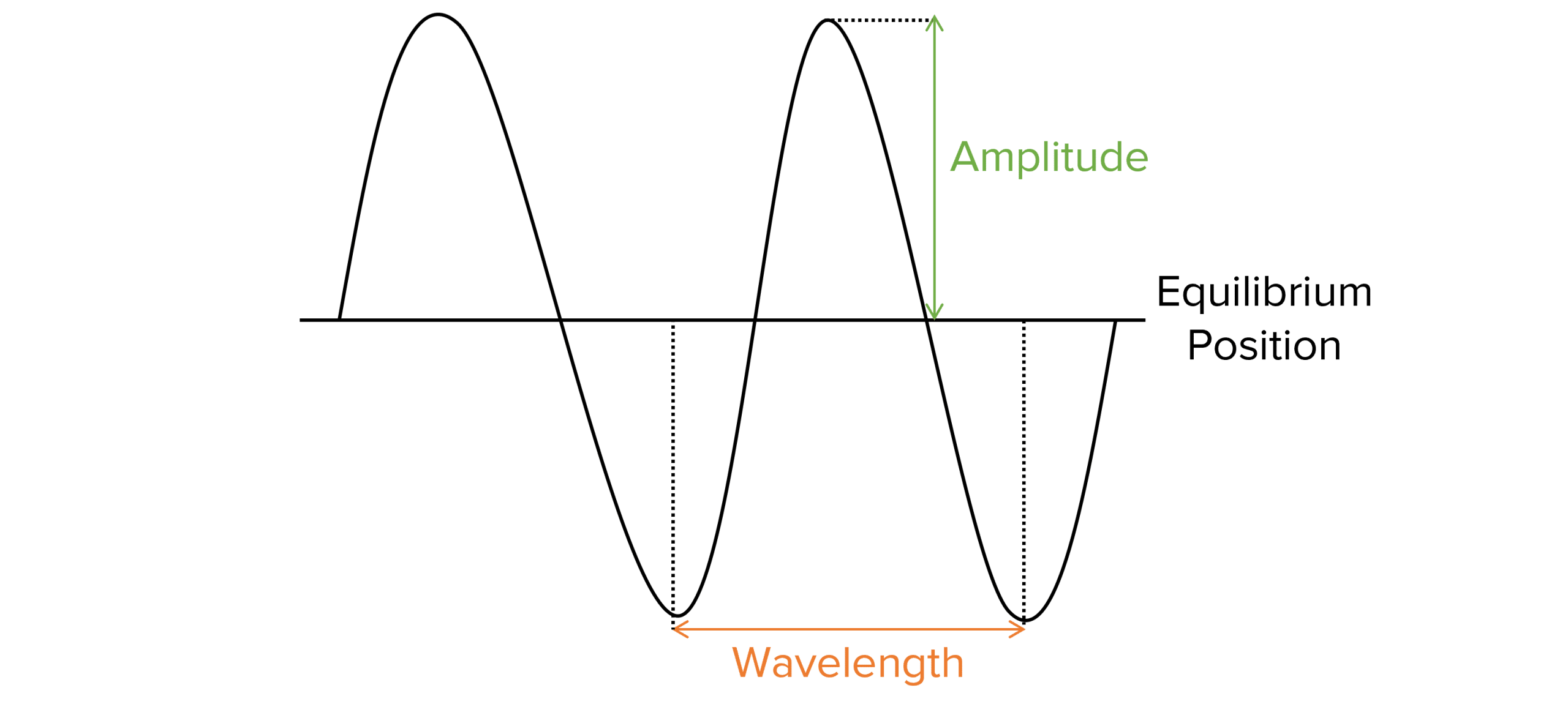
Amplitude – this is the maximum vertical displacement between the equilibrium position and the peak of the wave. We would measure this in metres.
Wavelength – this is the horizontal displacement between two identical points on the wave. On the diagram above this is represented between two peaks. Again, this is measured in metres.
Equilibrium position – the point at which the wave would form if there was zero amplitude.
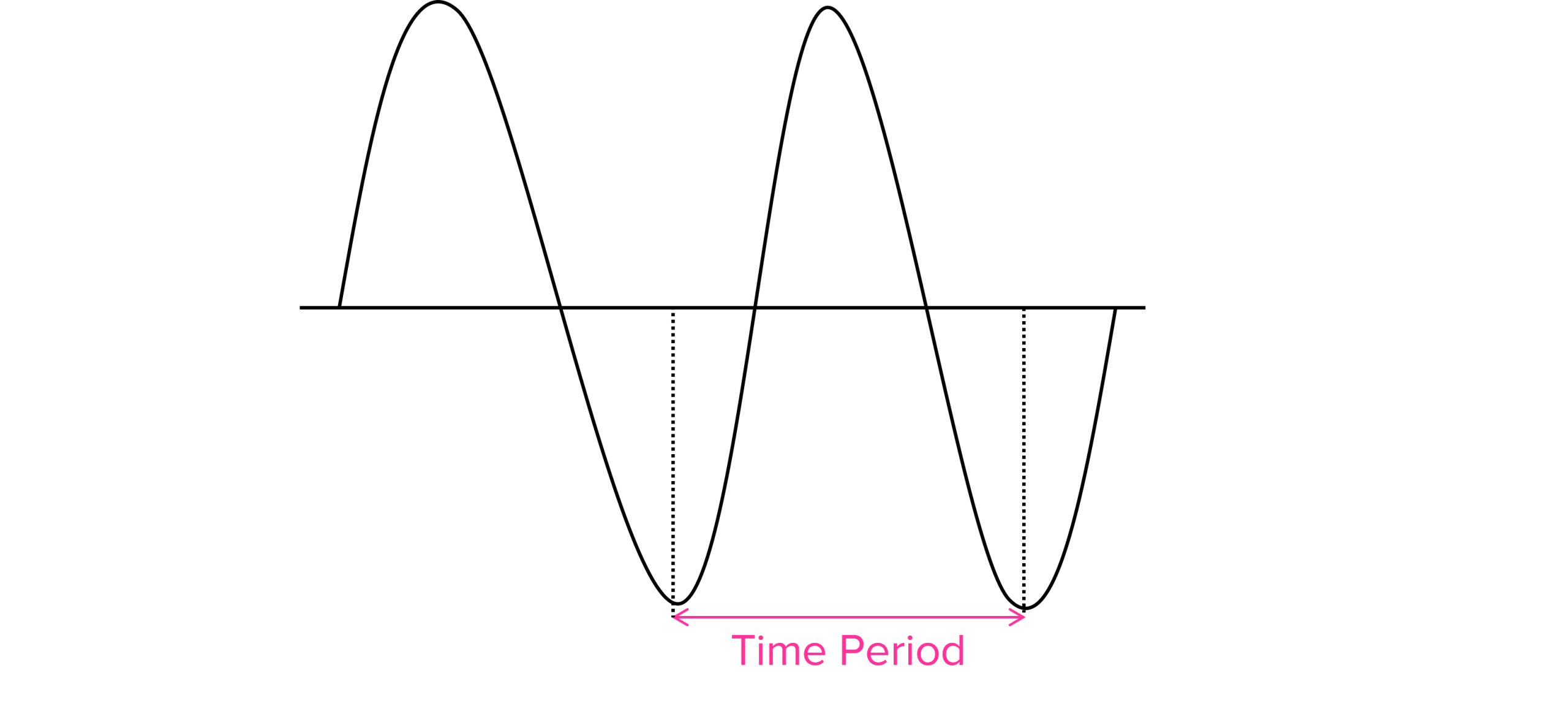
Time period – this is the time taken, in seconds, for the whole wavelength to pass a certain point.
Frequency – the frequency of a wave is related to its time period. The frequency is the number of waves that pass a given point in one second. Its units are hertz \text{Hz}, where 1 \text{ Hz} is one wave per second.
To change between time period and frequency, the following equation can be used:
f=\dfrac{1}{T}
- f= frequency in hertz \text{Hz}
- T= the time period in seconds \text{s}.
The Wave Speed Equation
This is another equation you will have come across at GCSE level but is still useful in A level physics.
v=f \lambda
- v= the wave velocity in metres per second (\text{ms}^{-1})
- f= the frequency in hertz (\text{Hz})
- \lambda= the wavelength in metres (\text{m}).
It is important to note that if we are studying any electromagnetic waves that they all travel at the speed of light and therefore, the equation can be rearranged to become:
c=f\lambda
- c= the speed of light =3\times 10^8 \text{ ms}^{-1}.
Phase Difference
Waves from a source may not always reach an object at the same time. The phase difference of two waves is a measure of how far two identical points are away from each other on two identical waves.
Here we can see two identical waves, one in red one in blue to help compare. They have the same wavelength and frequency but the red wave is slightly behind the blue wave. We say they have a phase difference.
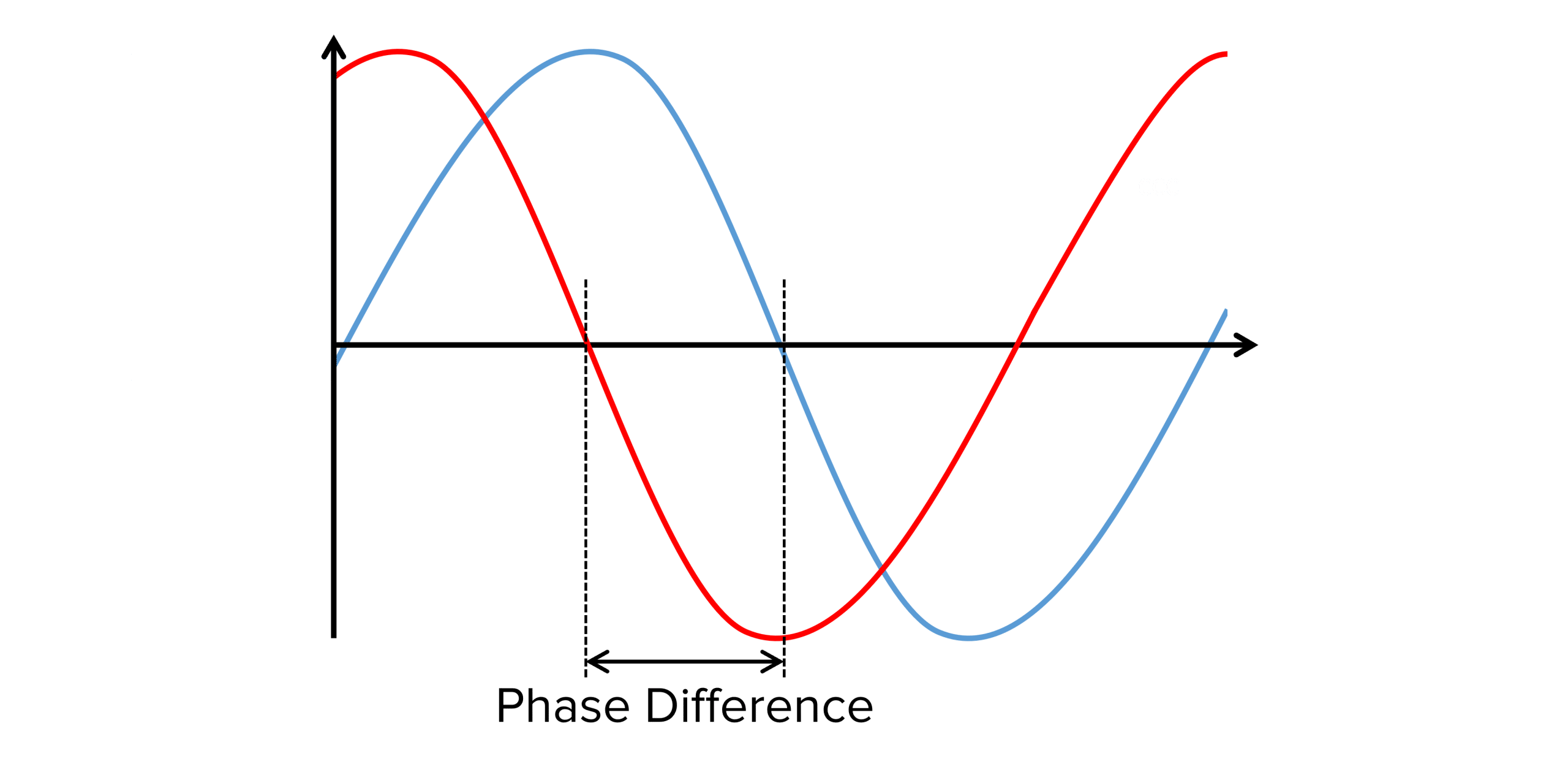
In the diagram, the blue wave is \dfrac{1}{4} of a wavelength (\dfrac{1}{4} \lambda ) ahead of the red wave. This can also be expressed in terms of degrees or radians.
To convert to degrees, we multiply the fraction of the wavelength by 360 degrees. So, for the example in the diagram::
\dfrac{1}{4} \times 360 = \bold{90 \degree}
So the two waves are out of phase by 90 degrees.
Alternatively, we can convert to radians by multiplying the fraction of the wavelength by 2 \pi. For the example in the diagram this is:
\dfrac{1}{4} \times 2 \pi = \bold{\dfrac{\pi}{2}} \textbf{rad}
If two waves are exactly 360 \degree \text{ or } 2\pi \text{ rad} (or multiples of this) out of phase, then the peaks and troughs of the waves will line up. In this case we say that the two waves are in phase.
If the waves are exactly 180 \degree \text{ or } \pi \text{ rad} out of phase, then the two waves are said to be in anti-phase.
Example 1: Calculating Time Period of a Wave
The frequency of red light is 480 \text{ THz}. What is the time period of a wave of red light?
[1 mark]
\begin{aligned} T &=\dfrac{1}{f} \\ &= \dfrac{1}{\textcolor{d11149}{480 \times 10^{12}}} \\ &= \bold{2.1 \times 10^{-15}} \textbf{ s} \end{aligned}
Example 2: Calculating Wavelength Using the Wave Equation
Calculate the wavelength of a wave of red light with frequency 480 \text{ THz}.
[2 marks]
Light is an EM wave therefore we use:
c=f \lambda
Rearrage to make wavelength the subject:
\begin{aligned} \lambda &= \dfrac{c}{f} \\ &= \dfrac{3 \times 10^8}{\textcolor{ffad05}{480 \times 10^{12}}} \\ &= \bold{6.25 \times 10^{-7}} \textbf{ m or } \bold{625} \textbf{ nm} \end{aligned}
Progressive Waves Example Questions
Question 1: A wave has a measured time period of 0.01 \text{ s}. Calculate its frequency.
[1 mark]
\begin{aligned} f&=\dfrac{1}{T} \\ &= \dfrac{1}{0.01} \\ \\ &= \bold{100} \textbf{Hz} \end{aligned}
Question 2: The above wave from Question 1 has a wavelength of 400 \text{ nm}. Calculate the speed of the wave.
[1 mark]
\begin{aligned} v &=f \lambda \\ &= 100 \times 400 \times 10^{-9} \\ &= \bold{4 \times 10^{-5}} \textbf{ ms} \bold{^{-1}} \end{aligned}
Question 3: Two waves are out of phase by \dfrac{1}{3} of a wavelength. What is their phase difference in degrees and radians?
[2 marks]
\dfrac{1}{3} \times 360 \degree = \bold{120 \degree} \\ \dfrac{1}{3} \times 2 \pi = \bold{ \dfrac{2}{3} \pi}
Question 4: What is a progressive wave?
[2 marks]
A progressive wave is wave which transfers energy from one place to another.
Without transfer in matter.
Question 5: Describe what is meant by the terms, in-phase and in anti-phase.
[2 marks]
If two waves are in-phase, the peaks of each of the waves line up at the same point.
If two waves are in anti-phase, the peaks and troughs align with each other. They are exactly half a wave cycle out from one another.
You May Also Like...

MME Learning Portal
Online exams, practice questions and revision videos for every GCSE level 9-1 topic! No fees, no trial period, just totally free access to the UK’s best GCSE maths revision platform.