The Photoelectric Effect
The Photoelectric Effect Revision
The Photoelectric Effect
When light of sufficient energy shines upon a metal surface, electrons are emitted from the surface of the metal. This phenomenon is known as the photoelectric effect. As well as providing evidence for the particle nature of light, it also is the phenomenon behind solar cells.
Photoelectrons
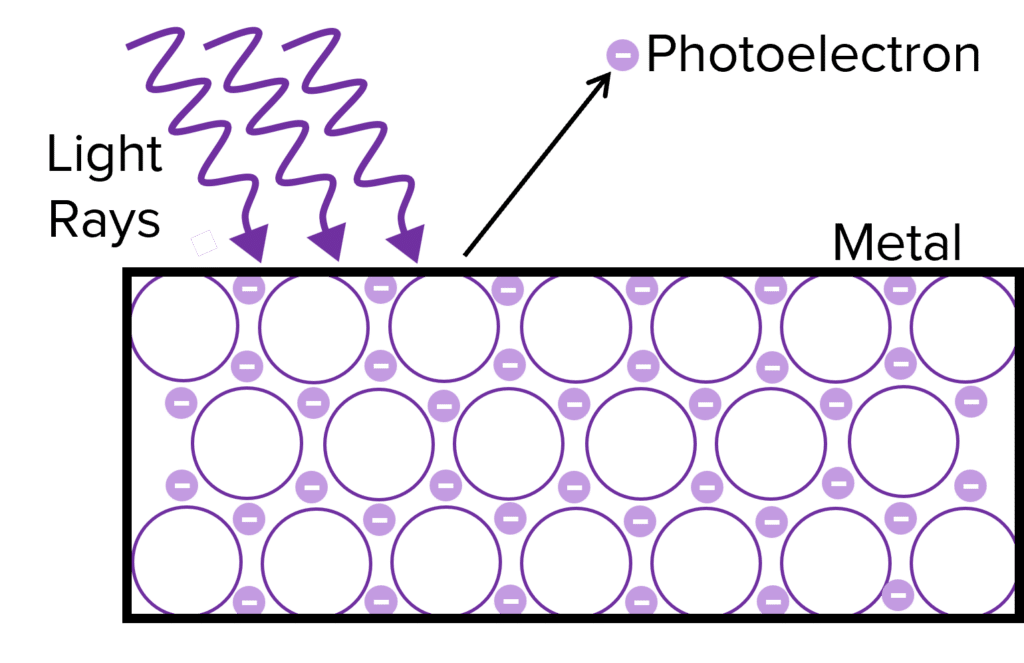

Photoelectrons are the particles emitted by the metal when the photoelectric effect occurs. They are electrons but are given a different name based upon their origin.
Threshold Frequency
The photoelectric effect does not happen in all metals, all the time. For the photoelectric effect to occur, the photons in the incident light ray must have sufficient energy such that it is enough to liberate surface electrons from the metal.
To calculate the energy of each photon we can use the equation:
E = hf
- E= the energy of a photon in joules \text{(J)}
- h= Planck’s constant (6.63\times 10^{-34} \text{ Js})
- f= the frequency of light in hertz \text{(Hz)}
Example Question:
Calculate the energy of a photon of light of frequency 450 \text{ THz}.
[2 marks]
\begin{aligned} \bold{E} &= \bold{hf} \\ E &= 6.63 \times 10^{-34} \times \textcolor{10a6f3}{450 \times 10^{12}}\\ &= \bold{2.98 \times 10^{19}} \textbf{ J} \end{aligned}
As we can see from the above equation, the energy of a photon and frequency are directly proportional.
Therefore, the minimum energy needed for the photoelectric effect to happen is directly proportional to a minimum frequency of light. This minimum frequency is known as the threshold frequency. The threshold frequency is different in each metal that we observe.
We also know from GCSE physics that v = f \lambda and as light is an electromagnetic wave which travels at the speed of the light (c). From this we get
c = f \lambda
which when rearranged for frequency gives:
f = \dfrac{c}{ \lambda}
Combining these equations gives us another equation we can use to calculate the energy of a photon:
\bold{E = \dfrac{hc}{ \lambda}}
Example Question:
A photon has of energy 4.2 \times 10^{-19} \text{ J} . What is its wavelength?
[2 marks]
E = \dfrac{hc}{ \lambda} \\ \begin{aligned} \bold{ \lambda} &= \bold{\dfrac{hc}{E}} \\ &= \dfrac{hc}{E} \\ &= \dfrac{6.63 \times 10^{-34} \times 3 \times 10^8}{\textcolor{f95d27}{4.2 \times 10^{-19}}} \\ &= \bold{4.74 \times 10^{-7}} \textbf{ m or } \bold{474} \textbf{ nm} \end{aligned}
As previously discussed, the threshold frequency of a metal is the minimum frequency of light needed to cause photoelectric emission. If a ray of light has a frequency lower than the threshold frequency, then it will not have enough energy to liberate an electron from the surface of the metal. However, if the light has frequency equal to the threshold frequency or greater, then photoelectric emission will occur.
Light as a Photon
As previously mentioned, the photoelectric effect provides evidence for the particle nature of light. As only a single electron in the metal can absorb a single photon of light, this brings the idea that photons must be tiny “packets” of quantised energy.
The Electronvolt
When using the equation listed previously for calculating the energy of a photon, our answer will be given in Joules \left(\text{J}\right).
However, cause each individual photon of light has such small amounts of energy, another unit called the electronvolt is used which is more suited for expressing very small amounts of energy.
\bold{1} \textbf{ electronvolt} is defined as the energy gained by an electron travelling through a potential difference of 1\text{ V} and is equal to 1.6 \times 10^{-19} \textbf{ J}.
To convert from \text{eV} to \text{J}, multiply by 1.6 \times 10^{-19} \text{ J}.
To convert from \text{J} to \text{eV}, divide by 1.6 \times 10^{-19} \text{ J}.
Work Function
Another key term often used when discussing the photoelectric effect is the work function (\Phi). The work function is defined as the minimum energy needed for a photoelectron to be released from the surface of the metal.
As the energy of a photon can be calculated using the equation, E = hf, we can see that the work function and threshold frequency are related. As threshold frequency is the minimum frequency needed for photoelectric emission to occur, we can say that:
\Phi = h \times f_{\text{threshold}}
- \Phi = the work function in joules \text{(J)}
- h= Planck’s constant (6.63\times 10^{-34} \text{ Js})
- f_{\text{threshold}}= the threshold frequency in hertz \text{(Hz)}
As only one photon can be absorbed by each electron, for the photoelectric effect to occur the photon must have equal to, or more energy than the work function of the metal. Any extra energy above the work function contributes to the kinetic energy of the photoelectron.
From this we can derive a new equation:
E_{\text{kmax}} = E_{\text{photon}} – \Phi
- E_{\text{kmax}} is the maximum kinetic energy of the photoelectron emitted by the photoelectric effect in joules \text{(J)}
- E_{\text{photon}}= the energy of the photon in joules \text{(J)}
- \Phi = the work function in joules \text{(J)}
Example Question:
The work function of a metal surface is 1.55 \text{ eV}. UV light of wavelength 430 \text{ nm} is incident on the metal.
Calculate the maximum kinetic energy of the photoelectrons.
[3 marks]
E_{\text{kmax}} = E_{\text{photon}} – \Phi
\\ \begin{aligned} E &= \dfrac{hc}{\lambda} \\ &= \dfrac{6.63 \times 10^{-34} \times 3 \times 10^8}{\textcolor{10a6f3}{430 \times 10^{-9}}} \\ &= 4.626 \times 10^{-19} \text{ J} \end{aligned}
\\ E_{\text{kmax}} = 4.626 \times 10^{-19} \text{ J} – (\textcolor{f21cc2}{1.55 \text{ eV}} \times 1.6 \times 10^{-19}) = \bold{2.15 \times 10^{-19}} \textbf{ J}
Stopping Potential
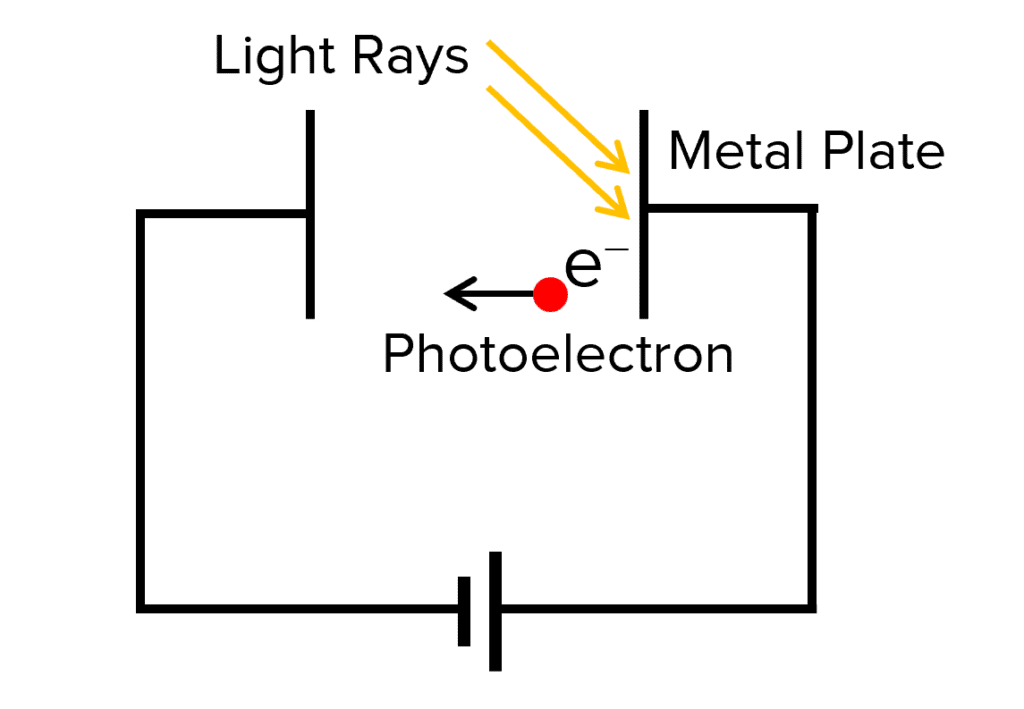

We can prevent the photoelectric effect happening in a piece of metal by applying a potential difference to the metal plate. This potential difference is known as the stopping potential Vs and is the potential difference required to stop the photoelectric effect from occurring.
As the voltage of the power source in the diagram above is increased, the metal plate becomes more positively charged and has a greater attraction holding the electrons in place, therefore increasing the amount of energy needed by the photon to cause photoelectric emission.
The Photoelectric Effect Example Questions
Question 1: Define the threshold frequency of a metal.
[2 marks]
Threshold frequency is the minimum frequency of electromagnetic waves incident on a metal needed to remove an electron from the surface.
Question 2: Sodium metal has a work function of 2.28 \text{ eV}. What is this in Joules?
[2 marks]
Question 3: The work function of a metal surface is 3.70 \text{ eV}. UV light of wavelength 233 \text{ nm} is incident on the metal.
Calculate the maximum kinetic energy of the photoelectrons in \text{eV}.
[4 marks]
In \text{eV}:
\dfrac{2.62 \times 10^{-19}}{1.6 \times 10^{-19}} = \bold{1.64} \textbf{ eV}You May Also Like...

MME Learning Portal
Online exams, practice questions and revision videos for every GCSE level 9-1 topic! No fees, no trial period, just totally free access to the UK’s best GCSE maths revision platform.