Forces and Exchange Particles
Forces and Exchange Particles Revision
Forces and Exchange Particles
For particles to interact with each other, there must always be one of the four fundamental forces involved. There also must be an exchange particle in the interaction. The importance of these will be discussed on this page.
Fundamental Forces
There are four fundamental forces in nature. These are the strong nuclear force, weak nuclear force, electromagnetic force and the gravitational force.
- Gravity is the weakest force and acts only on particles with mass. It has an infinite range.
- The weak nuclear force (also known as the weak interaction) affects all particles. It has the smallest range of any of the forces, acting over a distance of up to 10^{-18} \: \text{m}.
- The electromagnetic force acts only on charged particles and occurs over an infinite range.
- The strong nuclear force (also known as the strong interaction) affects only hadrons. It is the strongest force but only acts over a distance of 10^{-15} \: \text{m}.
Exchange Particles
When two particles interact with each other, an exchange particle passes between them. This is required because it is impossible for there to be an instantaneous action over a distance. The exchange particle acts as a force carrier between the particles.
The exchange particle is also known as a virtual particle. It only exists for a very brief moment and its only role is to carry the force between the particles. It is not observed and is hence called virtual.
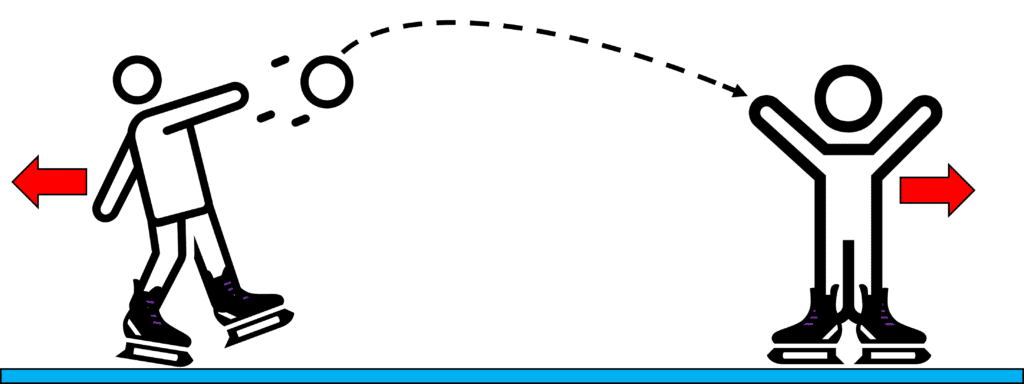
To visualise the interaction for a repulsion, imagine two people throwing a ball (or snowball!) while on ice.
When one person throws the ball, they will move backwards to conserve momentum.
When the other person catches the ball, they will also move backwards, again to conserve momentum.
In this exchange, both people have moved further away from one another. This interaction between the people continues therefore they ‘repel’ each other. The ball is our exchange particle here.
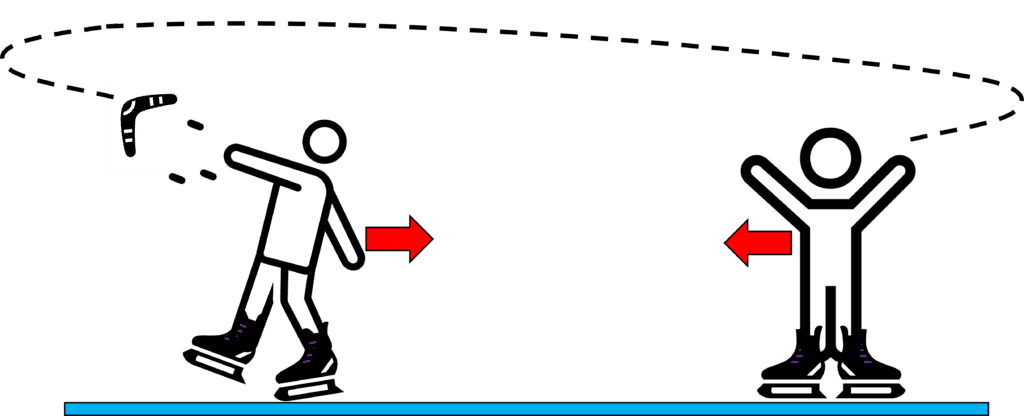
For attraction, this time we replace the ball with a boomerang and have the people facing in the opposite direction.
When one person throws the boomerang, they will move backwards, towards the other person.
When the other person catches the boomerang, they will also move backwards towards the original thrower. This occurs due to conservation of momentum. This interaction between the people continues therefore they ‘attract’ each other.
Each of the fundamental interactions has their own exchange particle, also known as gauge bosons. You need to know 3 of the gauge bosons: virtual photons, the \textcolor{f21cc2}{W} bosons and pions.
The virtual photon is the gauge boson for the electromagnetic interaction. It has zero mass, which gives the electromagnetic force an infinite range.
Pions are the gauge boson for the strong interaction between nucleons. The mass of a gauge boson affects the range of the force, hence the strong force does not have an infinite range. As pions are relatively heavy, they have a small range. The strong nuclear force is also involved in quarks, which use gluons \left(g\right) instead as the gauge boson.
The \textcolor{f21cc2}{W} bosons (W^{+} and W^-) are the gauge bosons for the weak interaction. The \textcolor{f21cc2}{W} bosons weigh around 100 times greater than a proton and are the heaviest gauge boson. This gives the \textcolor{f21cc2}{W} bosons a very small range as a large amount of energy is needed to create the exchange particle. It therefore only exists for a brief time and travels a short distance.
Gravity is very weak, therefore is not considered in particle interactions. It has a theoretical gauge boson called the graviton, however this has not yet been discovered.
| Interaction | Affected Particles | Gauge Boson | Range of Interaction |
| Strong | Hadrons |
Pions (Particles) |
10^{-15} \: \text{m} |
| Electromagnetism | Charged particles | Virtual Photon | Infinite |
| Weak | All particles | W Bosons \left(W^- \text{,} \: W^+\right) | 10^{-18} \: \text{m} |
| Gravity | Particles with mass | Graviton (Theoretical, not observed or confirmed) | Infinite |
Feynman Diagrams
Particle interactions are physically represented through Feynman diagrams. They show the incoming and outgoing particles as well as the exchange particle.
There is a clear set of rules that must be followed:
- The vertical axis represents time. All incoming particles must start from the bottom.
- The horizontal axis represents space.
- Particles are represented using straight lines. Gauge bosons are represented using wiggly lines. All lines must not cross.
- All straight lines must have an arrow indicating their forward direction through time. Neutral gauge bosons do not need to have an arrow, charged gauge bosons must have an arrow.
- Baryon and lepton number and total charge must be conserved on each side of the gauge boson.
Feynman diagrams are not an actual spatial representation of the interaction, hence line distances and angles are of no value.
You may find that anti-particles are shown to travel backwards through time. This is to be ignored at A Level.
You should memorise some of the following common Feynman diagrams:
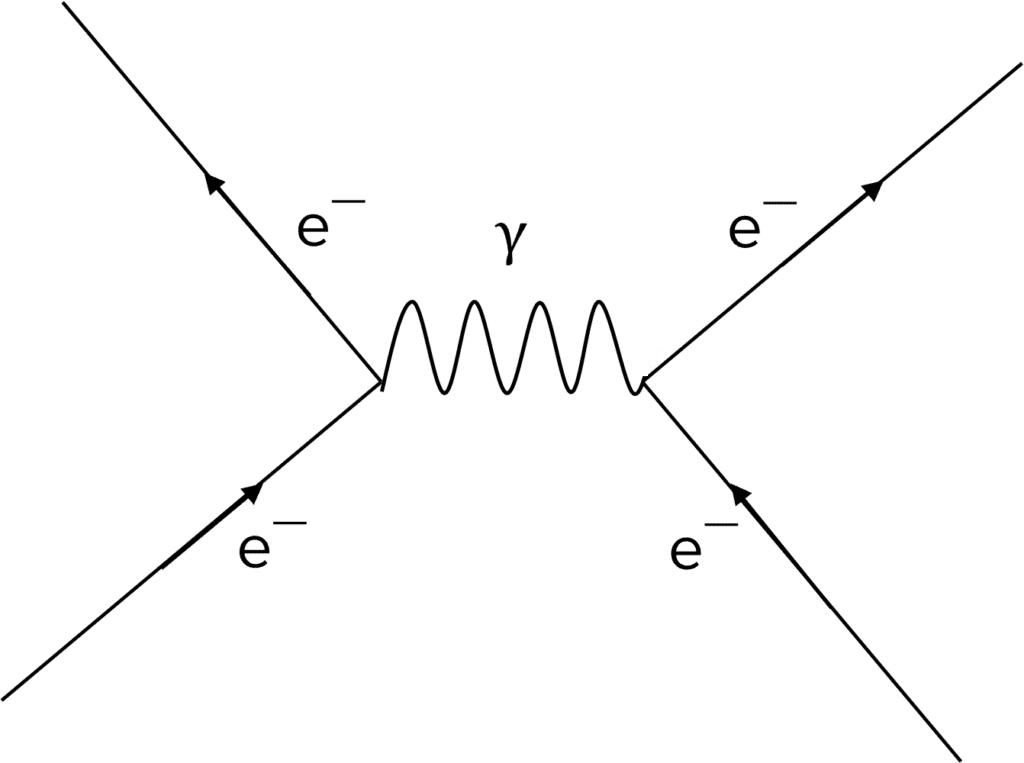
Electromagnetic Repulsion
When two particles of the same charge are placed near each other, they are electromagnetically repelled from each other. They exchange a virtual photon between each other.
The same diagram is used for both electron, positron and proton repulsion. Note that as the photon has no charge, the wiggly line representing the gauge boson does not have an arrow.
Electron Capture and Electron-Proton Collisions
Electrons and protons are oppositely charged and therefore attract each other through the electromagnetic force. However, they can also interact with each other through the weak interaction through electron capture and electron proton collisions. Both have the same decay equation:
p + e^- \: \rightarrow \: n + v_e
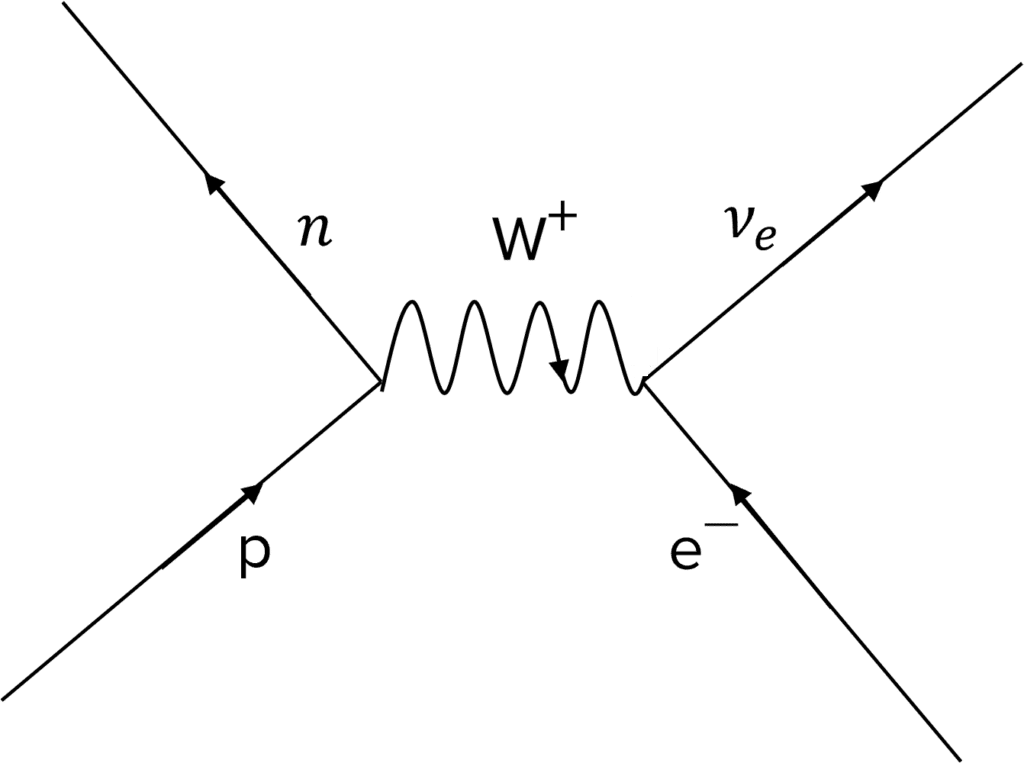
Electron capture is when an electron is absorbed by a proton in the nucleus. This results in the proton decaying to a neutron and an electron neutrino being released. This interaction is mediated by the \textcolor{00bfa8}{W^+} boson.
Note that the baryon number is conserved on the left side of the diagram and the lepton number is conserved on the right side of the diagram.
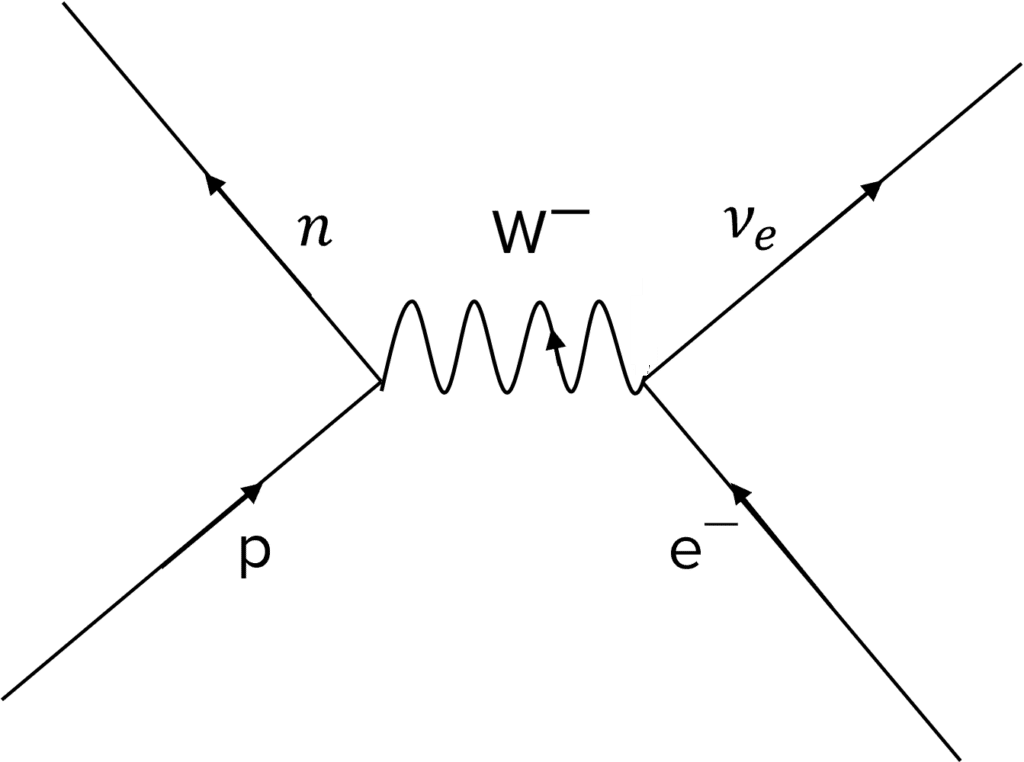
Electron-proton collisions occur when an electron collides with a proton, with the same particles released, a neutron and electron neutrino. However, this interaction is mediated by the \textcolor{00bfa8}{W^-} boson, hence the arrow is in the opposite direction.
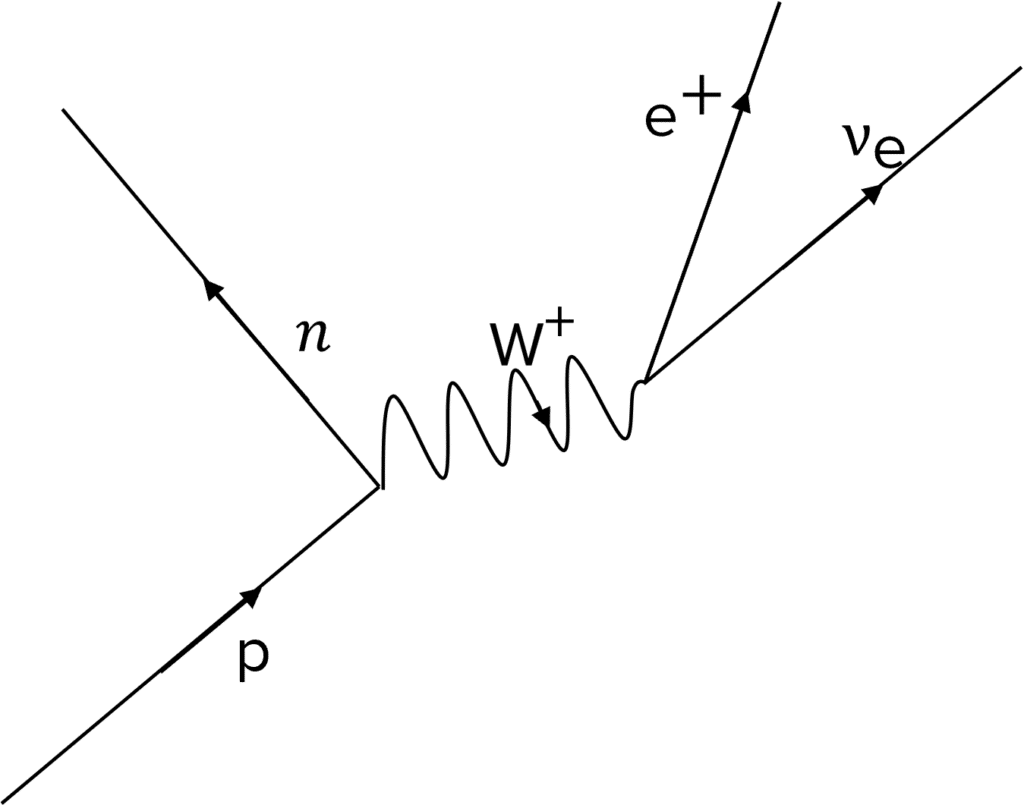
Beta-plus and Beta-minus decay
Beta-plus decay involves a proton turning into a neutron, with a positron and electron neutrino being released. The gauge boson in this interaction is the \textcolor{00bfa8}{W^+} boson.
The decay equation for this interaction is
p \: \rightarrow \: n + e^+ + v_e
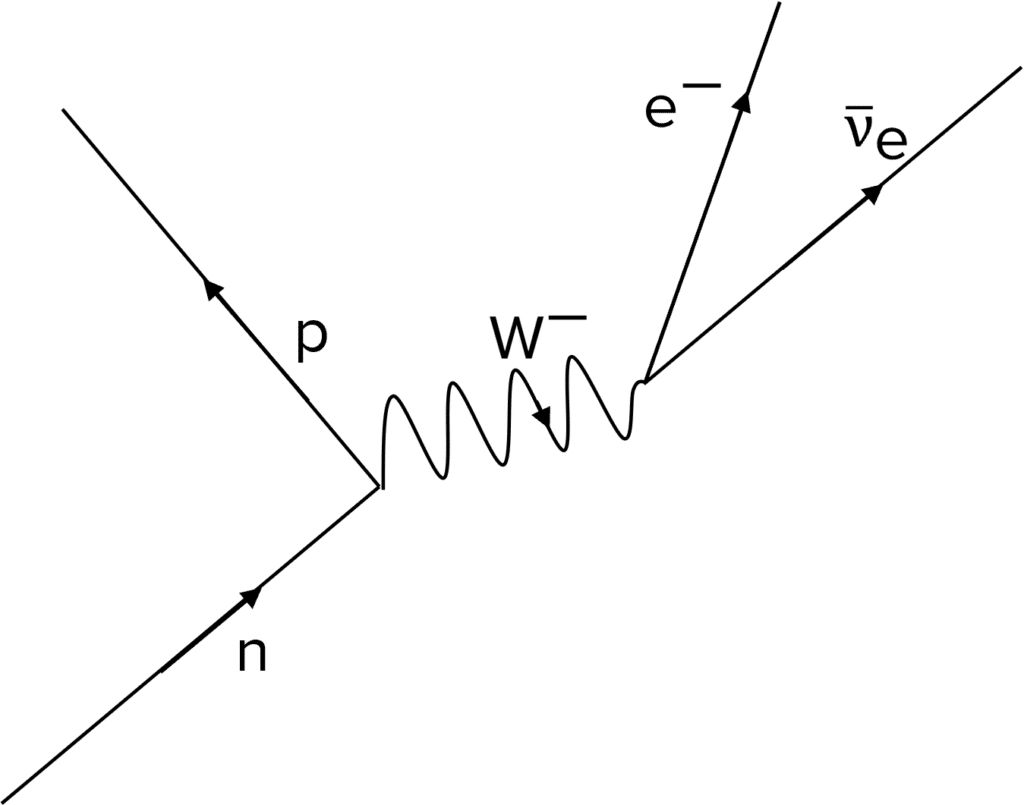
Beta-minus decay involves a neutron turning into a proton, with an electron and electron antineutrino being released. The gauge boson in this interaction is the \textcolor{00bfa8}{W^-} boson.
The decay equation for this interaction is:
n \: \rightarrow \: p + e^- + \bar{v}_e
Conservation Laws in Particle Interactions
There are a set of conservation laws that particle interactions must obey. The following properties must be conserved in all particle interactions:
- Charge \left(Q\right)
- Baryon and Lepton Number \left(B \text{,} \: L\right)
- Energy \left(E\right)
- Momentum \left(\rho\right)
Strangeness must be conserved in the strong interaction but does not have to be conserved in the weak interaction.
To determine whether an interaction is possible, calculate the quantum number on each side of the equation and check whether they are equal (unless it is strangeness in a weak interaction).
Example: Using the Conservation Laws
Identity the unknown particle in the following particle interaction using the conservation laws.
p^+ \: \rightarrow \: n + \pi^+ + X
[3 marks]
All particle interactions need to follow the conservation laws. Therefore, by checking each one, we can determine the makeup of the unknown particle.
Charge:
\begin{aligned} p^+ \: &\rightarrow \: n + \pi^+ + X \\ +1 \: &\rightarrow \: 0 + +1 + X \end{aligned}LHS = +1, RHS = +1 + X. As LHS = RHS, X must equal 0. Therefore we know that the unknown particle has a charge of 0 and is neutral.
Baryon Number:
\begin{aligned} p^+ \: &\rightarrow \: n + \pi^+ + X \\ +1 \: &\rightarrow \: +1 + 0 + X \end{aligned}LHS = +1, RHS = +1 + X. As LHS = RHS, X must equal 0. Therefore we know that the unknown particle has a baryon number of 0 and cannot be a baryon. It must be a lepton or meson.
Lepton Number:
\begin{aligned} p^+ \: &\rightarrow \: n + \pi^+ + X \\ 0 \: &\rightarrow \: 0 + 0 + X \end{aligned}LHS = 0, RHS = 0 + X. As LHS = RHS, X must equal 0. Therefore we know that the unknown particle cannot be a lepton. It must be a meson.
Strangeness:
\begin{aligned} p^+ \: &\rightarrow \: n + \pi^+ + X \\ 0 \: &\rightarrow \: 0 + 0 + X \end{aligned}There are no strange quarks on the LHS of the equation. Therefore, strangeness must be conserved if any strange quarks are created. On the right hand, the 2 known particles do not have any strange quarks, therefore it is not possible for particle X to have a strange quark (as this would violate the strangeness conservation rule). Therefore X is not a kaon.
So particle X must have a charge of 0, a baryon number of 0, a lepton number 0 and it does not have a strange quark. Hence X is a neutral pion \left(\pi^0\right).
Research in Particle Physics
Particle physics is an ever-changing field, with multiple ongoing experiments that are looking to provide evidence for theories that confirm our understanding of the universe.
Scientists use the results of existing experiments to hypothesise a new theory, for example a new particle or a property of a particle. One example already seen is the existence of the neutrino for the conservation of energy in beta decay.
Experiments are performed to test this theory and the results may be combined with the results from other experiments to confirm the theory. If the combined results of the experiments confirm the theory, then the theory is validated.
Usually, experiments are repeated numerous times to reduce experimental uncertainty and increase the confidence that the theory is valid.
In science, a theory is only valid if experiments continue to validate the theory. The theories we have now are our current best understanding of the universe, further experiments may validate different theories, which may replace our current understanding. Therefore, the field of particle physics is a continually changing field.
To test particle physics theories, quite often a significant amount of energy is required. Particles are often required to travel at very high speeds (close to the speed of light) before colliding. To achieve this, scientists use particle accelerators.
Particle accelerators are designed to give particles enough energy to reach very high speeds. They often use superconducting magnets to accelerate and maintain a high speed for the particles.
The largest particle accelerator in the world is the Large Hadron Collider (LHC) at CERN in Geneva. It is 17 miles long (crossing the borders of France and Switzerland) and cost \text{£}2.6 \text{ billion} at the time to build. Scientists across the world work at CERN, with over 17500 scientists contributing to their research. The LHC is the site of one of the biggest breakthroughs in modern particle physics, the observation of the Higgs Boson.
Forces and Exchange Particles Example Questions
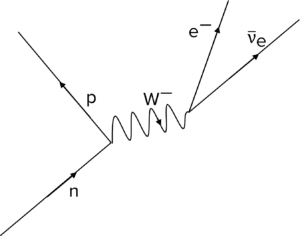
Question 1: Draw a diagram that shows a beta-minus decay, ensuring to label all particles involved.
[3 marks]
Question 2: Given the following decay, which property is not conserved?
n \: \rightarrow \: \bar{p} + e^+ + \bar{v}_e
[1 mark]
n \: \rightarrow \: \bar{p} + e^+ + \bar{v}_e
\begin{aligned} \text{Charge:}& \: 0 \: \rightarrow \: -1 +1 +0 \\ \text{Baryon Number:}& \: +1 \: \rightarrow -1 + 0 + 0 \\ \text{Lepton Number:}& \: 0 \: \rightarrow \: 0 + 1 - 1 \end{aligned}No strange quarks, therefore strangeness is conserved. Baryon number is not conserved.
Question 3: A \Lambda^0 particle has a quark combination of uds. It can decay into a proton and a second particle X, determine X and state the interaction.
[3 marks]
\Lambda^0 \: \rightarrow \: p + X
\text{Charge:} \: 0 \: \rightarrow +1 + X
Therefore, X must be a negatively charged particle \left(-1\right).
\text{Baryon Number:} \: +1 \: \rightarrow +1 + XTherefore, X cannot be a baryon. It has to be either a meson or lepton.
\text{Lepton Number:} \: 0 \: \rightarrow 0 + XTherefore, X cannot be a lepton. It has to be a meson.
\text{Strangeness:} \: -1 \: \rightarrow 0 + X .
X cannot be a Kaon, as it has no strange quarks. Remember strange particles are produced in pairs and we know a proton does not contain any strange quarks.
Therefore \boldsymbol{X} is a negative pion \boldsymbol{\left(\pi^-\right)}.
The particle interaction must be the weak interaction as strangeness is not conserved.
Forces and Exchange Particles Worksheet and Example Questions
Particle Physics Questions
A LevelOfficial MMEYou May Also Like...
MME Learning Portal
Online exams, practice questions and revision videos for every GCSE level 9-1 topic! No fees, no trial period, just totally free access to the UK’s best GCSE maths revision platform.
