Series and Parallel Circuits

Kirchhoff’s first law states that “the sum of all currents entering a junction is always equal to the current leaving a junction”. This shows the ideas of conservation of energy and conservation of charge.

Example: In the circuit below, A_1 measures a current of 10 \text{ A}. Assuming both branches of the circuit are identical, what would the other ammeter readings show?

[5 marks]

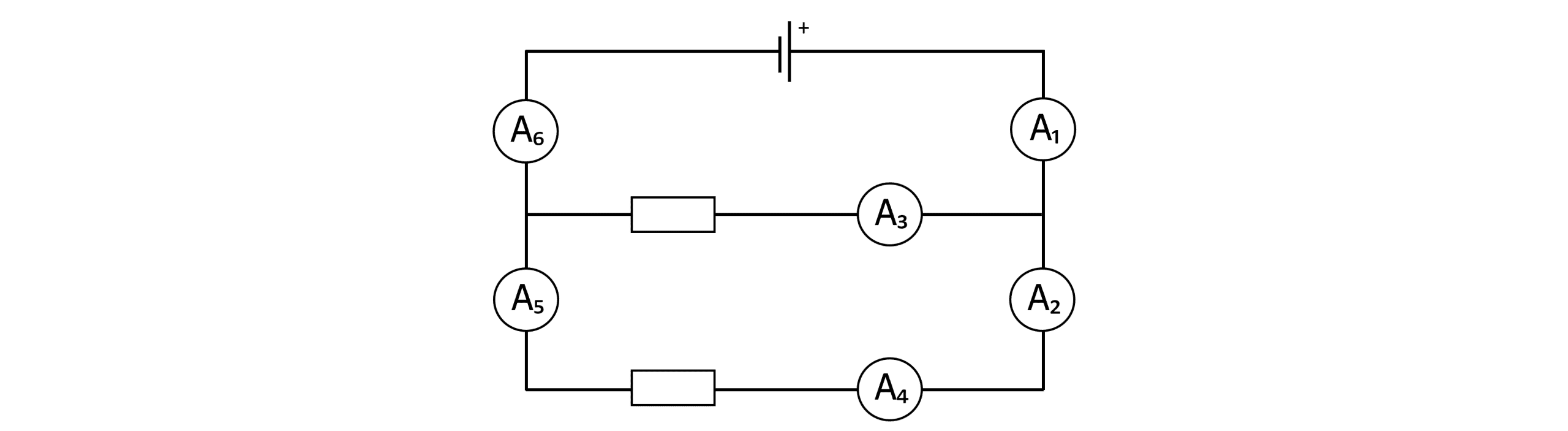
Applying Kirchoff’s first law:

\begin{aligned} \bold{A_1} &= \bold{10} \textbf{ A} \\ \bold{A_2} &= \bold{5} \textbf{  A} \\ \bold{A_3} &= \bold{5} \textbf{ A} \\ \bold{A_4} &= \bold{5} \textbf{ A} \\ \bold{A_5} &= \bold{5} \textbf{ A} \\ \bold{A_6} &= \bold{10} \textbf{ A} \end{aligned}

Kirchhoff’s second law states that the total emf in a circuit is equal to the sum of the potential differences across each component.

Example: Calculate the reading on both voltmeters assuming that the resistors are identical.

[2 marks]

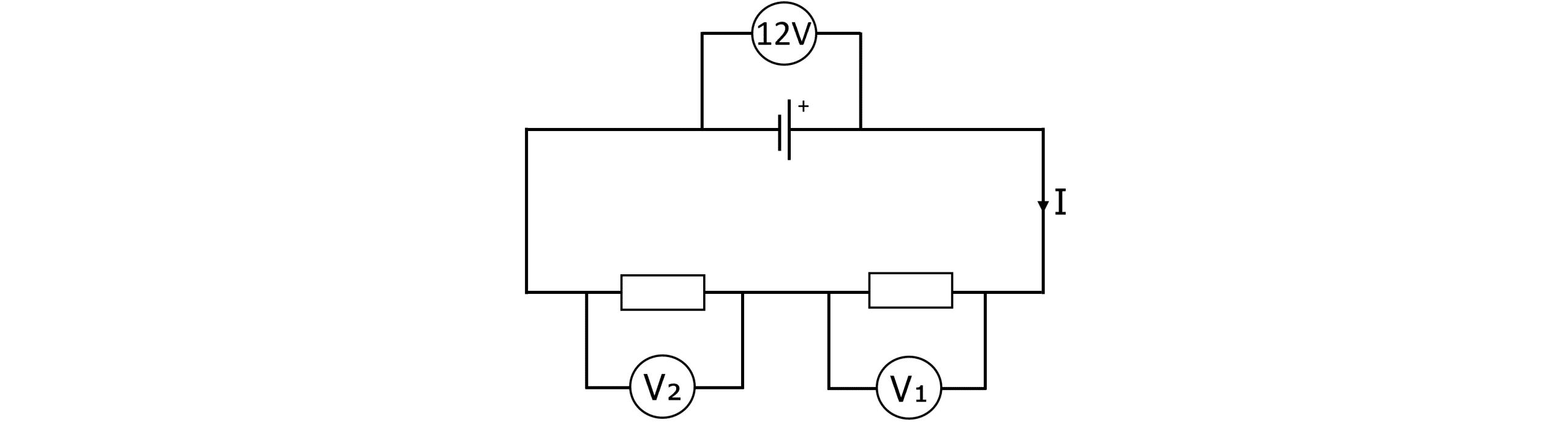
Kirchoff’s seconds law: 

\bold{V_1 + V_2 = 12}\textbf{ V} \\ V_1=V_2= \bold{6}\textbf{ V}

It is important to understand the characteristics of series and parallel circuits. These characteristics can then be used to form a basis for our calculations.

Series circuits

In a series circuit, the current is the same at all points of the circuit and therefore, all components have the same current.

I_t= I_1 = I_2=I_3 ....  

However, potential difference is shared among the components of a series circuit. 

V_t=V_1+V_2+V_3

If more than one cell is connected in series, the total voltage produced is equal to the sum of all the cells.

 

Parallel circuits 

In a parallel circuit, the current is shared among the branches of the circuit. Therefore:

I_t=I_1+I_2+I_3 ...

However, potential difference is equal in all branches of a parallel circuit. 

V_t=V_1=V_2=V_3

If cells are connected in parallel, the total terminal pd is the same as one of the cells. 

The total resistance in a circuit is calculated differently depending upon if the circuit is series or parallel. 

Resistors in a series circuit are added together to find the total resistance. This can be summarised in the equation:

R_t=R_1+R_2+R_3...

Example: what is the total resistance in this circuit?

[1 mark]

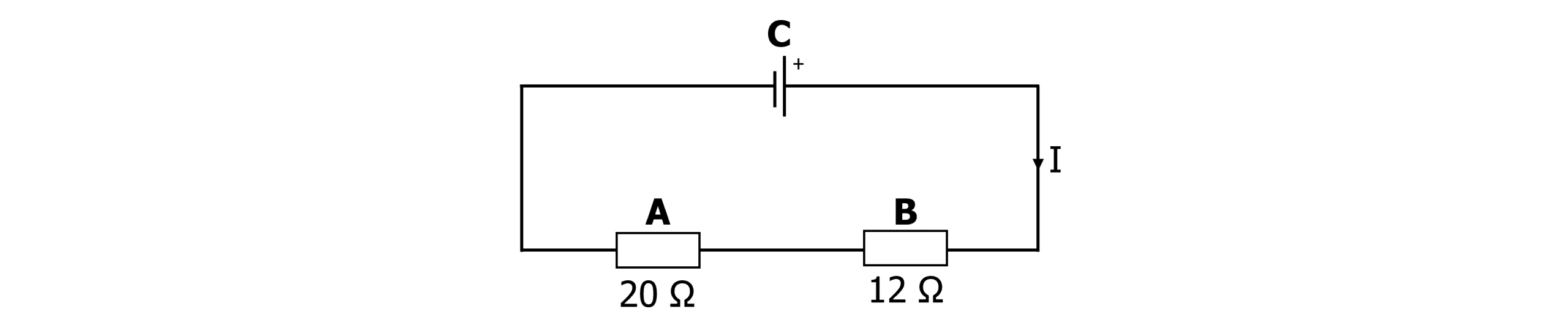
\begin{aligned} R_t &= R_1 + R_2 + R_3... \\ &= 20+12 \\ &= \bold{32 \, \Omega} \end{aligned}

Resistors in parallel are more difficult to combine. The total resistance when resistors are added in parallel can be calculated using the equation:

\dfrac{1}{R_t} = \dfrac{1}{R_1}+\dfrac{1}{R_2}+\dfrac{1}{R_3}...

Example: what is the total resistance in this circuit?

[3 marks]

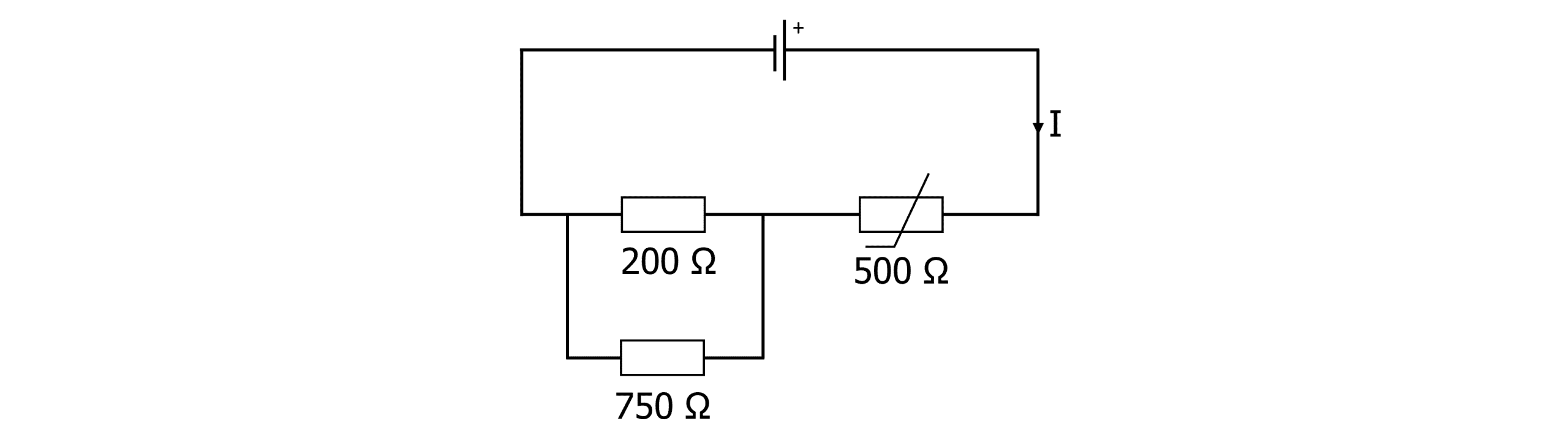
This example is made of resistors in series with one in parallel. Firstly, we must add the two resistors in parallel.

\begin{aligned}\dfrac{1}{R_t} &= \dfrac{1}{R_1}+\dfrac{1}{R_2}+\dfrac{1}{R_3}... \\ &= \bold{\dfrac{1}{200}+\dfrac{1}{750}} \\ &= 6.33 \times 10^{-3} \\ R_t &= \dfrac{1}{6.33 \times 10^{-3}} \\ &= \bold{158 \, \Omega} \end{aligned}

Now add the other resistor in series:

\begin{aligned} R_t&=R_1+R_2+... \\ &= 158 + 500 \\ &= \bold{658 \Omega} \end{aligned}

Using this equation, the total resistance of resistors combined in parallel is less than the resistance of the smallest resistor. Therefore, combining resistors in parallel can be used to reduce the resistance in a circuit.

Power is defined as “the rate of doing work” or how much energy is used by a circuit component per unit of time. It is measured in Watts \text{(W)} or \text{(Js}^{-1}\text{)} as an alternative unit. 

There are several different ways of calculating electrical power, depending on what information you have been given:

P=\dfrac{E}{t}

• P= power in watts \text{(W)}
• E= energy in joules \text{(J)}
• t= time in seconds \text{(s)}

P=VI

• P= power in watts \text{(W)}
• V= potential difference in volts \text{(V)}
• I= current in amps \text{(A)}

P=\dfrac{V^2}{R}

• P= power in watts \text{(W)}
• V= potential difference in volts \text{(V)}
• R= resistance in ohms (\Omega)

P=I^2R

• P= power in watts \text{(W)}
• I= current in amps \text{(A)}
• R= resistance in ohms (\Omega)