Resistance and Resistivity
Resistance and Resistivity Revision
Resistance and Resistivity
Previously we have learnt that resistance is an opposing force against current. It’s resistance that opposes the flow of charge carriers around the circuit. In this section we look at the factors that affect resistance and the idea of resistivity. We will also discuss thermistors and superconductors.
Resistance
Resistance occurs because charge carriers do not have a free path through wires or components. As the free electrons pass through a wire, they collide with the ions that make up the metal wire, slowing them down and consequently, reducing the current.
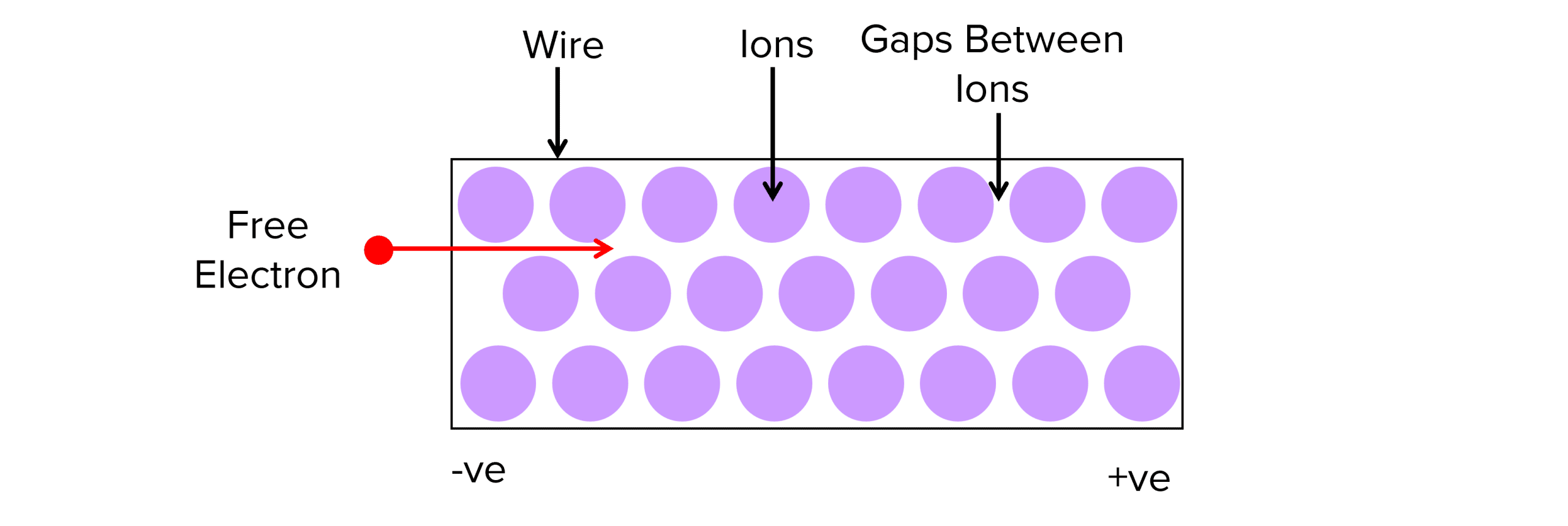
Changing the properties of the wire changes the resistance. The resistance of a piece of wire is affected by several factors :
- Length – as length increases, so does the resistance. There is a directly proportional relationship between length and resistance. Because the wire is longer, there are more ions for the free electrons to pass through and therefore, an increased chance of a collision.
- Cross-sectional area – there is an inversely proportional relationship between cross-sectional area and resistance. As cross-sectional area increases, resistance decreases. This is because as the cross-sectional area increases, there are more routes for the free electrons to pass through, and therefore, less chance of collisions happening.
- Temperature – there is a directly proportional relationship between temperature and resistance. As temperature increases, so does resistance. When the ions gain thermal energy, they begin to vibrate more. As the free electrons try to pass through the vibrating ions, they are more likely to collide the more the ions are vibrating.
- Material – finally, the material affects resistance. Some metals are better at conducting than others. This may be due to the ions being less densely packed, or the metal containing more free electrons to carry the charge.
Resistivity
The above factors contribute to the resistivity of a wire. The resistivity of a wire tells us how good it is at conducting electricity. The lower the resistivity, the better the electrical conductor. It is a more effective way of comparing materials than resistance as it takes into account the differences in length and cross sectional areas of the wires. However, as the equation does not take into account temperature, this would still need to be controlled to effectively compare wires.
To calculate resistivity, the following equation is used:
R=\dfrac{\rho L}{A}
- R= resistance in ohms (\Omega)
- \rho= resistivity in ohm metres (\Omega \text{m})
- L= the length of the wire in metres \text{(m)}
- A= the cross sectional area of the wire in square metres \text{(m}^2\text{)}
Example:
A wire of length 2 \text{ m}, cross sectional area 0.05 \text{ m}^2 and resistance 20 \Omega. What is the Resistivity of the wire?
[2 marks]
\bold{R=\dfrac{\rho L}{A}}
Rearrange for resistivity:
\begin{aligned} \rho &= \dfrac{RA}{L} \\ &= \dfrac{\textcolor{aa57ff}{20} \times \textcolor{10a6f3}{0.05}}{\textcolor{00d865}{2}} \\ \bold{0.5 \, \Omega}\textbf{m} \end{aligned}
Thermistors
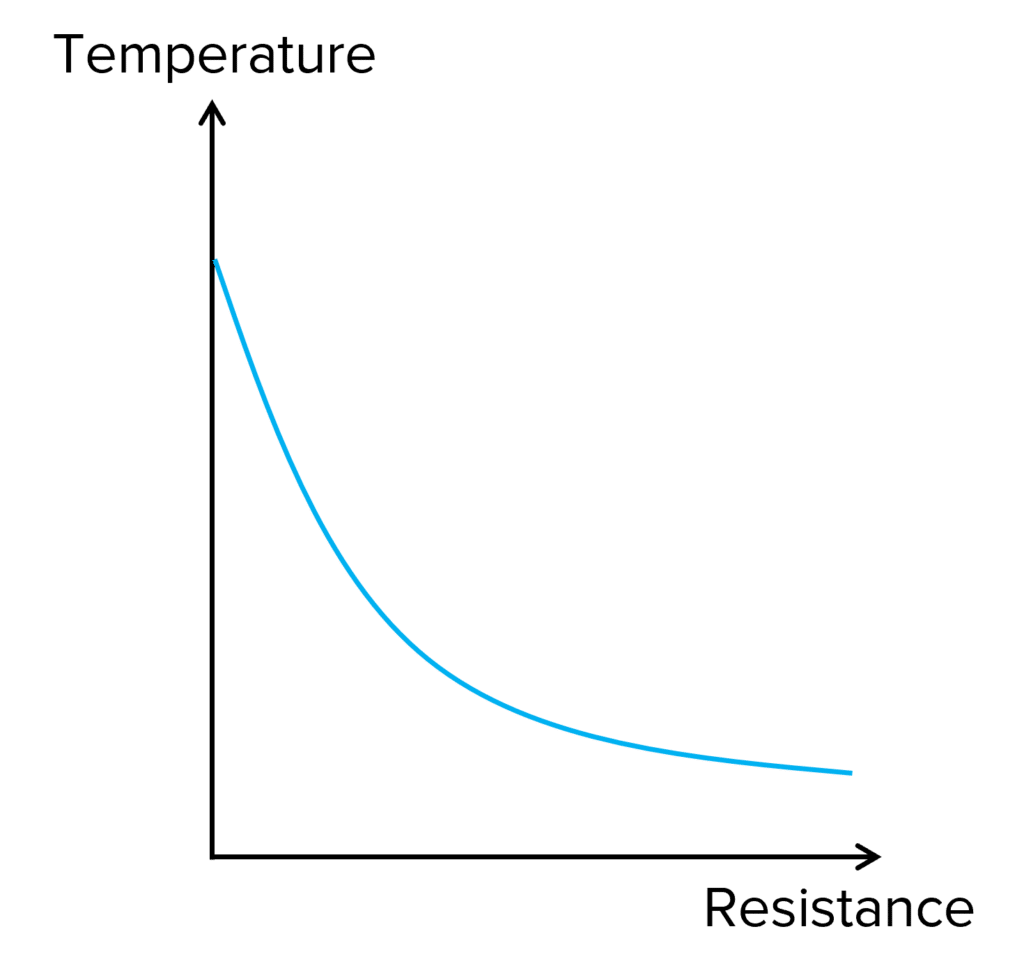

A thermistor is a component whose resistance is variable and is dependent on temperature. They are very useful as they can be used in many heating appliances as a thermostat. Unlike most components, a thermistor is designed to lower in resistance as temperature increases.
As the thermistor increases in temperature, it releases more charge carriers into the circuit, increasing the current and consequently, decreasing the resistance.
Superconductors
A superconductor is a material that has no resistance when below its critical temperature. However, it can only reach superconductivity given the correct conditions and the material has the capability of being a superconductor.
All superconductors require very low temperatures. The temperature at which superconductivity is reached is known as the critical temperature. For most materials the critical temperature is below 10 \text{ K or } -273 \degree \text{C}.
Superconductors have several applications and sat usually used when very high currents are required. Some of the applications include:
- Situations where a strong magnetic field is required such as MRI scanners, Maglev trains, Particle accelerators.
- To reduce energy loss to the surroundings.
Required Practical 5
Determining the resistivity of a wire.
Doing the experiment:
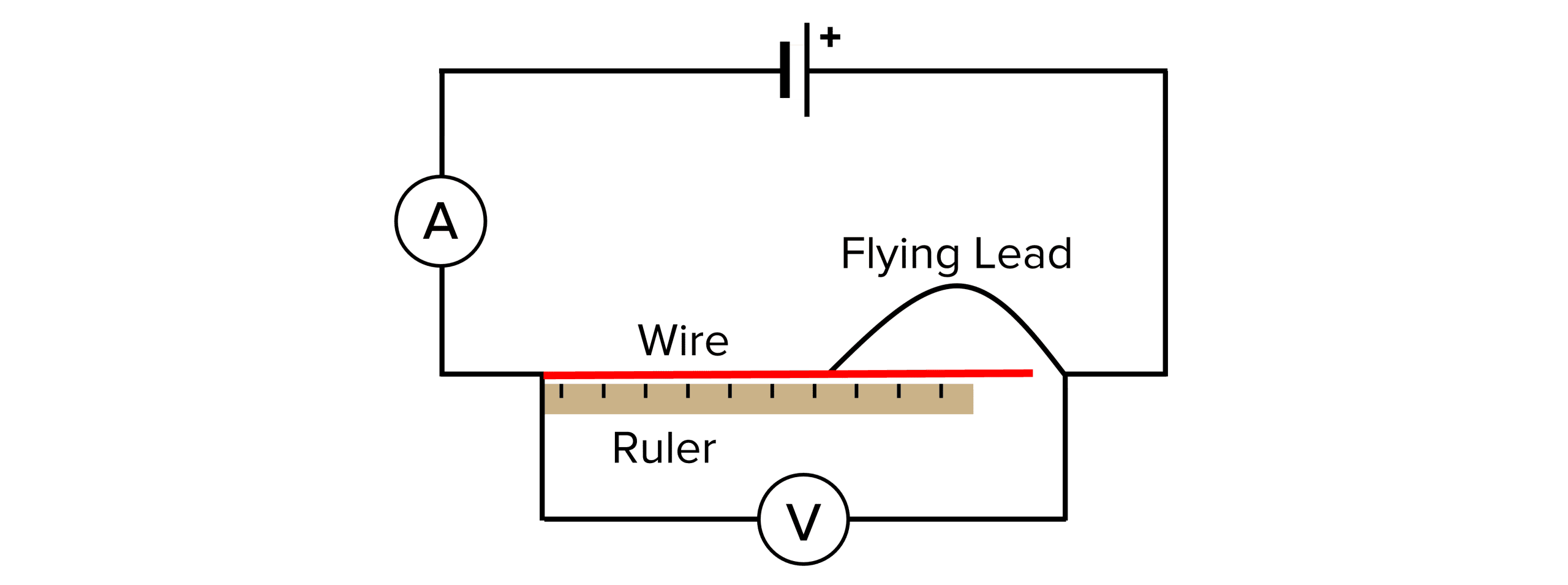
- Set up the experiment as shown in the diagram.
- Firstly, the diameter of the wire needs to be measured. A micrometer can be used for this. Measure the diameter of the wire in three different places and orientations along the wire before taking an average. Be careful not to squash the wire by over tightening the micrometer.
- Ensure the wire is secured at the zero end of the ruler before starting using a g-clamp.
- Begin by setting the power supply to 6 \text{ V} and connecting the flying lead to the wire at 0.20 \text{ m}. Switch the power supply on and take the readings for current and voltage then immediately switch off again. This should avoid heating the wire and causing an increase in resistance.
- Repeat this procedure for varying lengths of wire and repeat each length 3 times before calculating an average for current and voltage.
Analysing the results:
Firstly, resistance needs to be calculated using the equation:
R=\dfrac{V}{I}
This should be done for each pair of values.
Using the value for resistance, the resistivity can be calculated using he equation:
R= \dfrac{\rho L}{A}.
Alternatively, a graph can be plotted of resistance on the y-axis and length on the x-axis. The gradient of this graph would represent \dfrac{\rho}{A}. Therefore, the restivity is calculated by multiplying the gradient of the graph by the cross-sectional area.
The experiment can be completed for different materials of wire to make comparisons of resistivity.
Resistance and Resistivity Example Questions
Question 1: Describe the benefit of using resistivity to compare two materials instead of resistance.
[2 marks]
Resistivity is a better comparative measure as it takes into account the length and cross-sectional area whereas resistance doesn’t. Resistance could only be used to compare materials if they had the same length and cross sectional area.
Question 2: Explain why an increase in temperature causes a thermistor to reduce in resistance.
[3 marks]
As the temperature increases, the thermistor releases more charge carriers into the circuit. As the number of charge carriers increases, the resistance decreases and the current increases.
Question 3: Describe what a superconductor is and explain how a superconductor would improve the efficiency of a particle accelerator.
[3 marks]
A superconductor is a material with no resistance below its critical temperature. A superconductor would improve the efficiency by reducing the amount of energy dissipated to the surroundings. Therefore, less energy would be needed as the accelerator would be more efficient.








