Radioactive Decay
Radioactive Decay Revision
Radioactive Decay
We have looked at the properties of alpha, beta and gamma decay. Each of these may be emitted as part of radioactive decay.
What is Radioactive Decay?
Radioactive decay is the random and spontaneous decay of the nucleus of an atom to become more stable, resulting in the emission of alpha, beta or gamma radiation.
When looking closely at a radioactive source, it is impossible to predict which nucleus will decay and when it will decay. This is because the process is completely random. It is also important to remember that no changes in the conditions surrounding a source will affect its rate of decay.
Activity
The activity (A) of a radioactive source is the average number of nuclei that decay per unit of time. Notice two things from this definition:
- Average – as radioactive decay is random, the number of nuclei that decay per unit of time varies. We can however state the average number of decaying nuclei per unit of time.
- The definition states per unit of time. This unit of time can vary depending upon which isotope is being observed and how quickly they decay.
A radioactive source that is described as highly radioactive has a high activity. This is measured in Becquerels \text{(Bq)} where \bold{1} \text{ Bq}= \bold{1} decaying nuclei per second.
The equation used to calculate activity is as follows:
A=\dfrac{\Delta N}{\Delta t}
- A= the activity in becquerels \text{(Bq)}
- \Delta N= the number of decayed nuclei
- \Delta t= the change in time in seconds \text{(s)}
Example: Over a period of one hour, a GM counter detects 25,000 counts of radiation. What is the activity of the source? The background radiation has been measured at 1 count per second.
[3 marks]
Substitute the given values into the activity equation:
\begin{aligned} \bold{A} &= \bold{\dfrac{\Delta N}{\Delta t}} \\ &= \dfrac{\textcolor{f43364}{25, 000}}{\textcolor{10a6f3}{60 \times 60}} \\ &= \bold{6.9} \text{ Bq} \end{aligned}
Subtract the background radiation:
6.9 - \textcolor{00d865}{1} = \bold{5.9} \textbf{ Bq}
We can also use the decay constant (\lambda) to describe how radioactive a source is. The decay constant is the probability that a nuclei will decay per second. Decay constant is related to activity using the following equation:
A= \lambda N
- A= the activity in becquerels \text{(Bq)}
- \lambda = the decay constant per second \text{(s}^{-1}\text{)}
- N= the number of nuclei in a sample
Example: A source contains 6 \times 10^{24} undecayed nuclei. If the decay constant is 2.1 \times 10^{-6} \text{ s}^{-1}, calculate the activity of the source.
[2 marks]
Substitute the values into the equation linking activity and decay constant:
\begin{aligned} \bold{A} &= \bold{\lambda N} \\ &= \textcolor{f95d27}{2.1 \times 10^{-6}} \times \textcolor{ffad05}{6 \times 10^{24}} \\ &= \bold{1.3 \times 10^{19}} \textbf{ Bq} \end{aligned}
Exponential Decay
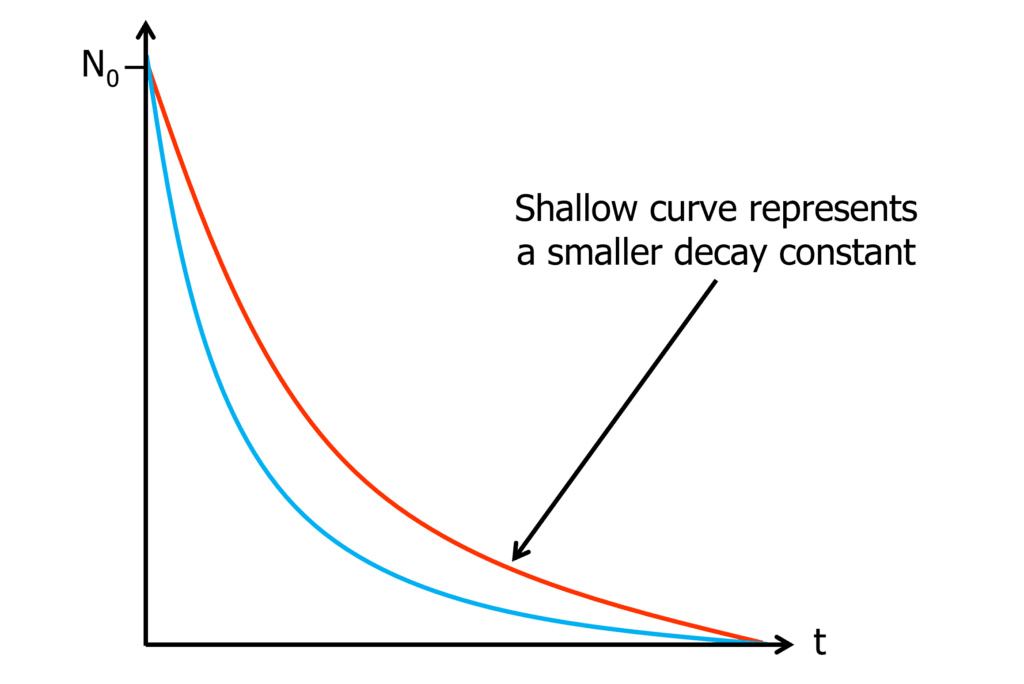

It’s common to see radioactive decay graphs like the one below. This graph shows how the number of undecayed nuclei \text{(N)} varies with time \text{(t)}.
This type of decay curve is an exponential decay curve. The number of nuclei begins to decay from N0 (initial number of nuclei) rapidly but the rate of decay slows over time until almost reaching zero.
The steeper slope, represented above in black, shows a decay with a higher decay constant compared to the shallower red line.
Radioactive Decay Equations
Because of the nature of exponential decay, it can be difficult to predict how many nuclei would be remaining in a sample after a certain amount of time. A calculation can be completed to calculate this number:
N=N_0e^{-\lambda t}
- N= the number of undecayed nuclei
- N_0= the initial number of undecayed nuclei
- \lambda = the decay constant per second \text{(s}^{-1}\text{)}
- t= the time in seconds \text{(s)}
As the activity of a source and the count rate also decays exponentially, the equation may also be written as:
A=A_0 e^{- \lambda t}
- A= the activity at a given time (t) in becquerels \text{(Bq)}
- A_0 the initial activity in becquerels \text{(Bq)}
- \lambda= the decay constant per second \text{(s}^{-1}\text{)}
- t= the time in seconds \text{(s)}
C=C_0 e^{-\lambda t}
- C= the count rate at a given time (t) (\text{s}^{-1}\text{, min}^{-1}\text{ or hour}^{-1} \text{ etc})
- C_0= the initial count rate (\text{s}^{-1}\text{, min}^{-1}\text{ or hour}^{-1} \text{ etc})
- \lambda = the decay constant per second \text{(s}^{-1}\text{)}
- t= time in seconds \text{(s)}
Example: A source contains 6 \times 10^{24}. If the decay constant of 2.1 \times 10^{-6} \text{ s}^{-1}, calculate the activity of the source after 1 year.
[4 marks]
Convert 1 year to seconds:
t= \textcolor{ffad05}{1 \text{ year}} = 1 \times 365 \times 24 \times 60 \times 60 = \textcolor{f95d27}{\bold{31 \, 536 \, 000} \textbf{ s} }
Calculate the initial activity:
\begin{aligned} A &= \lambda N \\ A_0 &= \textcolor{00bfa8}{2.1 \times 10^{-6}} \times \textcolor{d11149}{6 \times 10^{24}}) \\ &= \textcolor{aa57ff}{\bold{1.26 \times 10^{19}}} \textbf{ Bq} \end{aligned}
Substitute values into the equation for decay in activity:
\begin{aligned} \bold{A} &= \bold{A_0 e^{-\lambda t}} \\ &= \textcolor{aa57ff}{1.26 \times 10^{19}} \times e^{-(\textcolor{00bfa8}{2.1 \times 10^{-6}} \times \textcolor{f95d27}{31 \, 536 \, 000}}) \\ &= \bold{2.25 \times 10^{-10}} \textbf{ Bq} \end{aligned}
Half-life
The half-life of a sample is the time taken for the number of radioactive nuclei to halve. Therefore, it could also be defined as the time taken for the activity or count rate to halve. The half-life of a sample can be calculated using the equation:
t_{\dfrac{1}{2}}= \dfrac{ln(2)}{\lambda}
- t_{\dfrac{1}{2}}= the half-life in seconds, minutes, hours, days or years
- \lambda= the decay constant per second \text{(s}^{-1}\text{)}
Example: A source of radiation has a decay constant of 0.04 \text{ s}^{-1}. What is its half life?
Substitute into the equation for half-life:
\begin{aligned} \bold{t_{\dfrac{1}{2}}} &= \bold{\dfrac{ln(2)}{\lambda}} \\ &= \dfrac{ln(2)}{\textcolor{00d865}{0.04}} \\ &= \bold{17.3} \textbf{ s} \end{aligned}
Alternatively, half-life can be calculated graphically. By taking two values for activity (one exactly half of the other) and their corresponding times, the half-life can be found.
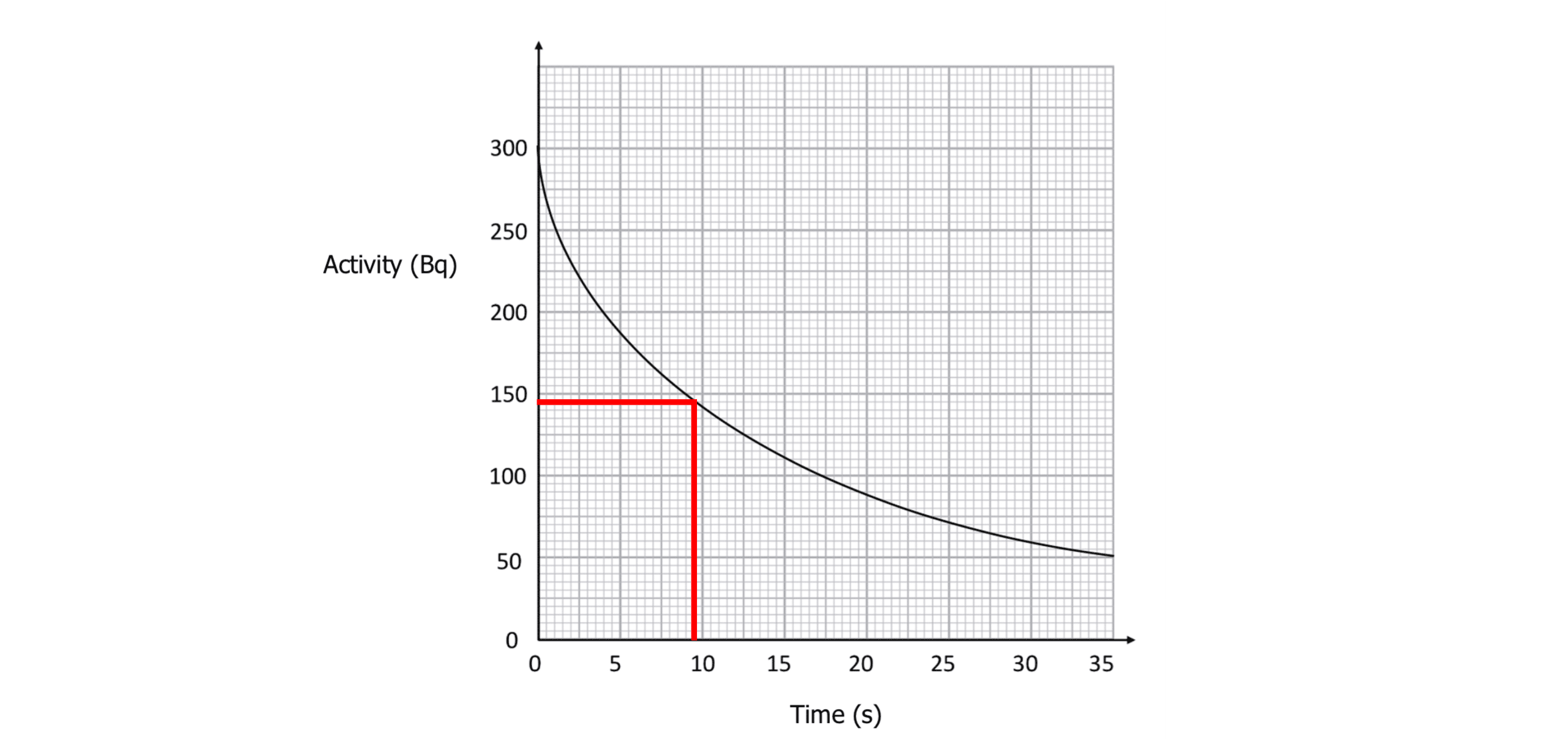
Example: Use the graph to calculate the half-life of this radioactive source.
[2 marks]
Choose two values for activity from the graph, one half the othet:
A_0=290 \text{ Bq and } A_1=145 \text{ Bq}
Read off the corresponding times: = 0 s and 9.5 s
t_0= 0 \text{ s and }t_1=9.5 \text{ s}
Therefore:
\text{half-life}= \bold{9.5} \textbf{ s}
Knowledge of half-life can have some practical applications. For example, carbon-14 is a radioactive isotope with a half-life of 5400 years. By measuring the amount of carbon-14 in an artefact, the artefact can be dated. This is known as carbon dating.
Radioactive Decay Example Questions
Question 1: Over a period of one day, a GM counter detects 6\times 10^6 counts of radiation. What is the activity of the source?
[2 marks]
1 \text{ day} = 24 \times 60 \times 60 = 86400 \text{ s} \\ \begin{aligned} \bold{A} &= \bold{\dfrac{\Delta N}{\Delta t}} \\ &= \dfrac{6 \times 10^6}{86400} \\ &= \bold{69.4} \textbf{ Bq}\end{aligned}
Question 2: State what is meant by the half-life of a radioactive sample?
[1 mark]
The time taken for the number of nuclei/activity/count rate to decrease by half.
Question 3: A radioactive source has a half-life of 20 \text{ s}. Calculate its decay constant.
[2 marks]









