Projectile Motion
Projectile Motion Revision
Projectile Motion
Instead of objects moving in a straight line, often we observe projectiles and perform calculations on them. This section looks at projectiles in motion and drag forces that affect projectiles.
Horizontal and Vertical Components of Motion
When performing calculations on projectiles, it is important to look at the motion vertically and horizontally independently.
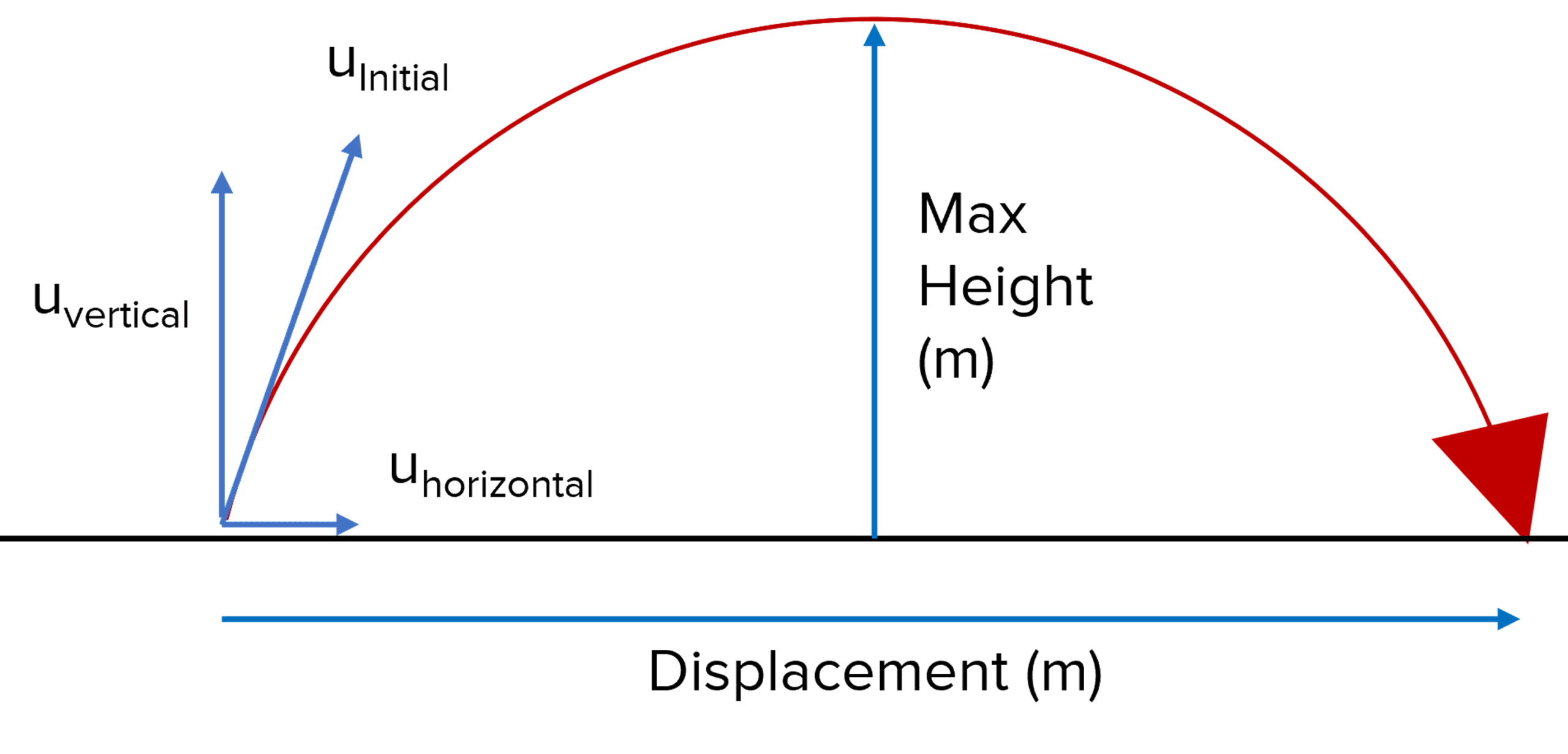
The vertical motion of a projectile determines the maximum height reached, the time in flight and therefore contributes to the overall distance a projectile flies.
The horizontal motion of the projectile purely influences the distance the projectile moves in flight.
The only force acting on the projectile is gravity (as most questions ask you to ignore drag forces).
Before performing calculations on projectiles, it is important to resolve the projectile’s velocity into its horizontal and vertical components. Trigonometry can be used to resolve vectors. Then we can use SUVAT in our calculations.
Drag Forces
Drag forces are forces that oppose the motion of an object. Drag forces always act in the opposite direction to motion and slow an object down. In the process, they usually convert kinetic energy into heat and sound. The two drag forces we need to discuss and learn are friction and air resistance.
Friction is the drag force that occurs when two surfaces rub against one another. Friction always increases as the speed of the object increases and is higher in heavier objects. You can reduce the effects of friction by lubricating surfaces or using smoother materials.
When discussing motion in a straight line on the ground, friction will always cause acceleration, velocity and distance travelled to be lower than calculated and work done to be higher than calculated.
Air resistance is caused when the particles of the air interact with the object moving through it. As the object collides with the air particles, it transfers some of its kinetic energy to the air particles as heat and sound. Air resistance can be reduced by streamlining the object, flying at a higher altitude or reducing speed.
When discussing projectile motion, air resistance will always cause the vertical displacement and horizontal displacement to be lower than our calculated value.
Example: Calculations involving projectiles
A golf ball is hit so that it leaves the ground at an angle of 30° to the horizontal. It leaves the floor with a velocity of 35 \: \text{ms}^{-1}. Calculate how far the ball will travel before hitting the ground. Ignore the effects of drag forces.
[5 marks]
Step 1: Resolve the velocity into its horizontal and vertical components.
\text{Horizontal} = \textcolor{bd0000}{35} \cos \textcolor{7cb447}{30 \degree} = \boldsymbol{30.31} \: \textbf{ms}^{-1}
\text{Vertical} = \textcolor{bd0000}{35} \sin \textcolor{7cb447}{30 \degree} = \boldsymbol{17.5} \: \textbf{ms}^{-1}
Step 2: Determine the time in flight using SUVAT.
Time of flight is determined by vertical motion only. Therefore we only need to consider the vertical motion of the golf ball.
\begin{aligned}S &= \: ? \\ U &= 17.5 \: \text{ms}^{-1} \\ V &= 0 \\ A &= -9.81 \: \text{ms}^{-2} \\ T &= \: ? \end{aligned}
We know V = 0 because at the top of the flight, the vertical velocity is momentarily 0 \: \text{ms}^{-1}.
The acceleration is negative as it is opposing the motion.
We want to find t, the time. We can use v = u + at in this instance.
0 = 17.5 + \left(-9.81 \times t\right)
Rearranging this gives:
9.81 \times t = 17.5
t = \dfrac{17.5}{9.81} = \boldsymbol{1.784} \: \textbf{s}
This is only the time to reach max height so we need to double this for the falling down part of the flight. Therefore:
t = 1.784 \times 2 = \boldsymbol{3.568} \: \textbf{s}
Step 3: Using our time and horizontal velocity, we can determine distance using v = \dfrac{s}{t}.
s = v \times t
s = 30.31 \times 3.568 = 108.14 \: \text{m}
s = \boldsymbol{110} \: \textbf{m}
Projectile Motion Example Questions
Question 1: What forces are acting on an object in projectile motion when drag forces are negligible?
[1 mark]
The only force acting on an object in projectile motion is gravity (or the object’s own weight).
Drag forces are considered negligible for projectile motion questions.
Question 2: A golf ball is hit so that it leaves the ground at an angle of 22 \degree to the horizontal. It leaves the floor with a velocity of 75 \: \text{ms}^{-1}. Calculate the maximum height of the ball. Ignore the effects of drag forces.
[3 marks]
S= \: ? (This is what we are looking)
U= 28.1 \: \text{ms}^{-1}
V= \: 0 \: \text{ms}^{-1} (at the top of the flight, the vertical velocity is momentarily 0 \: \text{ms}^{-1})
A= -9.81 \: \text{ms}^{-2} (minus as the acceleration is opposing motion)
T= \: ? (not needed)
v^2 = u^2 + 2as
u = 0 \: \text{ms}^{-1} so v^2 = 2as .
\begin{aligned} s &= \dfrac{v^2}{2a} \\ \\ s &= \dfrac{28.1^2}{2 \times -9.81} \\ \\ s &= \dfrac{789.61}{-19.62} = \boldsymbol{40.2} \: \textbf{m} \end{aligned}Question 3: What effect do drag forces have on projectiles compared to our calculated theoretical answers?
[2 marks]
Drag forces will always reduce our values from our calculations. Distance, and height will all be lower when drag forces are accounted for.
Projectile Motion Worksheet and Example Questions
SUVAT Questions
A LevelOfficial MMEYou May Also Like...
MME Learning Portal
Online exams, practice questions and revision videos for every GCSE level 9-1 topic! No fees, no trial period, just totally free access to the UK’s best GCSE maths revision platform.
