Nuclear Radius

As seen previously, if a beam of alpha particles are fired at a sheet of gold foil, some of the alpha particles will reflect back to the source. The reason for this phenomenon is the electrostatic repulsion between the positive alpha particle and the positive nucleus. 

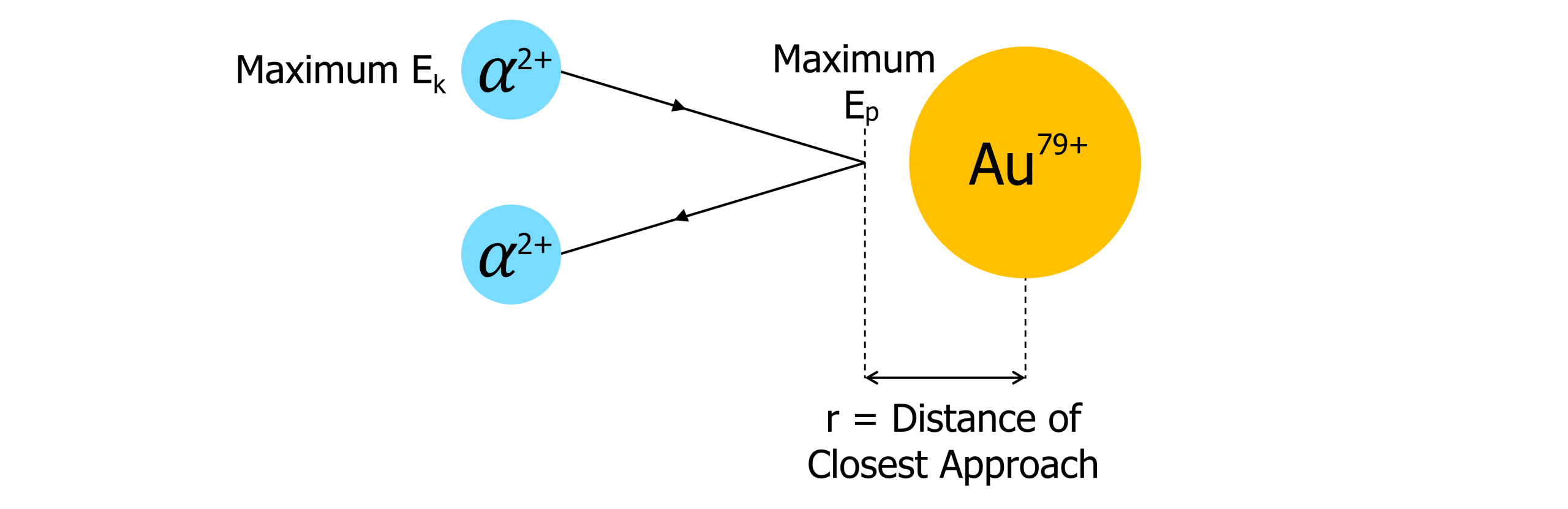
At the point of closest approach, the maximum kinetic energy of the alpha particle must equal the maximum electric potential energy. Therefore:

\begin{aligned} E_k &=E_p \\ E_k &= \dfrac{1}{2}mv^2 \\ E_p &= \dfrac{Qq}{4\pi \epsilon_0 r} \end{aligned}

Hence:

\dfrac{1}{2}mv^2 = \dfrac{Qq}{4 \pi \epsilon_0 r}

r = \dfrac{Qq}{2 \pi \epsilon_0 m v^2}

• Q= the charge of the nucleus in coulombs \text{(C)}
• q= the charge of an alpha particle in coulombs (= 3.2 \times 10^{-19} \text{ C})
• \epsilon_0= the permittivity of free space (= 8.85 \times 10^{-12} \text{s}^4 \text{A}^2 \text{m}^{-3} \text{kg}^{-1}) 
• m= the mass of an alpha particle in kilograms \text{(kg)}
• v= the velocity of the alpha particle in metres per second (\text{ms}^{-1})

Although this method gives an accurate value for the distance of closest approach, it does not give the exact radius of the nucleus. This is because the value includes the distance between the alpha particle and the nucleus which do not touch. Therefore the value will always be an overestimate. 

Some typical values for nuclear radius are shown in the table below:

Element	Nuclear Radius (m)
Carbon	2.66 \times 10^{-15}
Iron	4.35 \times 10^{-15}
Lead	6.66 \times 10^{-15}

 

If a beam of electrons are fired at a diffraction grating at speeds close to the speed of light, they act like a wave and diffract with a de Broglie wavelength equal to:

\lambda = \dfrac{h}{mv}

• \lambda= the de Broglie wavelength in metres \text{(m)}
• h= Planck’s constant (= 6.63 \times 10^{-34} \text{ kgm}^2\text{s}^{-1})
• m= the mass of an electron (=9.11 \times 10^{-31} \text{ kg})
• v= the velocity of the electron in metres per second \text{(ms}^{-1})

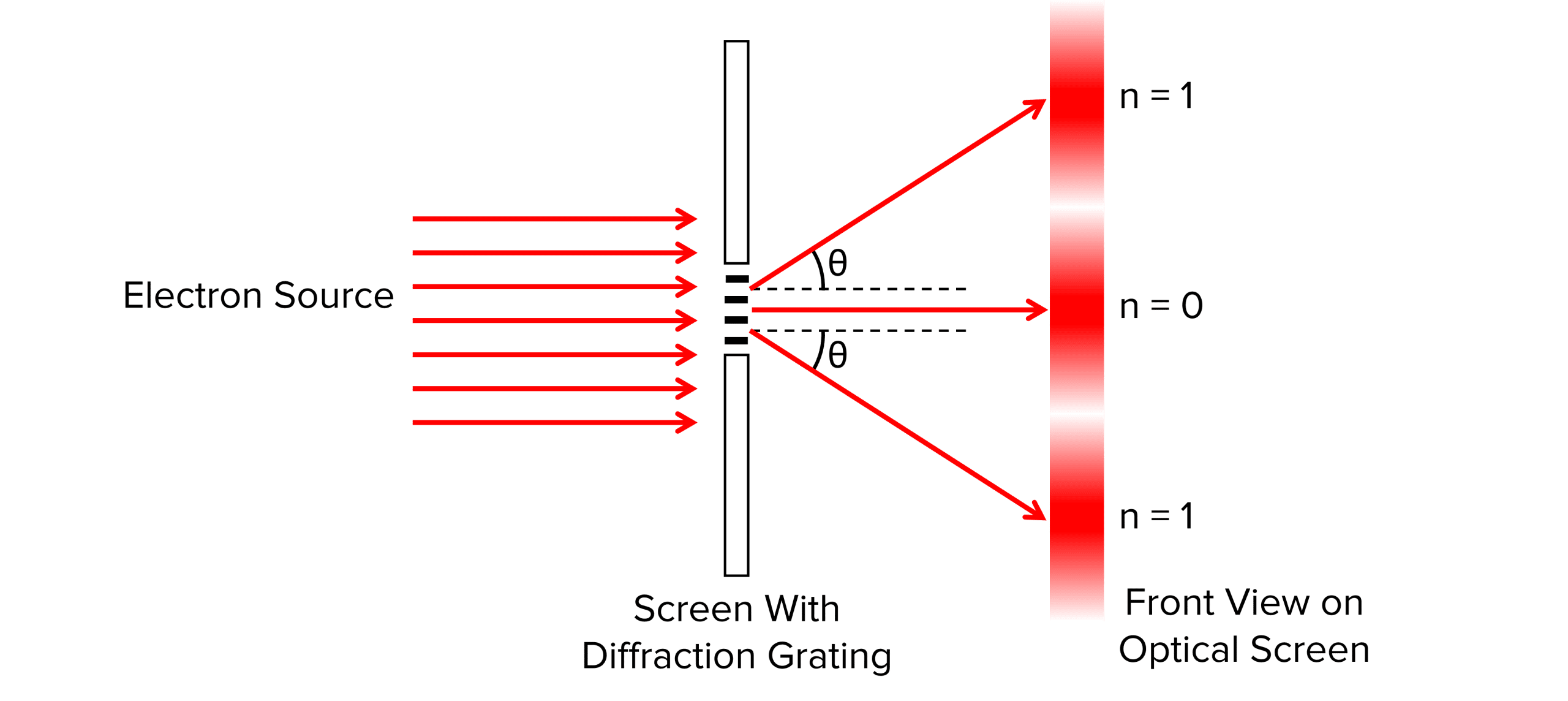
If the electron is passed through the diffraction grating it forms a pattern of concentric rings made of minima and maxima on a screen. By measuring the angle to the first minima, the radius of a nucleus can be calculated using:

R= 1.22 \dfrac{\lambda}{2 Sin \theta}

• \lambda= the de Broglie wavelength in metres \text{(m)}
• \theta = the angle to the first minimum in degrees or radians \degree \text{ or rad})

This method gives a very accurate, direct measurement for the radius of the nucleus. However, for this method to work the electrons must be close to the speed of light which can be difficult to achieve. 

A graph of diffraction angle against intensity of electrons can be plotted:

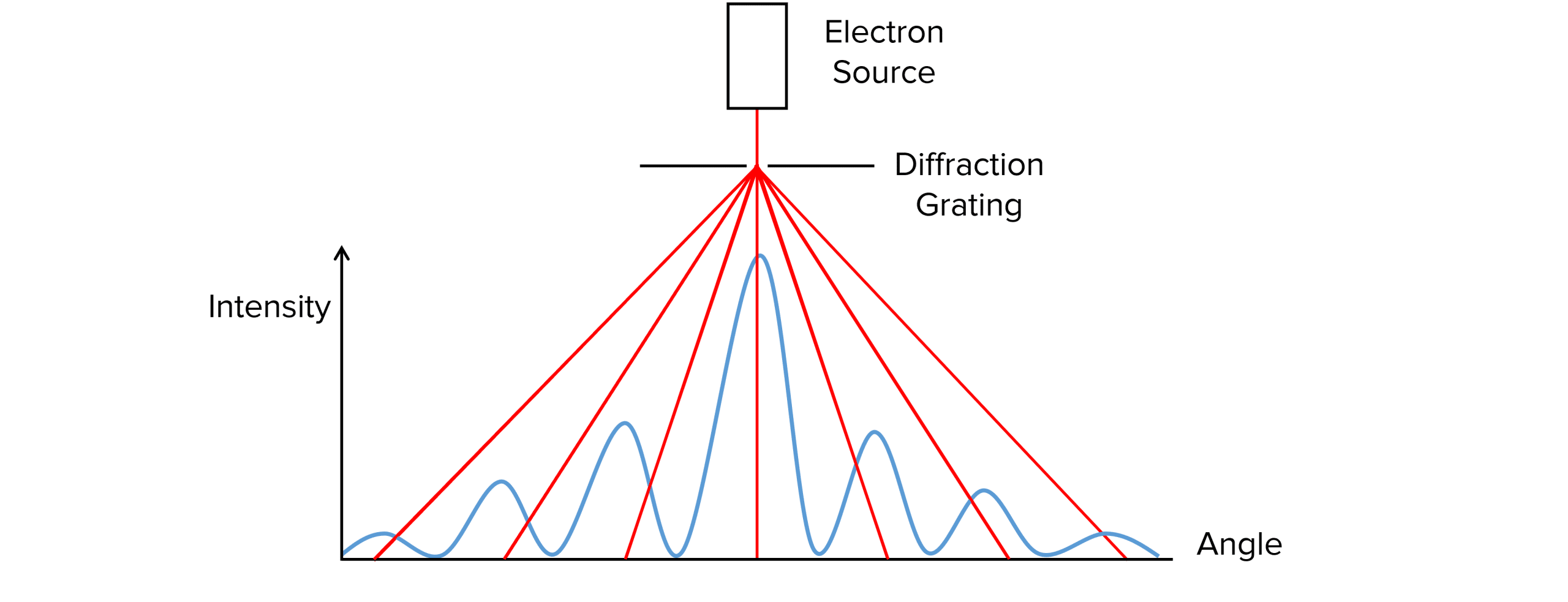
The first minima can be found as the minima closest to the central maxima. On a graph of intensity against angle, the angle can be determined and placed in the equation above to calculate nuclear radius. 

Through repeated experimentation with different atoms, an equation for calculating the nuclear radius was formed. 

R=\dfrac{1}{3} R_0 A

• R= the nuclear radius in metres \text{(m)}
• R_0= a constant of proportionality (=1.05 \text{ fm})
• A= the mass number of the atom

Example: Calculate the nuclear radius of carbon-12.

[2 marks]

\begin{aligned} \bold{R} &= \bold{\dfrac{1}{3} R_0 A} \\ &= \dfrac{1}{3} 1.05 \times 10^{-15} \times 121 \\ &= \bold{2.4\times 10^{-15}}\textbf{ m} \end{aligned}

 

Assuming the nucleus is a sphere, it’s volume can be calculated using the equation:

V=\dfrac{4}{3} \pi R^3

• V= volume in cubic metres \text{(m}^3)
• R= the nuclear radius in metres \text{(m)}

We have just learnt that the nuclear radius can be calculated using R=\dfrac{1}{3}R_0 A. Sunstituting this into the above equation gives:

\begin{aligned}V &= \dfrac{4}{3} \pi (\dfrac{1}{3} \pi R_0 A)^3  \\ V &= \dfrac{4}{3} R_0^3 A \end{aligned}

 

As density is the mass per unit of volume and:

\rho = Au

• \rho= density in kilograms per cubic metre \text{kgm}^{-1}
• A= the atomic number
• u= the atomic mass unit (=1.66 \times 10^{-27} \text{ kg})

Therefore:

\begin{aligned} \rho &=\dfrac{Au}{\dfrac{4}{3}\pi R_0^3 A} \\ \rho &= \dfrac{3u}{4 \pi R_0^3} \end{aligned}