Mass and Energy
Mass and Energy Revision
Mass and Energy
E=mc^2 is an equation most people have heard of but many may not know it’s meaning or relevance. In this section we look at this equation and the link between energy and mass.
Mass-Energy Equivalence
While experimenting on his famous theory of relativity, Einstein proposed mass and energy can be considered equivalent and are interchangeable.
This idea is represented by the equation:
E=mc^2
- E= energy in joules \text{(J)}
- m= mass in kilograms \text{(kg)}
- c= the speed of light (=3\times 10^8 \text{ ms}^{-1})
The most useful practice from this is the ability to convert mass to energy. For a small amount of mass, a huge amount of energy can be produced due to the c^2 in the equation.
Because of the production of huge amounts of energy, the mass-energy equivalence can be put to use in nuclear weapons and nuclear power, nuclear fusion in the sun and high energy collisions in particle accelerators.
Atomic Mass Unit
The atomic mass unit (u) is often used in nuclear physics instead of dealing with incredibly small masses in \text{(kg)}. The a.m.u is equal to \dfrac{1}{12}th of the mass of a carbon-12 atom. The conversion you need to use is: (this is given on your data sheet)
1 \text{ u}=1.661 \times 10^{-27} \text{ kg}
Example: An electron has a mass of 5.5 \times 10^{-4} \text{ u}. Convert this mass to kilograms.
[1 mark]
1 \text{ u} = 1.66 \times 10^{-27} \text{ kg} \\ \textcolor{10a6f3}{5.5 \times 10^{-4}} \times 1.661 \times 10^{-27} = \bold{9.1355 \times 10^{-31}} \textbf{ kg}
Mass Defect
When scientists measured the mass of the nucleus of an atom as a whole and then they measured the mass of the nucleus separated into its constituents and compared the two, they found that the mass of a nucleus as a whole was always less than the mass of its constituents. They named the difference in mass the mass defect.
The diagram below shows a representation of carbon-12 as a whole nucleus on the left and separated into protons and neutrons on the right. If measured, the mass of the nucleus on the left will always be less than the mass of the protons and neutrons on the right. The difference is the mass defect of carbon-12.
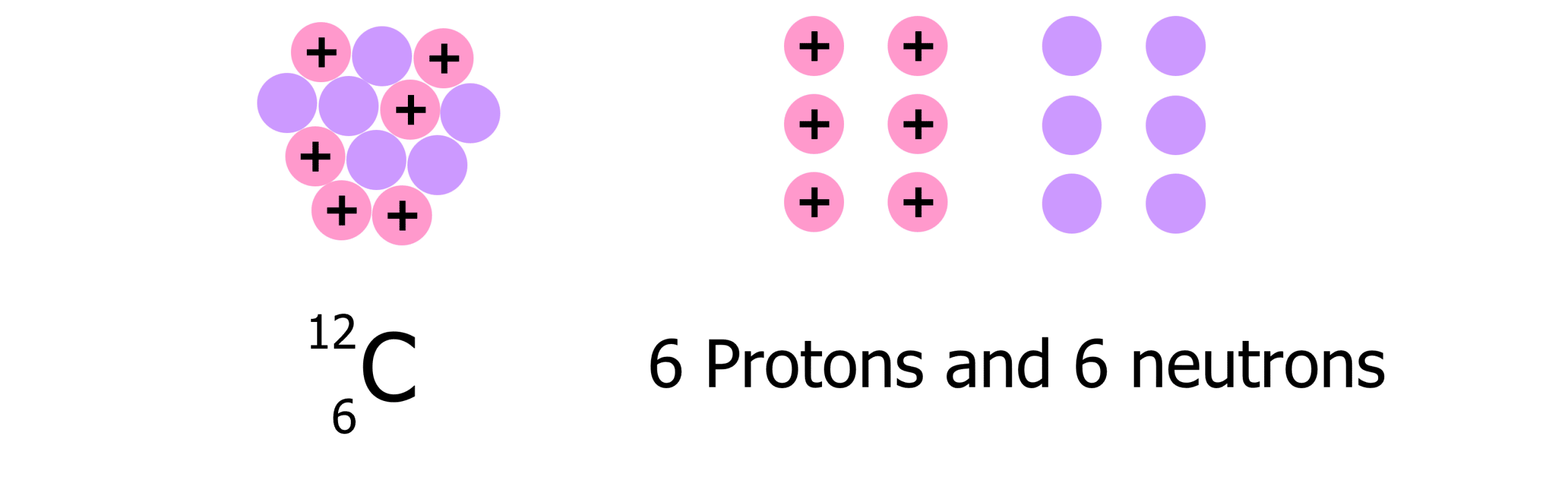
The mass defect (\Delta m) can be calculated using the equation:
\Delta m= Z m_p + (A-Z) m_n - m_{\text{total}}
- \Delta m= the mass defect in kilograms \text{kg})
- Z= the number of protons
- m_p= the mass of a proton (=1.67 \times 10^{-27} \text{ kg}=1.00728 \text{ u})
- A= the nucleon number
- m_n= the mass of a neutron (= 1.67 \times 10^{-27} \text{ kg} = 1.00867 \text{ u})
- m_{\text{total}}= the mass of the nucleus as a whole
This equation can be simplified to:
\text{mass defect}=\text{total mass of protons} + \text{total mass of neutrons} - \text{total mass of the nucleus as a whole}
Example: The mass of iron-56 is 55.845 \text{ u}. Calculate the mass defect of iron-56. Give your answer in kilograms.
[3 marks]
Find A and Z for iron-56:
Z=26 (from datasheet)
A=\textcolor{7cb447}{56}-26=30Substitute into the mass defect equation:
\begin{aligned} \bold{\Delta m} &= \bold{Z m_p + (A-Z) m_n - m_{\text{total}}} \\ &= (26 \times 1.00728)+(30\times 1.00867) - \textcolor{ffad05}{55.845} \\ &= 0.6043 \text{ u} \\ &= \bold{0.06043 \times 1.661 \times 10 {-27}} \\ &= \bold{1.0039 \times 10^{-27}} \textbf{ kg} \end{aligned}
Binding Energy
Binding energy is the energy needed to separate a nucleus into its components. The mass of the components is always greater than the mass of the nucleus as an energy input is needed to separate the nucleus into its components, and mass and energy are interchangeable. Therefore the input of energy needed to separate the components becomes the gain in mass.
This also means that when a nucleus is formed, the equal but opposite amount of energy is released. The amount of energy can be calculated using the equation:
E=\Delta m c^2
- E= energy in joules \text{(J)}
- \Delta m= change in mass in kilograms \text{(kg)}
- c= the speed of light (=3 \times 10^8 \text{ms}^{-1})
Example: Using the previous example, calculate the binding energy per nucleon (\dfrac{E}{A})of iron-56. \Delta m = 1.0039 \times 10^{-27} \text{ kg}.
[2 marks]
\begin{aligned} \bold{E} &= \bold{\Delta mc^2} \\&= \textcolor{aa57ff}{1.0039 \times 10^{-27}} \times (3\times 10^8)^2 \\ 9.035 \times 10^{-11} \text{J} \\ \dfrac{E}{A} &= \dfrac{9.035 \times 10^{-11}}{\textcolor{f95d27}{56}} \\ &= \bold{1.6 \times 10^{-12}} \textbf{ J} \end{aligned}
Mass and Energy Example Questions
Question 1: What is the mass defect and how is it calculated?
[2 marks]
The difference in mass between the nucleus of an atom and the mass of its constituents when separated.
\bold{\Delta m = Z m_p + (A-Z)m_n - m_{\text{total}}}where:
- \Delta m is the mass defect
- Z is the number of protons
- m_p is the mass of a proton
- A is the nucleon number
- m_n is the mass of a neutron
- m_{\text{total}} is the mass of the nucleus as a whole
Question 2: The mass of carbon-12 is 12.011 \text{ u}. Calculate the mass defect of carbon-12. (Mass of proton =1.00728 \text{ u} and mass of a neutron =1.00867 \text{ u}
[3 marks]
Question 3: Define the binding energy of a nucleus.
[1 mark]
Binding energy is the energy needed to separate a nucleus into its components.
You May Also Like...

MME Learning Portal
Online exams, practice questions and revision videos for every GCSE level 9-1 topic! No fees, no trial period, just totally free access to the UK’s best GCSE maths revision platform.