Ideal Gases

Commonly, temperature is measured in degrees Celsius (\degree C) which is appropriate for measuring everyday temperatures. 

However, in thermodynamics another scale is used for measuring temperature which is known as the Kelvin Scale. The Kelvin Scale begins at 0 \text{ K} which is known as absolute zero and increases from there. There are no negative numbers in the Kelvin Scale as absolute zero (0 \text{ K}) is the lowest possible temperature. 

Absolute zero (0 \text{ K}) is the point at which all particles stop vibrating and therefore, have zero kinetic energy. It is no longer possible to remove energy and therefore, temperature cannot decrease further. 

0 \text{ K} is equal to -273.15 \degree C and every increase by 1\degree C corresponds to an increase in 1 \text{ K}. 

To convert from degrees Celsius to Kelvin:

T\text{ (K)}= T \, (\degree C) + 273.12

• T\text{ (K)}= the temperature in kelvin \text{(K)}
• T \, (\degree C)= the temperature in degrees Celsius (\degree C)

Example: The temperature at a point in space is measured to be -270 \degree C. Convert this temperature to Kelvin.

[1 mark]

\begin{aligned} T\text{ (K)} &= T \, (\degree C) + 273.15 \\ &= \textcolor{00d865}{-270} + 273.15 \\ &= \bold{3.15} \textbf{ K} \end{aligned}

There are three key gas laws which describe the relationship between pressure, temperature and volume.

Boyle’s Law:

Boyle’s law states that the pressure (P) of a gas is inversely proportional to the volume (V) for a gas of constant temperature.

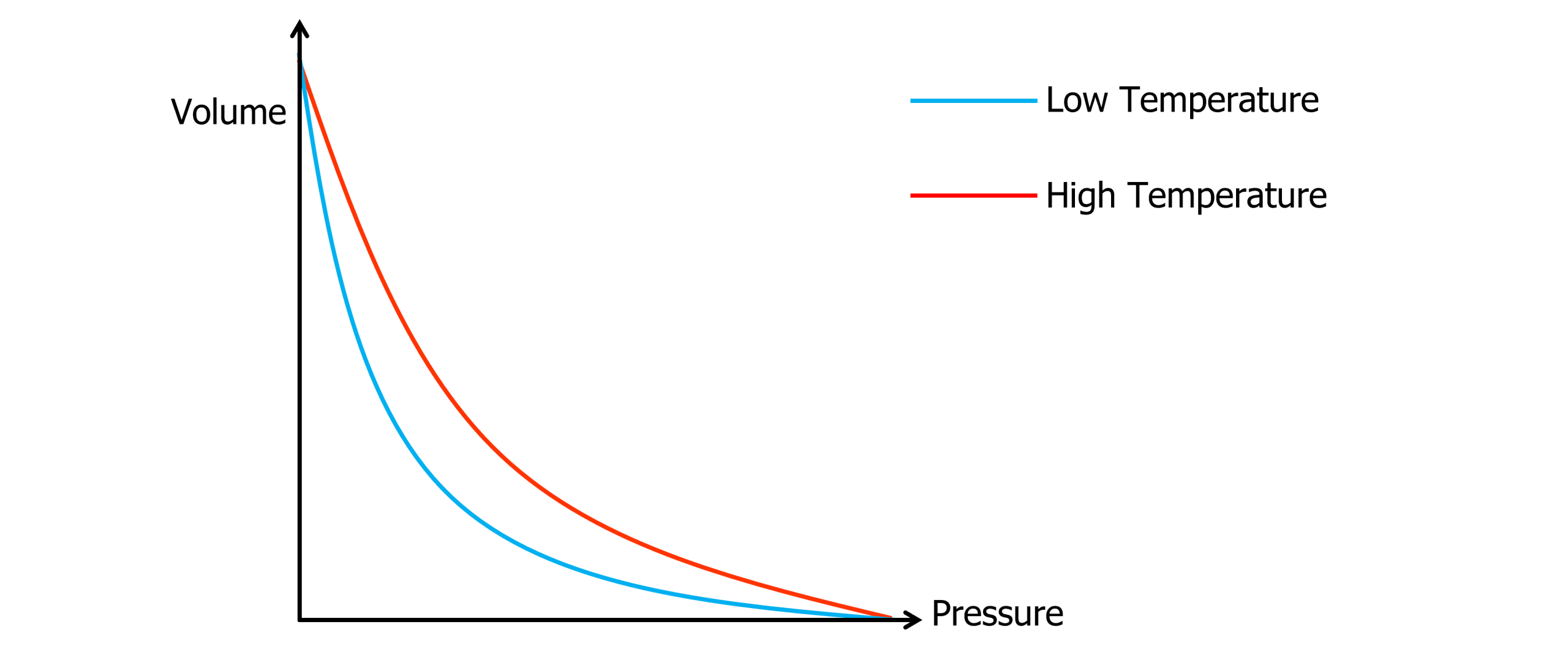
P \propto \dfrac{1}{V}

• P= pressure in pascals \text{(Pa)}
• V= volume in cubic metres \text{(m}^3\text{)}

This can also be written experimentally as:

P_1V_1=P_2V_2

• P_1= the initial pressure in pascals \text{(Pa)}
• V_1= the initial volume in cubic metres \text{(m}^3\text{)}
• P_2= the final pressure in pascals \text{(Pa)}
• V_2= the final volume in cubic metres \text{(m}^3\text{)}

Or

PV=\text{constant}

Example: A 0.1 \text{m}^3 piston contains a gas under 100 \text{ Pa} of pressure. The volume of the pressure is reduced to 0.02 \text{ m}^3 piston. Calculate the new pressure assuming the temperature remains constant. 

[2 marks]

\begin{aligned} \bold{P_1V_1} &= \bold{P_2V_2} \\ P_2 &= P_1 \dfrac{V_1}{V_2} \\ &= \textcolor{7cb447}{100} \times \dfrac{\textcolor{f95d27}{0.1}}{\textcolor{10a6f3}{0.2}} \\ &= \bold{500} \text{ Pa} \end{aligned}

Charles’s Law:

Charles’s Law states that the volume of a gas is proportional to the temperature of the gas for a gas at constant pressure.

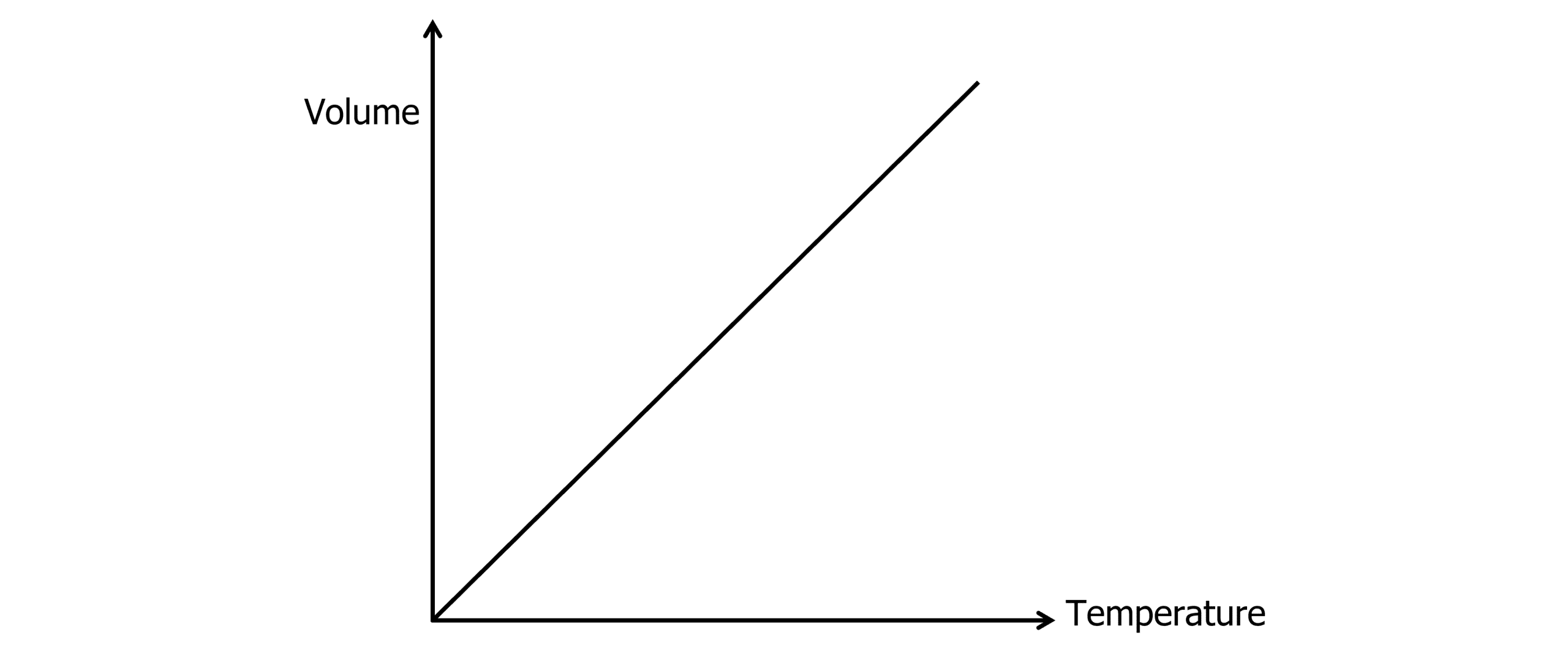
V \propto T

• V= volume in cubic metres \text{(m}^3\text{)}
• T= temperature in kelvin \text{(K)}

This may also be written experimentally as:

\dfrac{V_1}{T_1} = \dfrac{V_2}{T_2}

• V_1= the initial volume in \text{(m}^3\text{)}
• T_1= the initial temperature in kelvin \text{(K)}
• V_2= the final volume in \text{(m}^3\text{)}
• T_2= the final temperature in kelvin \text{(K)}

Example: A container contains a gas of a fixed pressure. The initial volume of the container is 0.2 \text{ m}^3 at a temperature of 25 \degree C. The container is heated to 75 \degree C. What is the new volume of the container?

[2 marks]

\begin{aligned} \bold{\dfrac{V_1}{T_1}} &= \bold{\dfrac{V_2}{T_2}} \\ V_2 &= V_1 \times \dfrac{T_2}{T_1} \\ &= \textcolor{10a6f3}{0.2} \times \dfrac{\textcolor{7cb447}{75+273}}{\textcolor{ffad05}{25+273}}&= \bold{0.23} \textbf{m} \bold{^3} \end{aligned}

Pressure Law: 

The Pressure Law states for a fixed volume of gas, pressure and temperature are proportional. 

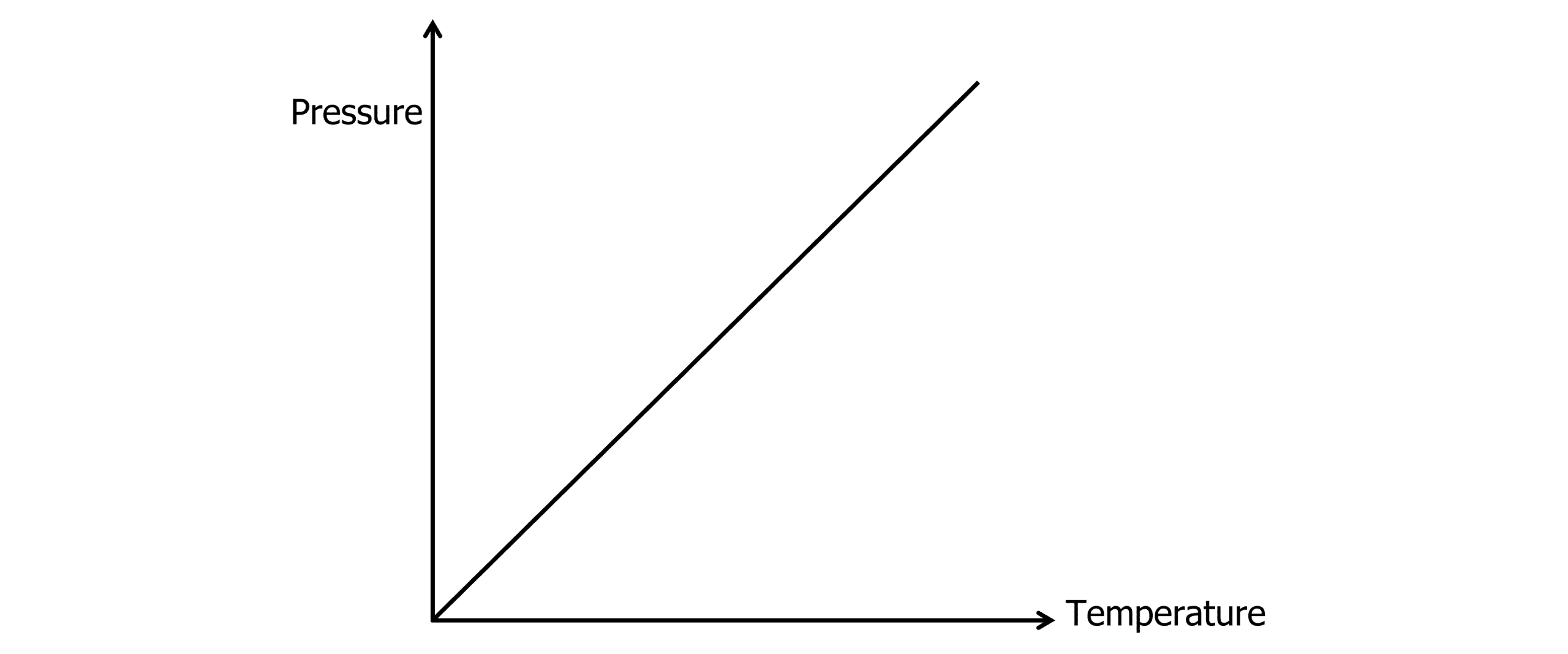
P \propto T

• P= pressure in pascals \text{(Pa)}
• T= temperature in kelvin \text{(K)}

This may also be written experimentally as:

\dfrac{P_1}{T_1}=\dfrac{P_2}{T_2}

• P_1= the initial pressure in pascals \text{(Pa)}
• T_1= the initial temperature in kelvin \text{(K)}
• P_2= the final pressure in pascals \text{(Pa)}
• T_2= the final temperature in kelvin \text{(K)}

Example: A fixed volume of gas is stored at 10\degree C under a pressure of 250 \text{ Pa}. The container is cooled to 5 \degree C. Calculate the new pressure inside the container.

[2 marks] 

\begin{aligned} \bold{\dfrac{P_1}{T_1}} &= \bold{\dfrac{P_2}{T_2}} \\ P_2 &= P_1 \dfrac{T_1}{T_2} \\ &= \textcolor{f95d27}{250} \times \dfrac{\textcolor{7cb447}{5 + 273}}{\textcolor{00bfa8}{10+273}} \\ &= \bold{246} \textbf{ Pa} \end{aligned}

It is important to note that real gases do not follow these ideal gas laws. The ideal gas laws rely upon certain assumptions. These assumptions (which are listed later in this page) are not met by real gases. 

An ideal gas is a gas that follows all three gas laws. These combine form a new equation:

PV \propto T

Or written as an equation:

PV=kT

• P= pressure in pascals \text{(Pa)}
• V= volume in cubic metres \text{(m}^3\text{)}
• k= a constant of proportionality 
• T= temperature in kelvin \text{(K)}

An ideal gas consists of molecules moving around in random directions, at high speeds. The molecules collide with each other and the walls of the container, exerting an outwards force on the container. The kinetic energy of each particle is represented below. The molecules are moving in random directions with different amounts of kinetic energy. 

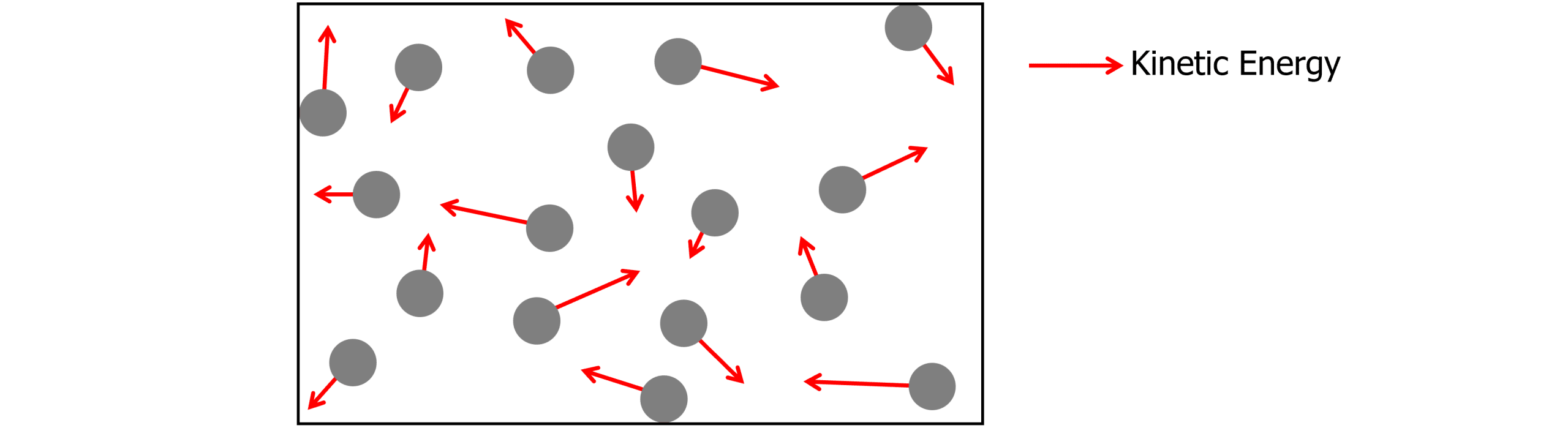
As the temperature increases, the kinetic energy of each particle increases. Therefore, the molecules collide with the containers with more energy and more frequently, increasing the pressure. 

Similarly, if the volume of the container is decreased, the molecules collide with the container more often, and therefore increasing pressure. 

Doing the experiment:

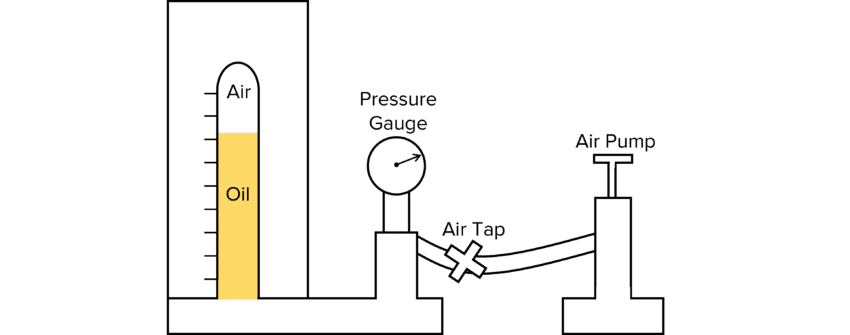
1. Set up the experiment as shown in the diagram. 
2. Ensure there are no leakages when the equipment has been fully set up. If there are, these need to be resolved before starting.
3. Open the air tap and begin pumping air into the cylinder using the air pump.
4. Keep pumping until the oil reaches the upper part of the column.
5. Close the air tap once the oil stops rising and the pressure reading remains constant. 
6. Allow two minutes for the compressed air to cool down to room temperature, then record the pressure and volume in your results table. 
7. Repeat 10 times to collect 10 pairs of readings for pressure and volume. 

Analysis of Results:

If completed correctly, you should find that the product of pressure and volume of each pairs of readings gives a constant:

PV=k

Alternatively, a graph of pairs of readings for P against V could be produced. A linear graph would be produced showing that Boyle’s law had been abided. 

If temperature is not kept constant, the graph will not be linear and Boyle’s law cannot be applied. To keep a constant temperature it is important to keep a constant room temperature and allow the equipment and gas to cool after each trial.