Thermal Energy Transfer

All substances have internal energy (U) which varies depending upon the temperature and state of the substance. Internal energy is made up of both the kinetic energy of the particles in the substance, and the particles potential energy.

Kinetic energy – this is the energy the particles have due to the velocity they are moving within a substance. Gas particles have the greatest kinetic energy and solid particles have the least kinetic energy.

Potential energy – this is the energy a substance has due to the intermolecular forces between particles. As the particles move further apart, the potential energy increases between molecules. 

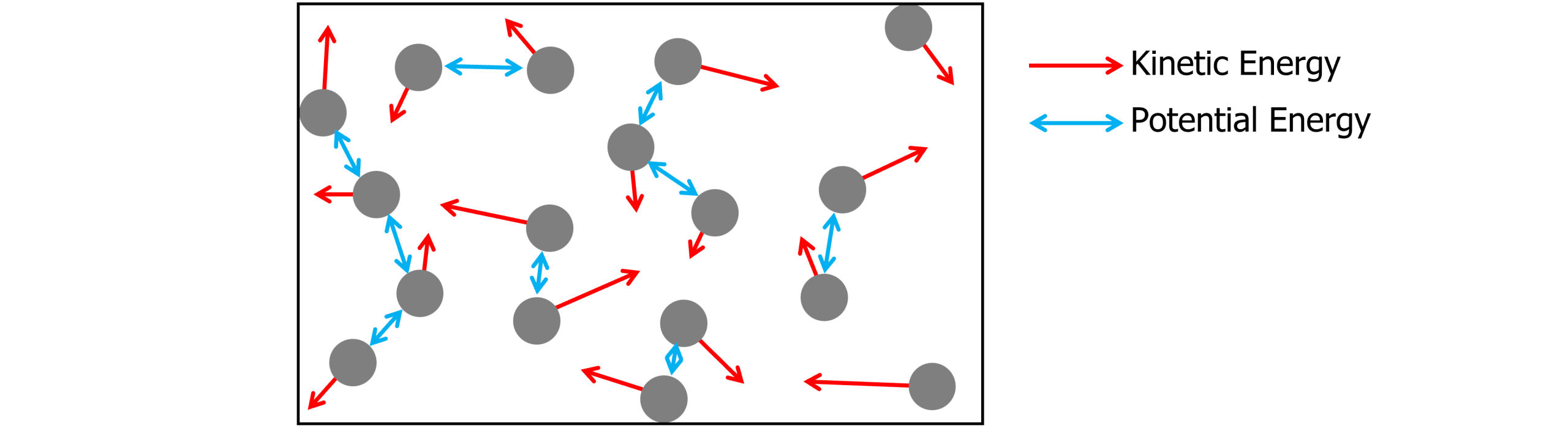
The internal energy of a system is determined by the random motion of the particles in the substance, their kinetic energy (temperature), state of matter and the intermolecular forces between particles. 

To increase the internal energy of a substance, the substance needs to either be heated, or have work done on it. Work done on the gas would usually be in the form of compressing the substance. The opposite would be needed for a decrease in internal energy (reduced temperature or expansion). 

The specific heat capacity of a substance tells us how easy it is to heat the substance. It can be defined as the amount of energy needed to increase the temperature of 1 \text{ kg} of the substance by 1 \text{ K or } 1 \degree C without changing its state. The greater the specific heat capacity, the slower the substance heats up or cools down. 

\Delta Q= mc \Delta \theta

• \Delta Q= the change in thermal energy in joules \text{(J)}
• m= the mass of the substance in kilograms \text{(kg)}
• c= teh specific heat capacity in joules per kilogram per kelvin \text{(Jkg}^{-1}\text{K}^{-1}\text{)}
• \Delta \theta= the change in temperature in kelvin \text{(K)}

Example: The specific heat capacity of water is 4200 \text{ Jkg}^{-1}\text{K}^{-1}. How much energy is needed to heat 12 \text{ kg} of water by 300 \degree C?

[2 marks]

First, calculate the temperature change in kelvin: 

\Delta \theta = \textcolor{2730e9}{300} \degree C = 30 \text{ K}

Substitute values into the equation for change in energy:

\begin{aligned} \bold{\Delta Q} &= \bold{mc\Delta T} \\ &= \textcolor{00d865}{12} \times \textcolor{f95d27}{4200} \times 30 \\ &= \bold{15} \text{ MJ} \end{aligned}

Often you need to calculate the energy transferred to a substance using an electrical heater. Energy can be calculated using the equation:

P=\dfrac{E}{t}

• P= power in watts \text{(W)}
• E= energy transferred in joules \text{(J)}
• t= time in seconds \text{(s)}

Example: A 2 \text{ kW} electric heater is used to heat a substance. The heater is used for 5 minutes. How much energy has been transferred to the substance?

[2 marks]

Calculate the power and time:

\textcolor{10a6f3}{2} \text{ kW} = 2000 \text{ W} \\ \textcolor{ffad05}{5} \text{ mins} = 60 \times 5  =300 \text{ s}

Substitute values into the equation for energy:

\begin{aligned} \bold{E} &= \bold{Pt} \\ &= 2000 \times 300 \\ &= \bold{6} \text{ kJ} \end{aligned} 

When a substance is heated or cooled, it experiences changes of state. When the substance changes state, its internal energy changes but its temperature remains constant. At this point, molecules within the substance move further apart (when increasing energy) or move closer together (when decreasing energy), causing a change in potential energy. As the temperature remains the same, the kinetic energy remains constant. 

The energy required to change the state of 1 \text{ kg} of a substance without changing its temperature is known as the specific latent heat.

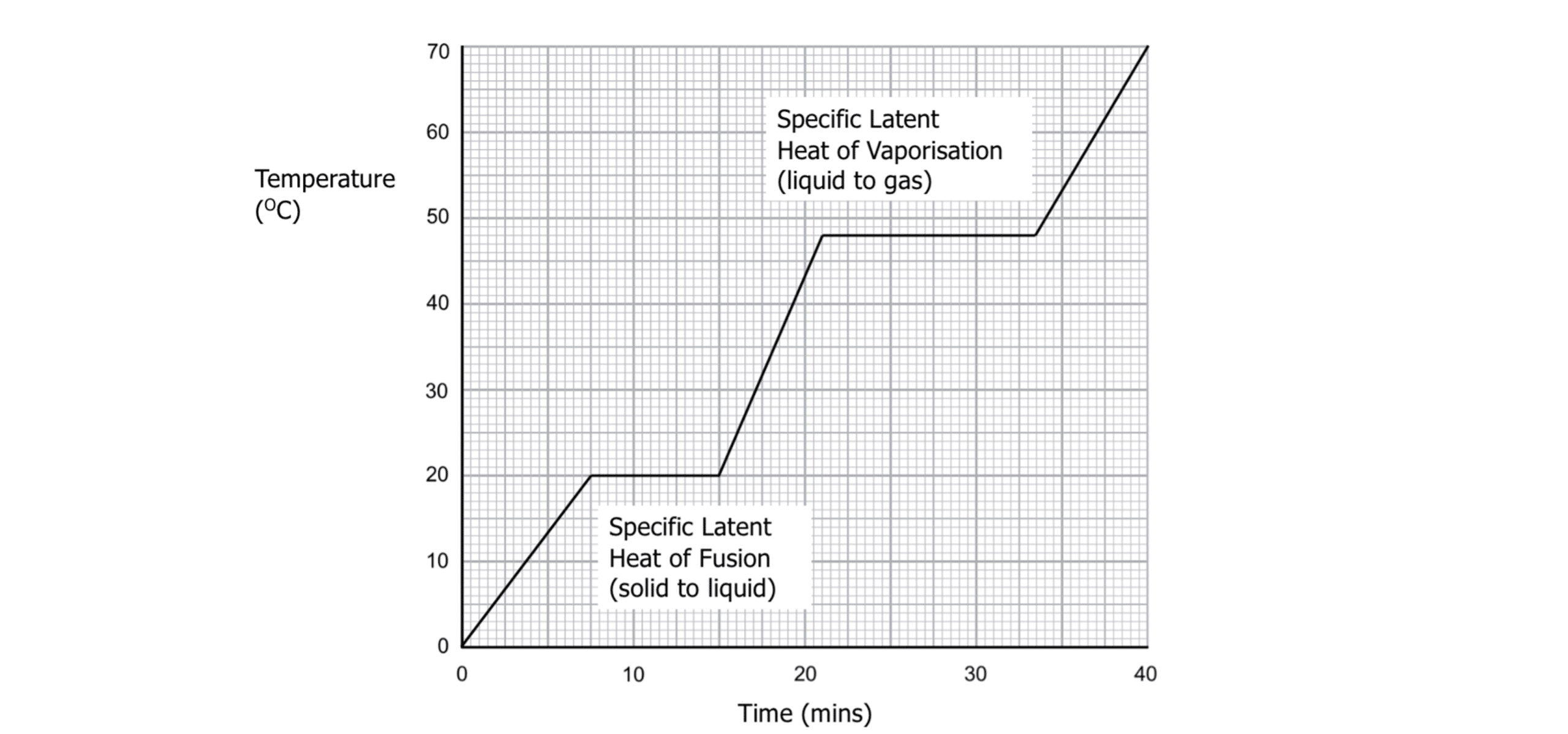
The specific latent heat of fusion is the energy required to change the state of a substance from a solid to a liquid. 

The specific latent heat of vaporisation is the energy required to change the state of a substance from a liquid to a gas. Specific latent heat can be calculated using the equation:

Q=mL

• Q= the energy supplied to change state without a change in temperature in joules \text{(J)}
• m= the mass in kilograms \text{(kg)}
• L= the specific latent heat in joules per kilogram \text{(Jkg}^{-1}\text{)}

Example: Calculate the specific latent heat of 0.5 \text{ kg} of a substance when 0.8 \text{ MJ} are supplied.

[2 marks]

\begin{aligned} \bold{Q} &= \bold{mL} \\ L &= \dfrac{Q}{m} \\ &= \dfrac{\textcolor{10a6f3}{0.8 \times 10^6}}{\textcolor{aa57ff}{0.5}} \\ &= \bold{1.6 \times 10^6} \textbf{ kg}\bold{^{-1}} \end{aligned}