Trigonometry Basics

Standard Trigonometric Values

Below is a table of key angles and corresponding values that you’ll need to know, moving forward.

We want to know these values in exact form, so we aren’t losing any level of accuracy when carrying our values forward.

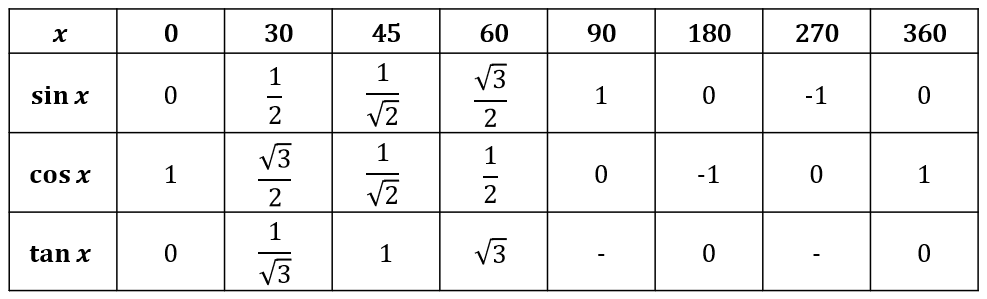
If you’re particularly eagle-eyed, you might notice that the values for 360° are the same as the values at 0° – this is not a coincidence, the graphs for \sin x and \cos x repeat every 360°. The \tan x graph repeats every 180°.

In case you forget…

Here’s a useful way of remembering.

Imagine an equilateral triangle with side length 2\text{ cm}.

Split the triangle in half, and label each side, as below.

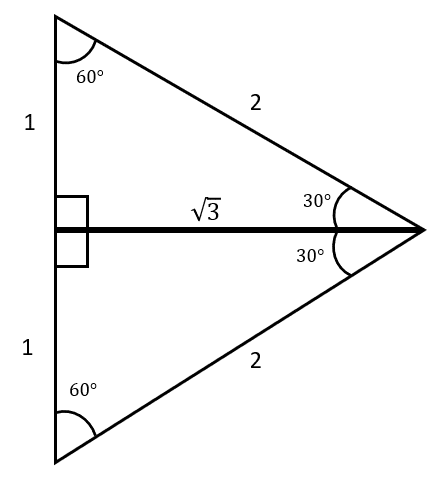
For the angle that you’ve forgotten, select the appropriate two sides to find that angle.

So, for example, let’s say you’ve forgotten the value of \tan 30°.

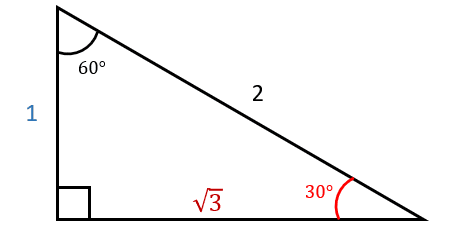
Remember, \tan x = \dfrac{\text{opposite}}{\text{adjacent}}.

So, choose \tan \textcolor{red}{30º} to give \dfrac{\textcolor{blue}{1}}{\textcolor{maroon}{\sqrt{3}}} – easy!

You might’ve also noticed that \tan 90° and \tan 270° don’t have any values. Well, think about the triangle above. If we’re looking to use the opposite and adjacent sides, our opposite is technically the hypotenuse. How, then, would we decide which adjacent side is ‘the adjacent’?

We can’t, so suggest that our system fails at these values.

The Unit Circle

The Unit Circle is a circle of radius 1, which is centred on the origin. Any point on the unit circle has co-ordinates (\cos \theta , \sin \theta ), where \theta is the angle between the positive x axis and the line connecting our point and the origin, in an anticlockwise direction. That can be extended all the way to \theta = 360°, at which point, the circle is repeated.

If that sounds a little confusing, here’s a demonstration.

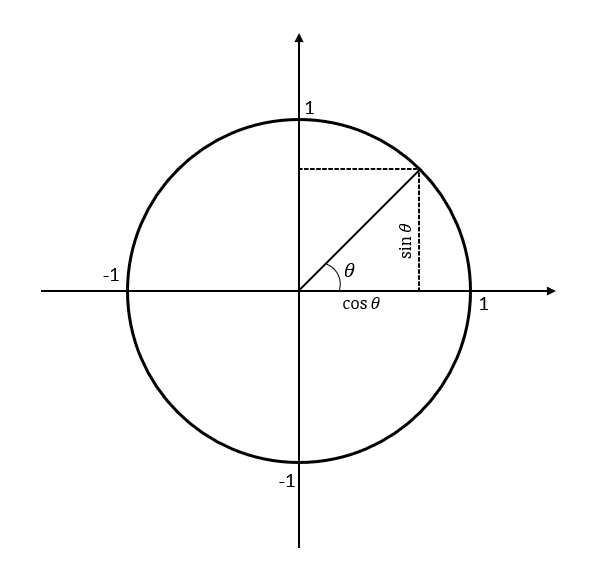
So, let’s say we have \theta = 30°. Then on the unit circle, have the point (\cos 30°, \sin 30°) = \left( \dfrac{\sqrt{3}}{2}, \dfrac{1}{2}\right) , which is exactly 1 unit from the origin.

The Trigonometry Graphs

Here’s a quick demo of the y = \sin x graph…

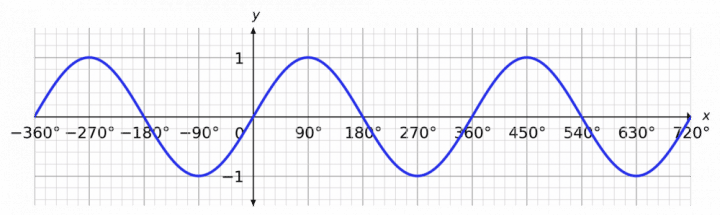
… and the y = \cos x graph…

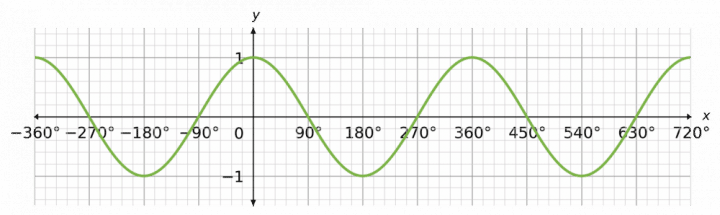
and the y = \tan x graph.

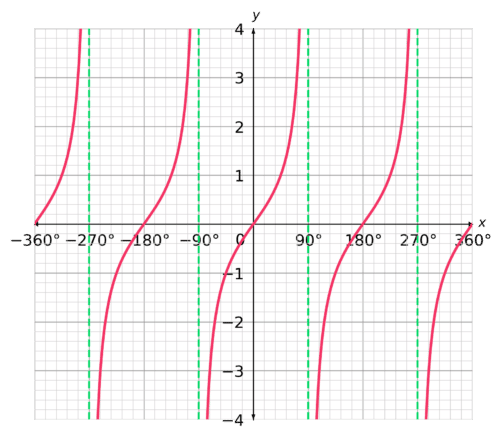
The green indicator lines are along all values of x where \tan x has no value.

They’re known as asymptotes.

Degree – Radian Conversions

Don’t be scared off – radians are just as simple to understand as degrees.

You don’t necessarily need to know all of the conversions, but they’re listed below anyway.

As long as you can remember that \textcolor{red}{2\pi} radians is exactly \textcolor{blue}{360°}, you’ll be able to work out the rest of the conversions.

Where degrees are written with °, we might see radians written \text{rad}, \text{r}, or ^\text{c}.