Revise
Product Moment Correlation Coefficient
Product Moment Correlation Coefficient Revision
Product Moment Correlation Coefficient
The Product Moment Correlation Coefficient (PMCC or sometimes just r) is a number that tells you how correlated your data are. It is always between -1 and 1.
- If it is positive then there is positive correlation, with stronger positive correlation being closer to 1.
- If it is negative then there is negative correlation, with stronger negative correlation being closer to -1.
- If it is 0 then there is no correlation – a number close to 0 is usually an indicator that variables are not correlated too.
You can calculate the Product Moment Correlation Coefficient on your calculator – it will be in the statistical functions.
Note: Linear transformations of x and y, such as S=ax+b, do not affect the Product Moment Correlation Coefficient.
Make sure you are happy with the following topics before continuing.
Hypothesis Testing with the Product Moment Correlation Coefficient
When measuring variables that are not correlated, it is possible that some correlation might arise by chance. A Product Moment Correlation Coefficient hypothesis test is a test to see if variables really are correlated.
The population parameter is \rho, the product moment correlation coefficient of the population.
The test statistic is r, the product moment correlation coefficient of the sample (the data we have).
The hypotheses are always the same:
H_{0}: \rho=0
H_{1}: \rho>0\text{ or }\rho<0 (one tail)
H_{1}: \rho\neq 0 (two tail)
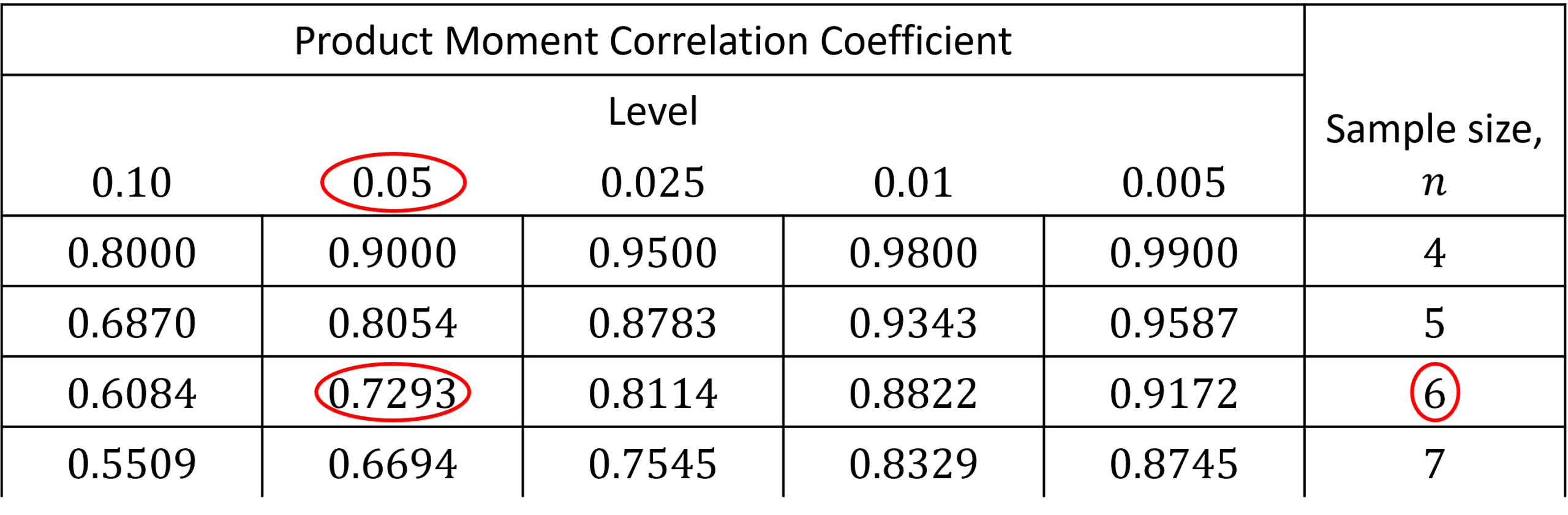
In your formula booklet there will be a table against which you test your test statistic. For example, if we had a significance level of 0.05 and a sample size of 6, we would compare our test statistic to the value 0.7293.
Example 1: Calculating the PMCC
Calculate the Product Moment Correlation Coefficient from the following data:
[1 mark]
To do this on a scientific calculator you should go into statistics mode – there will usually be a button called MODE or MENU from where it can be accessed. This will present you with multiple options, one of which will read like a regression line (such as A+BX). Upon pressing it, you should be given a table that you can put the values in. Then, the calculator will give you key statistics from the table, including the PMCC. These can be accessed by pressing the STAT button after entering the values into the tables. Doing all of this gives:
r=0.9704
Example 2: PMCC Hypothesis Test
Are the following two variables correlated to 5\% significance?
[6 marks]
H_{0}: \rho=0, H_{1}: \rho\neq 0
Test statistic is PMCC of the variables in the table, which is r=-0.3587
Significance level: \alpha=0.05 but two tailed test so we use 0.025
Critical value from table is 0.6319>0.3587.
Do not reject H_{0}. Insufficient evidence to suggest the variables are correlated.
Product Moment Correlation Coefficient Example Questions
Question 1: Match these statements to the PMCC values.
a) Strong positive correlation.
b) Weak negative correlation.
c) No correlation.
d) Strong negative correlation.
e) Weak positive correlation.
- -0.9
- 0.3
- -0.01
- 0.875
- -0.5
[5 marks]
a) Strong positive correlation means close to 1, which corresponds to 4: 0.875
b) Weak negative correlation corresponds to a negative number that is not close to -1, which is 5: -0.5
c) No correlation means close to 0, which is 3: -0.01
d) Strong negative correlation means a number close to -1 which is 1: -0.9
e) Weak positive correlation corresponds to a positive number that is not close to 1, which is 2: 0.3
Question 2: Find the product moment correlation coefficient of the following data.
[2 marks]
To do this on a scientific calculator you should go into statistics mode – there will usually be a button called MODE or MENU from where it can be accessed. This will present you with multiple options, one of which will read like a regression line. Upon pressing it, you should be given a table that you can put the values in. Then, the calculator will give you key statistics from the table, including the PMCC. Doing all of this gives:
r=-0.3975Question 3: Tally feeds her fish varying amounts of food and monitors the amount of time they spend resting during the day. She collects 100 data points and finds a correlation of r=0.2156. She dismisses this as “clearly not correlated”. Perform a hypothesis test at the 5\% level to find if Tally should have dismissed her findings.
[3 marks]
H_{0}:\rho=0
H_{1}:\rho\neq 0
Test statistic is PMCC, which is r=0.2156.
Significance level: \alpha=0.05 but two tailed test so we use 0.025
Critical value from the table is 0.1966<0.2156
Reject H_{0}. Sufficient evidence to suggest Tally’s results are correlated.
