Revise
Non-Uniform Acceleration
Non-Uniform Acceleration Revision
Non-Uniform Acceleration
When the acceleration of a particle isn’t constant, we have to ignore the SUVAT equations. We can use calculus to relate Displacement, Velocity and Acceleration.
Make sure you are happy with the following topics before continuing.
Relationships between \textbf{s}, \textbf{v} and \textbf{a}
Think about what velocity and acceleration actually mean for a moment.
- Velocity is a change in displacement, over a period of time.
- Acceleration is a change in velocity, over a period of time.
Think back to our Displacement-Time graphs. We said that the gradient of the DT graph gives the velocity at any moment in time.
What about the Velocity-Time graphs? We said that the gradient represented the acceleration, and that the area under the graph was the distance travelled.
Well, we know how to find a gradient of a function at any point – that’s differentiation.
And we also know how to find the area under a function between two points – that’s integration.
That gives us a simple flowchart:
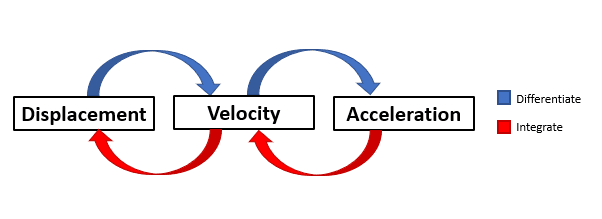
Remember, we’ve got to be careful with integration. Forgetting the + c term can throw our valuations of \textcolor{red}{v} and \textcolor{limegreen}{s} off wildly.
Finding Maxima and Minima
This calculus operates in the same way that regular calculus does.
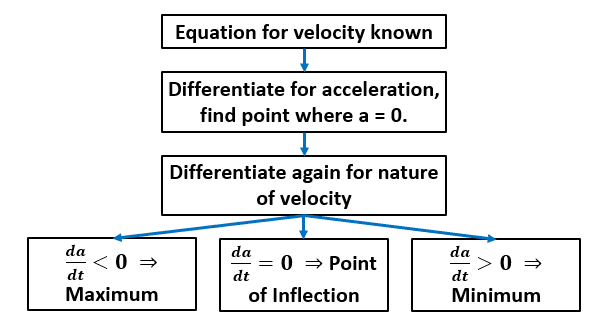
So, for example, let’s say we want to find the maximum or minimum velocity at any given point. Well, logically, we’re looking for a point in time where there’s no acceleration or deceleration. You might say, when the change in velocity, \dfrac{d\textcolor{red}{v}}{d\textcolor{purple}{t}} = 0.
Then, we’d differentiate this again to find out whether this “stationary point” is a minimum, maximum or point of inflection.
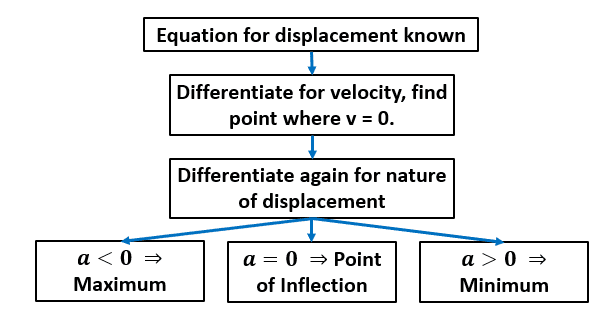
The same goes for finding a maximum or minimum displacement from a starting point, too.
We’re looking for a point where the velocity, \textcolor{red}{v} = \dfrac{d\textcolor{limegreen}{s}}{d\textcolor{purple}{t}}, is 0.
Beyond there, we’re looking to find out whether our point is a minimum, maximum or point of inflection.
So, to recap, a maximum/minimum displacement can be found when \textcolor{red}{v} = 0, and we can determine its nature by finding out the value of \textcolor{blue}{a}.
Note
The second derivative being equal to 0 does not always mean there is a point of inflection. How to handle this result is covered on the stationary points page.
Deriving the SUVAT Equations
We can use our new equations to give our SUVAT equations.
Say we have \textcolor{blue}{a} = \dfrac{d\textcolor{red}{v}}{d\textcolor{purple}{t}}
Then, \textcolor{red}{v} = \int \textcolor{blue}{a}\, d\textcolor{purple}{t} = \textcolor{blue}{a}\textcolor{purple}{t} + c
Remember, we can find c by setting \textcolor{purple}{t} = 0. Well, we label our initial velocity as u, so we can deduce that c = u, and by extension,
\textcolor{red}{v} = u + \textcolor{blue}{a}\textcolor{purple}{t}
Also, \textcolor{red}{v} = \dfrac{d\textcolor{limegreen}{s}}{d\textcolor{purple}{t}}
Then we have \textcolor{limegreen}{s} = \int \textcolor{red}{v} d\textcolor{purple}{t} = \int (u + \textcolor{blue}{a}\textcolor{purple}{t})\, d\textcolor{purple}{t} = u\textcolor{purple}{t} + \dfrac{1}{2}\textcolor{blue}{a}\textcolor{purple}{t}^2 + c
Now, we didn’t talk about what we label c when \textcolor{purple}{t} = 0. Nothing to worry about though, we’ll just call it s_0, the initial displacement point. So, we have
\textcolor{limegreen}{s} = u\textcolor{purple}{t} + \dfrac{1}{2}\textcolor{blue}{a}\textcolor{purple}{t}^2 + s_0
Example 1: Finding a Minimum or Maximum Displacement
Let’s put this into action.
Say a particle has an equation for displacement, \textcolor{limegreen}{s} = 3\textcolor{purple}{t}^3 - \textcolor{purple}{t} - 9.
Find the point where the particle is stationary, and find the nature of this stationary point.
[3 marks]
\dfrac{d\textcolor{limegreen}{s}}{dt} = \textcolor{red}{v} = 9\textcolor{purple}{t}^2 - 1 = (3\textcolor{purple}{t} + 1)(3\textcolor{purple}{t} - 1)\\
\textcolor{red}{v} = \textcolor{red}{0} when \textcolor{purple}{t} = ±\textcolor{purple}{\dfrac{1}{3}}
Of course, we can’t have a negative time, so we only have \textcolor{purple}{t} = \textcolor{purple}{\dfrac{1}{3}}.
\dfrac{d^{2}\textcolor{limegreen}{s}}{d\textcolor{purple}{t}^{2}} = \dfrac{d\textcolor{red}{v}}{d\textcolor{purple}{t}} = \textcolor{blue}{a} = 18\textcolor{purple}{t}
When \textcolor{purple}{t} = \textcolor{purple}{\dfrac{1}{3}}, \textcolor{blue}{a} = \textcolor{blue}{6}\\ 6 > 0, so we conclude that the displacement is at a minimum when \textcolor{purple}{t} = \textcolor{purple}{\dfrac{1}{3}}\text{ s}.
Example 2: Finding a Minimum or Maximum Velocity
Now, say a particle has a velocity of \textcolor{red}{v} = 25 + 8\textcolor{purple}{t} - \textcolor{purple}{t}^2.
Find the time \textcolor{purple}{t} when the particle is not accelerating or decelerating. Find out whether this point corresponds to the minimum or maximum velocity.
[3 marks]
\dfrac{d\textcolor{red}{v}}{d\textcolor{purple}{t}} = \textcolor{blue}{a} = 8 - 2\textcolor{purple}{t}
We have \textcolor{blue}{a} = \textcolor{blue}{0} when \textcolor{purple}{t} = \textcolor{purple}{4}.
\dfrac{d^{2}\textcolor{red}{v}}{d\textcolor{purple}{t}^{2}} = \dfrac{d\textcolor{blue}{a}}{d\textcolor{purple}{t}} = \textcolor{blue}{-2}
Since -2 < 0, we can conclude that we have a maximum velocity when \textcolor{purple}{t} = 4\text{ s}.
Example 3: Finding Displacement from Acceleration
A particle is accelerating at 6\textcolor{purple}{t}\text{ ms}^{-2}. Given that the initial velocity, u, is 10\text{ ms}^{-1}, and the initial displacement, s_0 is 50\text{ m}, find an equation for \textcolor{limegreen}{s} in terms of \textcolor{purple}{t}.
[4 marks]
From \textcolor{blue}{a}= 6\textcolor{purple}{t}, we have
\textcolor{red}{v} = \int \textcolor{blue}{a}\, d\textcolor{purple}{t} = \int 6\textcolor{purple}{t}\, d\textcolor{purple}{t}\\ = 3\textcolor{purple}{t}^2 + u = 3\textcolor{purple}{t}^2 + 10
By extension,
\textcolor{limegreen}{s} = \int \textcolor{red}{v}\, d\textcolor{purple}{t} = \int (3\textcolor{purple}{t}^2 + 10)\, d\textcolor{purple}{t}\\ = \textcolor{purple}{t}^3 + 10\textcolor{purple}{t} + s_0 = \textcolor{purple}{t}^3 + 10\textcolor{purple}{t} + 50
Non-Uniform Acceleration Example Questions
Question 1: For a particle with displacement s = \dfrac{1}{2}t^2 - 16\sqrt{t}, find the time t where the particle is not moving, and determine whether it is accelerating or decelerating at this point.
[3 marks]
s = \dfrac{1}{2}t^2 - 16\sqrt{t}
gives
v = \dfrac{ds}{dt} = t - \dfrac{8}{\sqrt{t}}
Then v = 0 when t = 4. Also,
a = \dfrac{dv}{dt} = \dfrac{d^{2}s}{dt^2} = 1 + \dfrac{4}{t\sqrt{t}}
Substituting t = 4, we can see that a = 1 + \dfrac{4}{8} = 1.5, so the particle is accelerating from a minimum point.
Question 2: A car is accelerating at a rate of -2t\text{ ms}^{-2}, with an initial velocity of 25\text{ ms}^{-1}. Assuming it does not start travelling backwards when its velocity is 0\text{ ms}^{-1}, how far does the car travel?
[3 marks]
a = -2t\\
gives
v = \int a\, dt = \int (-2t)\, dt = u - t^2 = 25 - t^2
meaning v = 0 when t = 5.
s = \int v\, dt = \int (25 - t^2)\, dt = 25t - \dfrac{1}{3}t^3 + c = 25t - \dfrac{1}{3}t^3
When t = 5, s = 125 - \left( \dfrac{1}{3} \times 125\right) = 83.33\text{ m (to } 2 \text{ dp)}
Question 3: A particle sets off from the origin point, and its displacement is described by s = \sin t + \cos t - 1, where t is measured in radians. Find an expression for its acceleration at time t. List all times 0 \leq t \leq 2\pi where the particle is stationary.
[4 marks]
s = \sin t + \cos t - 1
gives
v = \cos t - \sin t
and
a = - \sin t - \cos t
We know that v = 0 when \cos t = \sin t.
So we have v = 0 when \tan t = 1.
This means that the particle is stationary when t = \dfrac{\pi}{4} and \dfrac{5\pi}{4}.
