Revise
Binomial Expansion
Binomial Expansion Revision
Binomial Expansion
Binomial expansion uses binomial coefficients to expand two terms in brackets of the form (ax+b)^{n}. When n is a positive whole number the expansion is finite. When n is not, the expansion is infinite.
Pascal’s Triangle
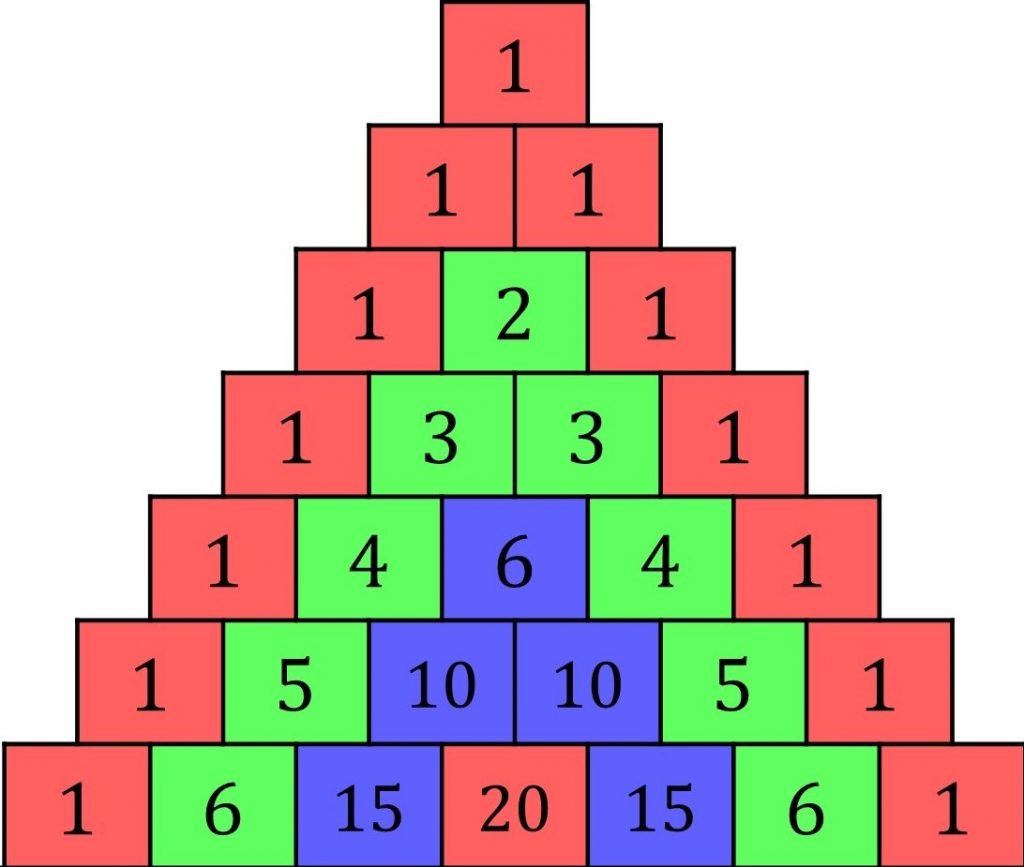
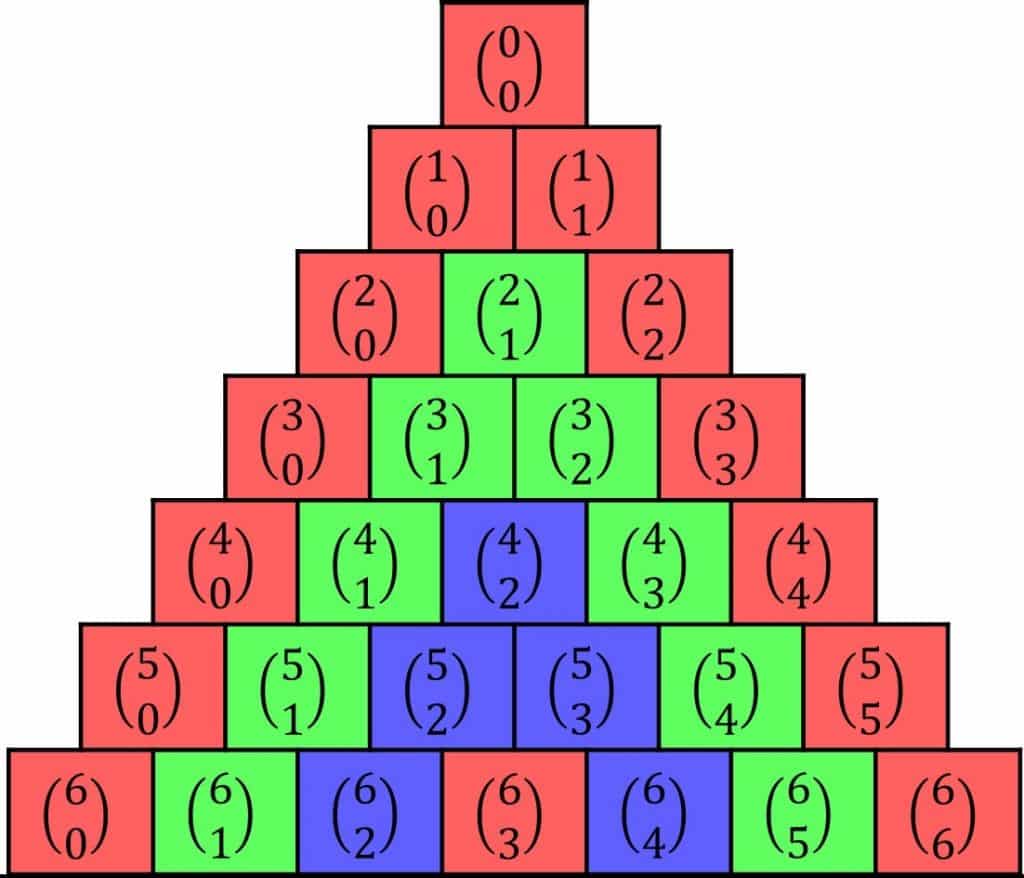
Pascal’s triangle is made by putting 1s down the sides, then every number comes from adding together the two above it.
The numbers on the nth row are the coefficients of (1+x)^{n}
(1+x)^{0}=1
(1+x)^{1}=1+x
(1+x)^{2}=1+2x+x^{2}
(1+x)^{3}=1+3x+3x^{2}+x^{3}
(1+x)^{4}=1+4x+6x^{2}+4x^{3}+x^{4}
and so on.
Binomial Coefficients
The binomial coefficient \begin{pmatrix}n\\m\end{pmatrix}=\dfrac{n!}{m!(n-m)!} where m and n are whole numbers and n>m. We can also write them as \text{}^{n}C_{m}.
The binomial coefficients are the same as the numbers in Pascal’s triangle.
This means we can write our expansion as:
(1+x)^{n}=\begin{pmatrix}n\\0\end{pmatrix}+\begin{pmatrix}n\\1\end{pmatrix}x+\begin{pmatrix}n\\2\end{pmatrix}x^{2}+...+\begin{pmatrix}n\\n-1\end{pmatrix}x^{n-1}+\begin{pmatrix}n\\n\end{pmatrix}x^{n}
General Binomial Expansion Formula
So far we have only seen how to expand (1+x)^{n}, but ideally we want a way to expand more general things, of the form (a+b)^{n}. In this expansion, the mth term has powers a^{m}b^{n-m}. We can use this, along with what we know about binomial coefficients, to give the general binomial expansion formula.
(a+b)^{n}=\begin{pmatrix}n\\0\end{pmatrix}a^{n}+\begin{pmatrix}n\\1\end{pmatrix}a^{n-1}b+\begin{pmatrix}n\\2\end{pmatrix}a^{n-2}b^{2}+...+\begin{pmatrix}n\\m\end{pmatrix}a^{m}b^{n-m}+...+\begin{pmatrix}n\\n-1\end{pmatrix}ab^{n-1}+\begin{pmatrix}n\\n\end{pmatrix}b^{n}
Example 1: Binomial Expansion
Expand (1+2x)^{2}
[2 marks]
(1+2x)^{2}=\begin{pmatrix}2\\0\end{pmatrix}1^{2}+\begin{pmatrix}2\\1\end{pmatrix}1\times2x+\begin{pmatrix}2\\2\end{pmatrix}(2x)^{2}
Find the binomial coefficients:
\begin{pmatrix}2\\0\end{pmatrix}=1
\begin{pmatrix}2\\1\end{pmatrix}=2
\begin{pmatrix}2\\2\end{pmatrix}=1
Substitute binomial coefficients into equation:
\begin{aligned}(1+2x)^{2}&=1\times1^{2}+2\times1\times2x+1\times(2x)^{2}\\[1.2em]&=1\times1+2\times2x+1\times4x^{2}\\[1.2em]&=1+4x+4x^{2}\end{aligned}
Example 2: Finding Coefficients
Find the coefficient of x^{3} in (x+8)^{6}.
[2 marks]
x^{3} term is \begin{pmatrix}6\\3\end{pmatrix}x^{3}8^{6-3}
\begin{pmatrix}6\\3\end{pmatrix}=20
8^{6-3}=8^{3}=512
x^{3} term is 512\times20x^{3}
x^{3} term is 10240x^{3}
Coefficient of x^{3} is 10240
Binomial Expansion Example Questions
Question 1: What is the eighth row of Pascal’s triangle?
(Hint: The triangle pictured on this page goes up to row seven.)
[2 marks]
1s down the sides.
1+6=7 so 7 is the next number in.
6+15=21 so 21 is the next number in.
15+20=35 so 35 is the next number in.
So the whole row is:
1,7,21,35,35,21,7,1
Question 2: Expand \left(\dfrac{1}{4}-2x\right)^{4}
[5 marks]
\begin{pmatrix}4\\0\end{pmatrix}=1
\begin{pmatrix}4\\1\end{pmatrix}=4
\begin{pmatrix}4\\2\end{pmatrix}=6
\begin{pmatrix}4\\3\end{pmatrix}=4
\begin{pmatrix}4\\1\end{pmatrix}=1
\left(\dfrac{1}{4}-2x\right)^{4}=\big( 1\times(-2x)^{4}\big) +\big( 4\times\dfrac{1}{4}(-2x)^{3}\big) +\big( 6\times\left(\dfrac{1}{4}\right)^{2}(-2x)^{2}\big) +\big( 4\times\left(\dfrac{1}{4}\right)^{3}(-2x)\big) +\big( 1\times\left(\dfrac{1}{4}\right)^{4}\big)
\left(\dfrac{1}{4}-2x\right)^{4}=\big( 1\times16x^{4}\big) +\big( 4\times\dfrac{1}{4}\times(-8)x^{3}\big) +\big( 6\times\dfrac{1}{16}\times4x^{2}\big) +\big( 4\times\dfrac{1}{64}\times(-2)x\big) +\big( 1\times\dfrac{1}{256}\big)
\left(\dfrac{1}{4}-2x\right)^{4}=16x^{4}-8x^{3}+\dfrac{24}{16}x^{2}-\dfrac{8}{64}x+\dfrac{1}{256}
\left(\dfrac{1}{4}-2x\right)^{4}=16x^{4}-8x^{3}+\dfrac{3}{2}x^{2}-\dfrac{1}{8}x+\dfrac{1}{256}
Question 3: What is the coefficient of x^{4} in (5x-2)^{9}?
[3 marks]
x^{4} term is \begin{pmatrix}9\\4\end{pmatrix}(5x)^{4}(-2)^{5}=-\begin{pmatrix}9\\4\end{pmatrix}5^{4}x^{4}2^{5}
\begin{pmatrix}9\\4\end{pmatrix}=126
5^{4}=625
2^{5}=32
x^{3} coefficient is -126\times625\times32=-2520000
Question 4: Find p such that the x^{2} coefficient in \left(\dfrac{2}{3}x+p\right)^{3} is 4.
[3 marks]
x^{2} coefficient is \begin{pmatrix}3\\2\end{pmatrix}\left(\dfrac{2}{3}\right)^{2}p
\begin{pmatrix}3\\2\end{pmatrix}=3
\left(\dfrac{2}{3}\right)^{2}=\dfrac{4}{9}
Hence, 3\times\dfrac{4}{9}\times p=4
\dfrac{4}{3}p=4
p=4\times\dfrac{3}{4}
p=3
Binomial Expansion Worksheet and Example Questions
Polynomials
A Level
