pH Calulations
pH Calulations Revision
\text{pH} Calculations
\text{pH} is a number that represents the acidity or basicity of an aqueous solution. It is a measure of the concentration of \text{H}^+ ions contained in a solution. \text{pH} is measured on a log scale.
Brønsted Lowry Acids and Bases
- A Brønsted Lowry Acid is a substance that donates protons.
- A Brønsted Lowry Base is a substance that accepts protons.
In the reaction below, the hydrochloric acid acts as an acid as it can donate a proton while the ammonia acts as a base as it can accept protons.
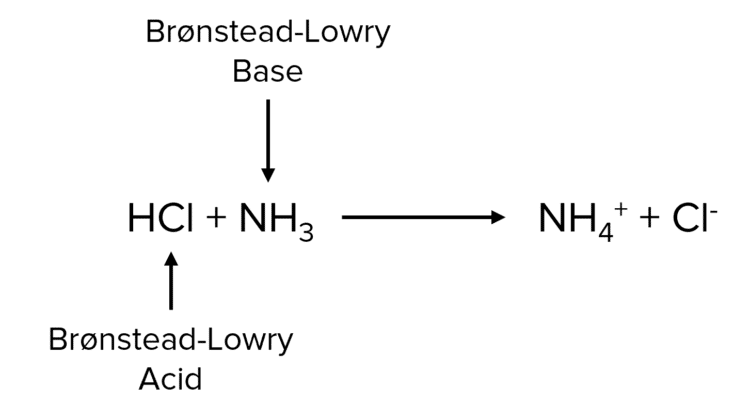
The Brønsted Lowry acid is linked to a conjugate base on the other side of the equation, they are known as a conjugate pair. The conjugate base will likely be a negative ion, capable of accepting a \text{H}+ ion to reform the acid. Similarly, a Brønsted Lowry base is linked to a conjugate acid on the other side of the equation. The conjugate acid will be a positive ion, capable of donating a \text{H}^+ ion to reform the base.
A quick way to identify the conjugate of a substance is that there should be a difference of a proton between them.
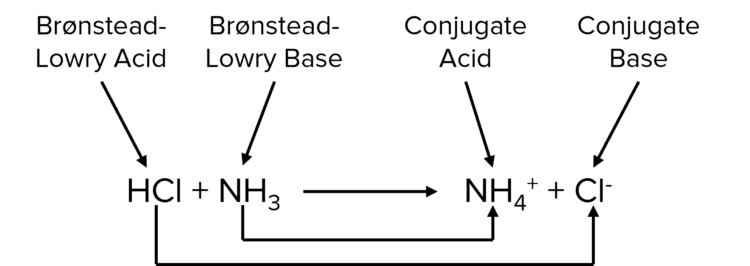
In the reaction there is a 1 proton difference between \text{HCl} and \text{Cl}^- so \text{Cl}^- must be the conjugate base. There is also a one proton difference between \text{NH}_3 and \text{NH}_4^+ so \text{NH}_4^+ must be the conjugate acid.
\text{pH} of Strong Acids
Strong acids are acids that completely dissociate in solution.
\text{HX}_{\text{(s)}}\rarr\text{H}^+_{\text{(aq)}}+\text{X}^-_{\text{(aq)}}
As the acid totally dissociates, the \text{pH} of the acid can be calculated directly from the concentration of \text{H}^+ ions. This is done by taking the negative log of the concentration:
\text{pH}=-\text{log}\left[\text{H}^+\right]
When the \text{pH} is known, the concentration of \text{H}^+ ions can be found by following the inverse process:
\left[\text{H}^+\right]=10^{-\text{pH}}
For monoprotic (i.e. acids that only donate one hydrogen ion, such as \text{HCl} or \text{HNO}_3 the concentration of hydrogen ions is the same as the concentration of the acid. For diprotic acids (those that donate two hydrogen ions, such as \text{H}_2\text{SO}_4), the concentration of \text{H}^+ is double that of the acid.
The Ionic Product of Water, Kw
In aqueous solutions, and pure water, \text{H}_2\text{O} will dissociate in the equilibrium below:
\text{H}_2\text{O}_{\text{(l)}}\rightleftharpoons\text{H}^+_{\text{(aq)}}+\text{OH}^-_{\text{(aq)}}
Using the \text{K}_c equation we can create an expression for the equilibrium:
\text{K}_c=\frac{\left[\text{H}^+\right]\left[\text{OH}^-\right]}{\left[\text{H}_2\text{O}\right]}
This can then be rearranged to obtain an expression for the ionic product of water \text{K}_w.
\left[\text{H}^+\right]\left[\text{OH}^-\right]=\text{K}_c\left[\text{H}_2\text{O}\right]=\text{K}_w
\text{K}_c is typically a very small number (almost negligible), while \left[\text{H}_2\text{O}\right] is constant, making \text{K}_w effectively constant. In pure water and neutral solutions \left[\text{H}^+\right] = \left[\text{OH}^-\right] . So the equation can be re-written as
\text{K}_w=\left(\left[\text{H}^+\right]\right)^2
The \text{K}_w value of an aqueous solution at room temperature \left(25\degree \text{C}\right) is 1.0\times10^{-14}\text{ mol}^2\text{ dm}^{-6}.
The ionic product of water can be used to calculate the \text{pH} of a strong base. Strong bases completely dissociate into their ions in solution.
\text{BX}_{\text{(s)}}\rarr\text{B}^-_{\text{(aq)}}+\text{X}^+_{\text{(aq)}}
To calculate the pH of a strong base, we need to use the pH equation as well as the equation for the ionic product of water. This is done by first calculating the value of \left[\text{H}^+\right] by taking the square root of \text{K}_w. This can then be fed into the \text{pH} equation:
\text{pH of a Base}=-\text{log } \sqrt{\text{K}_w}
pH of Weak Acids
Weak acids are ones that only partially dissociate into solution:
\text{HA}_{\text{(s)}}\rightleftharpoons\text{H}^+ + \text{A}^-
This equilibrium can be studied using the acid dissociation constant \text{K}_a. Larger values of \text{K}_a will correspond to compounds that dissociate more completely into solution, and therefore to stronger acids. \text{K}_a is calculated in the same manner as all other equilibrium constants:
\text{K}_a=\frac{\left[\text{H}^+\right]\left[\text{A}^-\right]}{\left[\text{HA}\right]}
This allows the calculation of \left[\text{H}^+\right] and therefore for the \text{pH} of a weak acid. When using \text{K}_a to calculate the pH of weak acids, two key assumptions are made.
- That \left[\text{H}^+\right]=\left[\text{A}^-\right] because monoprotic acids dissociate into a 1:1 ratio of \text{H}^+ ions and conjugate base (A).
- That the concentration of the acid (HA) at equilibrium is the same as the initial concentration of the acid. This is because there is only a small dissociation of the acid and so the actual value of \left[\text{HA}\right] will only be negligibly different from the initial concentration.
These assumptions mean that the Ka expression can be simplified to
\text{K}_a=\frac{\left(\left[\text{H}^+\right]\right)^2}{\left[\text{HA}\right]_{\text{Initial}}}
It is very common that the \text{pK}_a of a substance is given as opposed to its \text{K}_a. \text{pK}_a is the negative logarithm of \text{K}_a, it also represents the strength of an acid. To convert \text{pK}_a to \text{K}_a the following equation can is used:
\text{K}_a=10^{-\text{pK}_a}
Example 1: Calculating the \text{pH} of a strong base
Calculate the \text{pH} of a \textcolor{#00bfa8}{0.15\text{ mol dm}^{-3}} sample of \text{NaOH}. The ionic product of water, \text{K}_w at 25\degree \text{C} is \textcolor{#f21cc2}{1.0\times10^{-14}\text{ mol}^2\text{ dm}^{-6}}.
[3 marks]
Step 1: Calculate the the concentration of \left[\text{H}^+\right].
\begin{aligned}\text{K}_w&=\left[\text{H}^+\right]\left[\text{OH}^-\right]\\\left[\text{H}^+\right]&=\frac{\text{K}_w}{\left[\text{OH}^-\right]}\\ &=\frac{\textcolor{#f21cc2}{10^{-14}}}{\textcolor{#00bfa8}{0.15}}\\ &=\textcolor{#008d65}{6.67\times10^{-14}\text{ mol dm}^{-3}}\end{aligned}
Step 2: Calculate the \text{pH}.
\begin{aligned}\text{pH}&=-\text{log } 6.67\times10^{-14}\\ &=\textcolor{#008d65}{13.2}\end{aligned}
Example 2: Calculating the \text{pH} of a Weak Acid
Propanoic Acid will partially dissociate in water:
\text{CH}_3\text{CH}_2\text{COOH}\rightleftharpoons\text{CH}_3\text{CH}_2\text{COO}^- + \text{H}^+
Calculate the \text{pH} of a solution of propanoic acid with a concentration of \textcolor{#00bfa8}{0.04\text{ mol dm}^{-3}}. The \text{K}_a is \textcolor{#f21cc2}{1.34\times10^{-5}\text{ mol dm}^{-3}}.
[3 marks]
Step 1: Calculate the value of \left[\text{H}^+\right].
\begin{aligned}\text{K}_a&=\frac{\left(\left[\text{H}^+\right]\right)^2}{\left[\text{CH}_3\text{CH}_2\text{COOH}\right]}\\\left[\text{H}^+\right]&=\sqrt{\text{K}_a\left[\text{CH}_3\text{CH}_2\text{COOH}\right]}\\ &=\sqrt{\textcolor{#f21cc2}{1.34\times10^{-5}}\times\textcolor{#00bfa8}{0.04}}\\ &=\textcolor{#008d65}{7.32\times10^{-4}\text{ mol dm}^{-3}}\end{aligned}
Step 2: Calculate the \text{pH}.
\begin{aligned}\text{pH}=-\text{log }7.32\times10^{-4}=\textcolor{#008d65}{3.1}\end{aligned}
pH Calulations Example Questions
Question 1: Give the mathematical definitions the following terms:
- \text{K}_w
- \text{pH}
[2 marks]
a. \text{K}_w = \left[\text{OH}^-\right]\left[\text{H}^+\right]
b. \text{pH} = -\text{log } \left[\text{H}^+\right]
Question 2: Calculate the \text{pH} at 25\degree \text{C} of 2.50\text{ mol dm}^{-3} of \text{NaOH}.
[3 marks]
\begin{aligned}\left[\text{H}^+\right]&=\frac{10^{-14}}{2.50}\\ &=4.0\times10^{-15}\text{ mol dm}^{-3}\end{aligned}
\text{pH}=-\text{log }4.0\times10^{-15}=14.4
(One mark per correct line of working.)
Question 3: Explain the term Brønsted Lowry Base and write an equation for the reaction of methylamine \left(\text{CH}_3\text{NH}_2\right) with water to produce an alkaline solution.
[2 marks]
A Brønsted Lowry base is a proton acceptor (/ \text{H}^+ acceptor).
\text{CH}_3\text{NH}_3 + \text{H}_2\text{O}\rightleftharpoons\text{CH}_3\text{NH}_4^+ +\text{OH}^-Question 4: A solution of ethanoic acid has a \text{pH} of 3.2 at 25\degree \text{C}. Given that the \text{K}_a for ethanoic acid is 1.70\times10^{-5}\text{ mol dm}^{-3}.
Calculate the concentration of the acid.
[4 marks]
Step 1: Calculate the value of \left[\text{H}^+\right].
\left[\text{H}^+\right]=10^{-\text{pH}}=6.31\times10^{-4}\text{ mol dm}^{-3}
Step 2: Calculate the value of \left[\text{CH}_3\text{COOH}\right].
\begin{aligned}\text{K}_a&=\frac{\left(\left[\text{H}^+\right]\right)^2}{\text{CH}_3\text{COOH}}\\\left[\text{CH}_3\text{COOH}\right]&=\frac{\left(\left[\text{H}^+\right]\right)^2}{\text{K}_a}\\ &=0.023\text{ mol dm}^{-3}\end{aligned}
(One mark for step 1. Three marks for step 2, one mark per correct line of calculation.)
You May Also Like...

MME Learning Portal
Online exams, practice questions and revision videos for every GCSE level 9-1 topic! No fees, no trial period, just totally free access to the UK’s best GCSE maths revision platform.