Calculating the Equilibrium Constant (Kc)
Calculating the Equilibrium Constant (Kc) Revision
Calculating the Equilibrium Constant \left(\text{Kc}\right)
The equilibrium constant is a ratio that shows the relation between the concentration of products to the concentration of reactants.
The Equilibrium Constant, \left(\text{Kc}\right)
For a reversible reaction, the equilibrium constant shows the position of the equilibrium for a reaction at a given temperature. To find the equilibrium constant, we divide the concentrations of the products by the concentration of the reactants.
\text{aW}+\text{bX}\rightleftharpoons\text{cY}+\text{dZ}
\text{Kc}= \dfrac{\text{[Y]}^{\text{c}}\text{[Z]}^{\text{d}}}{\text{[W]}^{\text{a}}\text{[X]}^{\text{b}}}
Example: \text{N}_{2\left(\text{g}\right)}+3\text{H}_{2\left(\text{g}\right)}\rightleftharpoons2\text{NH}_{3\left(\text{g}\right)}
\text{Kc}= \dfrac{\text{[NH}_3\text{]}^2}{\text{[N}_2\text{]}\text{[H}_2\text{]}^3}
The higher the value of \text{K}_{\text{c}}, the further to the right (i.e. towards the products) the equilibrium will lie. The lower the value, the further to the left.
Effect of Changing Conditions on \left(\text{Kc}\right)
\text{K}_c values correlate with the amount of products. If \text{K}_c values are bigger, there will be a larger amount of products. If \text{K}_c is smaller, there will be a smaller amount of products, meaning the equilibrium favours the reactants.
The only condition that affects \text{K}_c is temperature. Changing the pressure, concentration or adding a catalyst would have no effect on the \text{K}_c value and it would remain constant.
Effect of Changing Temperature on Kc
The direction that the equilibrium will shift, is dependent on the nature of the reaction. If the forward reaction is exothermic, then an increase in temperature would lead to a decrease in products/ yield as the equilibrium would shift towards the reactants to oppose the increase in the temperature.
If there is a change in temperature, and the equilibrium shifts to the left, then the \text{K}_c value will decrease. Similarly, if the equilibrium shifts to the right after a change in the temperature, the \text{K}_c value will increase.
Example 1: Calculating a \text{Kc} Value
Answering \text{Kc} questions can involve a lot of steps but the example below shows, in detail, how a standard question is usually answered.
A flask containing a mixture of \textcolor{#00bfa8}{0.250\text{ mol}} of ethanoic acid and \textcolor{#f21cc2}{0.160\text{ mol}} of ethanol was maintained at 25\degree\text{C} until the following equilibrium was established.
[8 marks]
\text{CH}_3\text{COOH}_{\text{(l)}} + \text{C}_2\text{H}_5\text{OH}_{\left(\text{l}\right)} \rightleftharpoons \text{CH}_3\text{COOC}_2\text{H}_{5\left(\text{l}\right)} + \text{H}_2\text{O}_{\left(\text{l}\right)}
The ethanoic acid present at equilibrium required \textcolor{#a233ff}{72.5\text{ cm}^3} of a \textcolor{#eb6517}{1.50\text{ mol dm}^{-3}} solution of sodium hydroxide for complete reaction.
Calculate the value of the equilibrium constant, \text{Kc}, for this reaction at 25\degree\text{C}.
- Firstly, create a table that looks like this.
| \text{CH}_3\text{COOH} | \text{C}_2\text{H}_5\text{OH} | \text{CH}_3\text{COOC}_2\text{H}_5 | \text{H}_2\text{O} | |
| Initial Moles | ||||
| Equilibrium Moles |
On the far left column, always put in initial moles, equilibrium moles and concentration. At the top of the table put in each of the reactants and products. Include stoichiometric coefficients as well.
- Next, fill in all the known information given in the question. We were given the moles of ethanoic acid and the moles of ethanol.
| \text{CH}_3\text{COOH} | \text{C}_2\text{H}_5\text{OH} | \text{CH}_3\text{COOC}_2\text{H}_5 | \text{H}_2\text{O} | |
| Initial Moles | \textcolor{#00bfa8}{0.250} | \textcolor{#f21cc2}{0.160} | ||
| Equilibrium Moles |
- The initial moles of the products is always 0 (unless stated otherwise). So we can also input that into the table.
| \text{CH}_3\text{COOH} | \text{C}_2\text{H}_5\text{OH} | \text{CH}_3\text{COOC}_2\text{H}_5 | \text{H}_2\text{O} | |
| Initial Moles | \textcolor{#00bfa8}{0.250} | \textcolor{#f21cc2}{0.160} | 0 | 0 |
| Equilibrium Moles |
- We were given the information about the amount and concentration of \text{NaOH} that was used to neutralise the ethanoic acid at equilibrium. So we can use that information to find the moles of ethanoic acid at equilibrium.
\text{Moles of NaOH}=\text{c}\times\text{v}=\textcolor{#eb6517}{1.5}\times\dfrac{\textcolor{#a233ff}{72.5}}{1000}=\textcolor{#008d65}{0.10875}
\text{NaOH}+\text{CH}_3\text{COOH}\rightarrow\text{CH}_3\text{COO}^-\text{Na}^++\text{H}_2\text{O}
\text{Ratio of NaOH} to \text{CH}_3\text{COOH}= 1:1
\text{Moles of CH}_3\text{COOH} = \textcolor{#008d65}{0.10875}
We can put that into the table.
| \text{CH}_3\text{COOH} | \text{C}_2\text{H}_5\text{OH} | \text{CH}_3\text{COOC}_2\text{H}_5 | \text{H}_2\text{O} | |
| Initial Moles | \textcolor{#00bfa8}{0.250} | \textcolor{#f21cc2}{0.160} | 0 | 0 |
| Equilibrium Moles | \textcolor{#008d65}{0.10875} |
-
Using the moles of ethanoic acid at equilibrium, we can work out the moles of other substances at equilibrium.
Since we know the moles of ethanoic acid that remain, we can also calculate how much had reacted.
\text{Moles of ethanoic acid reacted}=\textcolor{#00bfa8}{0.250}-0.10875=\textcolor{#008d65}{0.14125}
The moles of \text{CH}_3\text{COOC}_2\text{H}_5 and \text{H}_2\text{O} at equilibrium will be the same as the moles of ethanoic acid that reacted. This is due to the 1:1 ratio of the stoichiometric coefficients.
| \text{CH}_3\text{COOH} | \text{C}_2\text{H}_5\text{OH} | \text{CH}_3\text{COOC}_2\text{H}_5 | \text{H}_2\text{O} | |
| Initial Moles | \textcolor{#00bfa8}{0.250} | \textcolor{#f21cc2}{0.160} | 0 | 0 |
| Equilibrium Moles | \textcolor{#008d65}{0.10875} | \textcolor{#008d65}{0.14125} | 0.14125 |
- The moles of ethanoic acid reacted will be the same as the moles of ethanol reacted due to the 1:1 ratio.
So the equilibrium moles of ethanol will be \textcolor{#f21cc2}{0.160} - 0.14125 = \textcolor{#008d65}{0.01875\text{ mol}}
| \text{CH}_3\text{COOH} | \text{C}_2\text{H}_5\text{OH} | \text{CH}_3\text{COOC}_2\text{H}_5 | \text{H}_2\text{O} | |
| Initial Moles | \textcolor{#00bfa8}{0.250} | \textcolor{#f21cc2}{0.160} | 0 | 0 |
| Equilibrium Moles | \textcolor{#008d65}{0.10875} | \textcolor{#008d65}{0.01875} | \textcolor{#008d65}{0.14125} | 0.14125 |
- Usually, we would now calculate concentration. But the \text{Kc} equation would be
\text{Kc}=\dfrac{\text{[CH}_3\text{COOC}_2\text{H}_5\text{]}\text{[H}_2\text{O]}}{\text{[CH}_3\text{COOH] [C}_2\text{H}_5\text{OH]}}
So, the volumes would cancel out since they would all be the same. This means, we can just use moles to work out \text{Kc}.
\text{Kc}=\dfrac{0.14125\times0.14125}{0.10875\times0.01875}=\textcolor{#008d65}{9.78}
Example 2: Deducing the Units of \text{K}_{\text{c}}
\text{PCl}_{3\left(\text{g}\right)}+\text{Cl}_{2\left(\text{g}\right)}\rightleftharpoons\text{PCl}_{5\left(\text{g}\right)}
Work out the units for the \text{Kc} of this reaction:
[4 marks]
\text{Kc}= \dfrac{\text{[PCl}_5\text{]}}{\text{[PCl}_3\text{]}\text{[Cl}_2\text{]}}
The unit for concentration is \text{mol dm}^{-3}. We can use this to calculate the units for \text{Kc}.
\text{Kc units}= \dfrac{\left(\text{mol dm}^{-3}\right)}{\left(\text{mol dm}^{-3}\right)\left(\text{mol dm}^{-3}\right)}
We can cancel down the units.
\text{Kc units} = \dfrac{1}{\left(\text{mol dm}^{-3}\right)}
Which can also be written as
\text{Kc units} =\text{mol}^{-1}\text{dm}^3
Note: It is possible for there to be no units for a \text{Kc} value. This happens if all of the concentration units cancel out.
Example 3: Calculating Equilibrium Moles using \text{K}_\text{c}
The following equilibrium is established:
\text{H}_{2 (g)}+\text{I}_{2 (g)}\rightleftharpoons2\text{HI}
To reach this equilibrium \textcolor{#00bfa8}{0.300\text{ mol}} of \text{H}_2 was mixed with \textcolor{#f21cc2}{0.300\text{ mol}} of \text{I}_2. The \text{K}_c of this equilibrium is \textcolor{#a233ff}{0.330}. Calculate the equilibrium moles of each substance.
[6 marks]
Step 1: Create a table of the initial and equilibrium moles.
| \text{H}_2 | \text{I}_2 | 2\text{HI} | |
| Initial Moles | \textcolor{#00bfa8}{0.300} | \textcolor{#f21cc2}{0.300} | 0 |
| Equilibrium Moles | 0.300-x | 0.300-x | 2x |
Step 2: Calculate the Value of X.
\begin{aligned}\textcolor{#a233ff}{0.330}&=\frac{(2x)^2}{(\textcolor{#00bfa8}{0.300}-x)(\textcolor{#f21cc2}{0.300}-x)}\\\textcolor{#a233ff}{0.330}&=\frac{(2x)^2}{(0.300-x)^2}\\\sqrt{\textcolor{#a233ff}{0.330}}&=\frac{2x}{0.300-x}\\0.5475(0.300-x) &=2x\\0.1723-0.5745x &=2x\\2x+0.5475x &=0.1723\\2.5745x &=0.1732\\x &=\textcolor{#008d65}{0.0669}\end{aligned}
Step 3: Calculate the equilibrium moles of each substance.
\begin{aligned}\text{Moles of HI at eqm}=2x=&\textcolor{#008d65}{0.1339\text{ mol}}\\\text{Moles of I}_2\text{ at eqm}= 0.300-x=&\textcolor{#008d65}{0.2331\text{ mol}}\\\text{Moles of H}_2\text{ at eqm}= 0.300-x=&\textcolor{#008d65}{0.2331\text{ mol}}\end{aligned}
Calculating the Equilibrium Constant (Kc) Example Questions
Question 1: A possible first step when manufacturing nitric acid is to form nitrogen monoxide from nitrogen and oxygen in a reversible reaction.
Write an equation for this reaction and deduce an expression for the equilibrium constant.
[2 marks]
\text{N}_2+\text{O}_2\rightleftharpoons2\text{NO}
\text{Kc}=\dfrac{\text{[NO]}^2}{\text{[N}_2\text{] [O}_2\text{]}}
Question 2: Nitrogen dioxide dissociates according to the equation below.
2\text{NO}_{2\left(\text{g}\right)}\leftrightarrows2\text{NO}_{\left(\text{g}\right)}+\text{O}_{2\left(\text{g}\right)}
When 23.8\text{ g} of nitrogen dioxide were heated to a constant temperature, \text{T}, in a flask of volume 12.5\text{ dm}^3, an equilibrium mixture was formed which contained 7.85\text{ g} of oxygen.
Write an expression for the equilibrium constant \text{Kc}, then calculate the value of this constant at temperature \text{T} and give its units.
[7 marks]
\text{Kc}=\dfrac{\text{[NO]}^2\text{[O}_2\text{]}}{\text{[NO}_2\text{]}^2}
\begin{aligned}\text{Moles of O}_2\text{ at equilibrium}&=\frac{\text{Mass}}{\text{M}_r}\\\text{}\\ &= \dfrac{7.85}{32}\\\text{}\\ &=0.24531\end{aligned}
\text{Moles of NO at equilibrium}= 2\times0.24531=0.49063
\begin{aligned}\text{Moles of NO}_2\text{ at equilibrium}&=\frac{\text{Mass}}{\text{M}_r}\\\text{}\\&=\dfrac{23.8}{46}-0.49063\\\text{}\\&=0.026761\end{aligned}
\text{Kc}=\dfrac{\left(\dfrac{0.49063}{12.5}\right)^2\left(\dfrac{0.24531}{12.5}\right)}{\left(\dfrac{0.026761}{12.5}\right)^2}
\text{Kc}=6.60
\text{Units}=\text{ mol dm}^{-3}
Question 3: below is a graph showing the change in \text{K}_c with temperature for an equilibrium system.
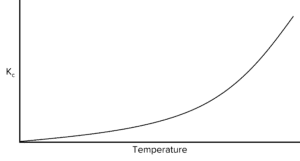
Using the graph, deduce whether the reaction is exothermic or endothermic.
[2 marks]
As temperature increases, Kc also increases . So the reaction is endothermic.
You May Also Like...

MME Learning Portal
Online exams, practice questions and revision videos for every GCSE level 9-1 topic! No fees, no trial period, just totally free access to the UK’s best GCSE maths revision platform.