Errors and Uncertainties
Errors and Uncertainties Revision
Uncertainty
Every time you make a measurement, there will always be some uncertainty. This means that we cannot ever measure the exact true value of a quantity. You could make the exact same measurement again and get a slightly different answer due to random error. We can calculate this uncertainty.
Calculating Uncertainties
We can calculate the uncertainty of a mean from a set of results. If you have a set of results that vary quite a lot between each repeat then your uncertainty will be larger. This is because your results will not be precise. On the other hand, if your results are very consistent for each repeat, then your uncertainty will be smaller.
The equation to calculate the uncertainty is:
\text{Uncertainty} = \dfrac{\text{Range}}{2}
We represent the uncertainty by writing the mean, followed by a “\pm” and then the uncertainty. For example, 5.06 \pm 0.05 \: \text{m} etc.
Errors
Errors in experiments increase uncertainty in measured values.
There are two main types of error:
- Random Error – this is when measured values vary randomly around the true value. Random error is very common in experiments due to human error and random variations. By taking many measurements and calculating the mean, we can overcome the issue of random errors.
- Systematic Error – this is when an issue in experimental design or equipment causes the measured value to be consistently too high or consistently too low. These errors are harder to identify.
Accuracy and Precision
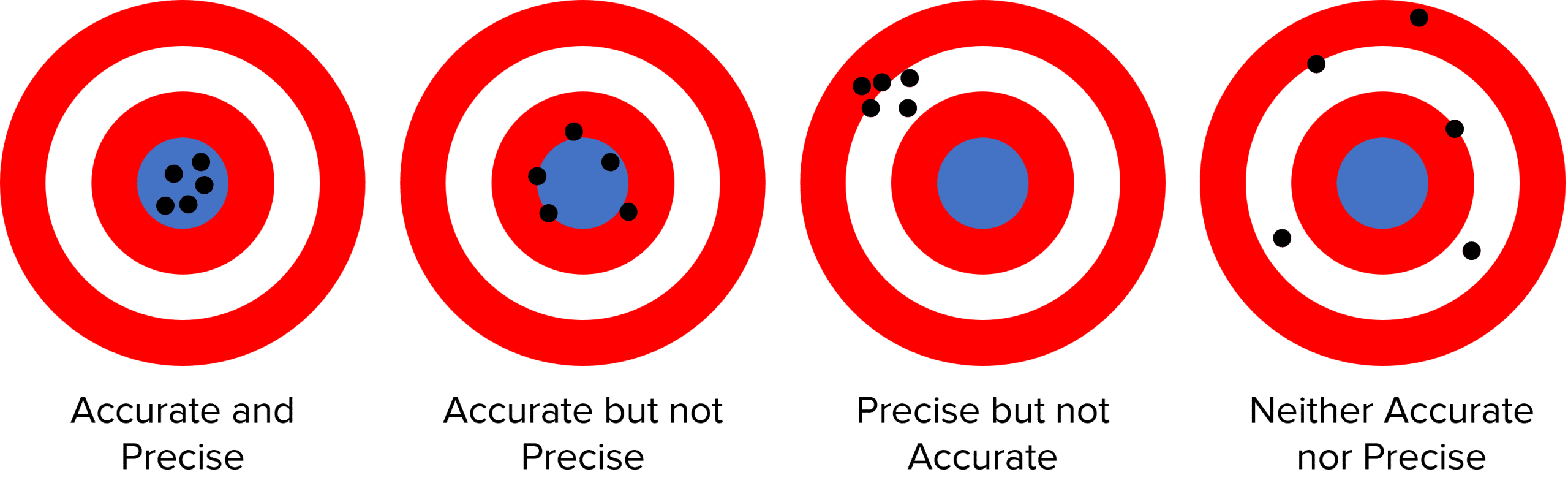
When we take measurements we want to be both accurate and precise.
- Accuracy is when the measurements are close to the correct value.
- Precision is when the measurements are close together.
If we imagine the centre of the following targets is the true value we are trying to measure, the diagrams below show the difference between accuracy and precision.
Example: Calculating Uncertainties
Lets calculate the uncertainty from a set of results:
| Repeat 1 | Repeat 2 | Repeat 3 | Repeat 4 | Mean | |
| Force applied \left(\text{N}\right) | 5.1 | 4.8 | 4.6 | 4.7 | 4.8 |
First we must work out the range of the results. This is just the largest number take away the smallest number.
\text{Range} = 5.1 - 4.6 = 0.5
Then we use this to calculate the uncertainty:
\begin{aligned} \text{Uncertainty} &= \dfrac{\text{Range}}{2} \\ \\ \text{Uncertainty} &= \dfrac{0.5}{2} = 0.25 \end{aligned}So our uncertainty in the mean is 0.25 \: \text{N}.
We can write our mean as 4.8 \pm 0.25 \: \text{N}.
Errors and Uncertainties Example Questions
Question 1: Calculate the uncertainty in the mean of the following results.
| Repeat \boldsymbol{1} | Repeat \boldsymbol{2} | Repeat \boldsymbol{3} | Mean | |
| Rate of Reaction \left(\textbf{s}^{-1}\right) | 10.4 | 12.1 | 12.2 | 11.6 |
[2 marks]
\text{Mean} =\boldsymbol{11.6 \pm 0.9} \: \textbf{s}^{-1}
Question 2: Calculate the uncertainty in the mean of the following results.
| Repeat \boldsymbol{1} | Repeat \boldsymbol{2} | Repeat \boldsymbol{3} | Mean | |
| Velocity \left(\textbf{m/s}\right) | 47 | 44 | 48 | 46.3 |
[2 marks]
\text{Mean} =\boldsymbol{46.3 \pm 2} \: \textbf{m/s}
Question 3: Below are two different students’ results tables of an experiment:
Student A
| Repeat \boldsymbol{1} | Repeat \boldsymbol{2} | Repeat \boldsymbol{3} | Mean | |
| Temperature \left(\degree \textbf{C}\right) | 101 | 85 | 102 | 96 |
Student B
| Repeat \boldsymbol{1} | Repeat \boldsymbol{2} | Repeat \boldsymbol{3} | Mean | |
| Temperature \left(\boldsymbol{\degree} \textbf{C}\right) | 100 | 100 | 99 | 100 |
a) Without making any calculations, state which student’s results will have a bigger uncertainty. Give a reason for your answer.
[2 marks]
b) Calculate the uncertainty of each set of results.
[3 marks]
a) Student A.
The results vary more, therefore there will be a bigger uncertainty.
b)
Student A:
\text{Uncertainty} = \dfrac{\text{Range}}{2} = \dfrac{102-85}{2} = \boldsymbol{8.5}\text{Mean} = \boldsymbol{96 \pm 8.5 \degree} \textbf{C}
Student B:
\text{Uncertainty} = \dfrac{\text{Range}}{2} = \dfrac{100-99}{2} = \boldsymbol{0.5}\text{Mean} = \boldsymbol{99.7 \pm 0.5 \degree} \textbf{C}
Question 4: Explain the difference between accuracy and precision.
[2 marks]
Accuracy is when the measurements are close to the correct value.
Precision is when the measurements are close together.