Radioactive Half-life
Radioactive Half-life Revision
Radioactive Half-life
Because radioactive decay is random, you cannot predict when a single nucleus will decay. However, you can predict how long it will take for half of the nuclei in a sample to decay. This is called the half-life of the sample.
Calculating Half-life
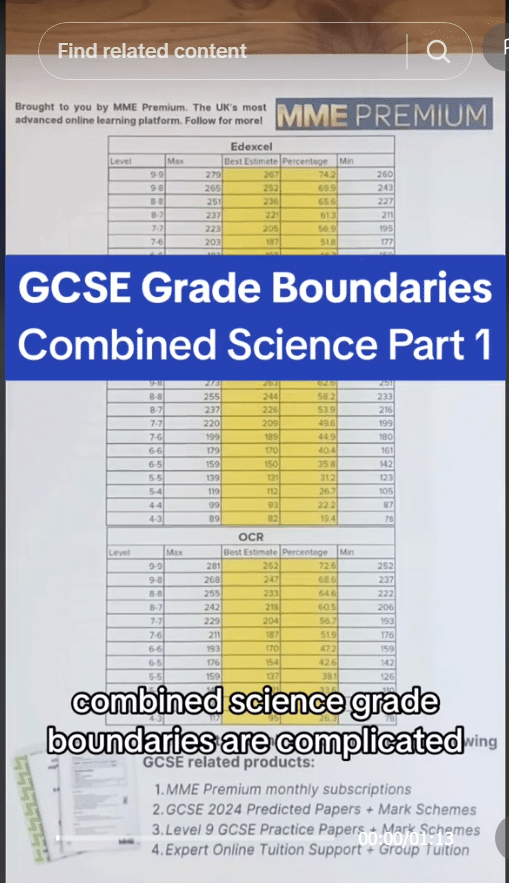
The definition of half-life is the time taken for the count rate from a sample to decrease to half the initial value. If we use a radiation detector, such as a Geiger-Muller tube, we can measure the radiation being emitted from a a sample and calculate the radioactive half life from the results.
First, you need to plot a graph of the counts per minute against the time. Then, extrapolate the time taken for the counts to reduce by a half. In this example, the original counts was measured to be 300 \text{ counts per minute} and so half the counts is 150 \text{ counts per minute}. You can see from the graph that this corresponds to 9 \text{ days}. Therefore the half-life of this sample is 9\text{ days}.
Calculations Using Half-Life
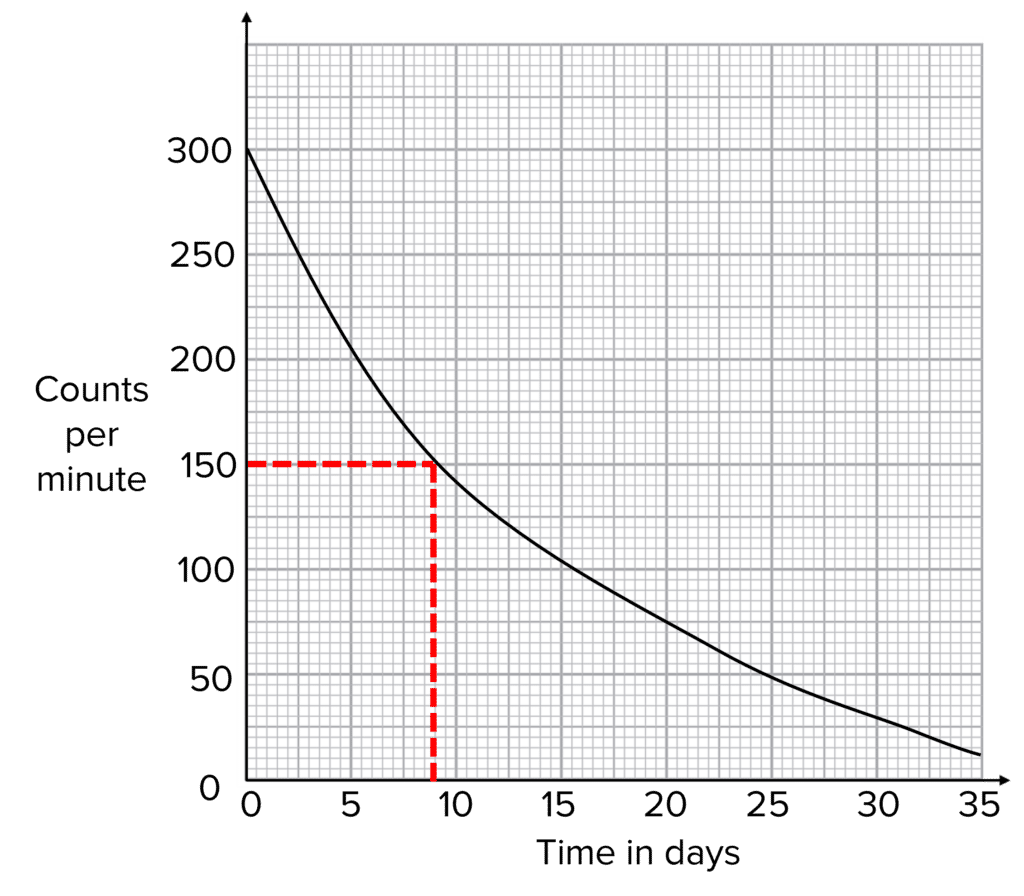
If we know the half-life of a sample we can determine how much smaller the count rate will be after a given number of half-lives.
For example, after 2\text{ half-lives}, the radioactivity of a sample will be \dfrac{1}{2}\times \dfrac{1}{2} = \bold{\color{f21cc2}{\dfrac{1}{4}}} of the original radioactivity. This is the same as saying it is 4 times smaller.
After 3\text{ half-lives}, the radioactivity will be \dfrac{1}{2} \times \dfrac{1}{2} \times \dfrac{1}{2} = \bold{\color{f21cc2}{\dfrac{1}{8}}} of the original activity, or 8 times smaller.
Radioactive Half-life Example Questions
Question 1: What is the definition of radioactive half-life?
[2 marks]
The time taken for the radioactivity of a sample to reduce by half.
Question 2: Explain what is meant by the statement “radioactive decay is a random process”.
[1 mark]
You cannot predict when an individual nucleus will decay.
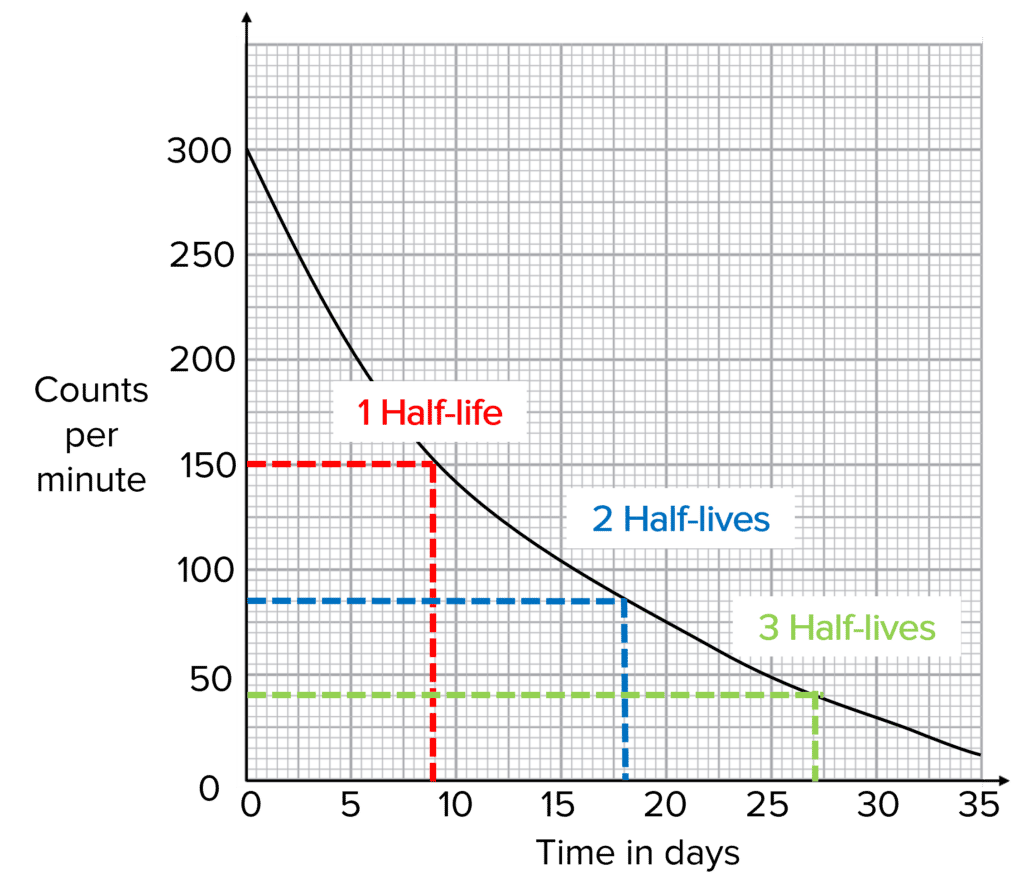
Question 3: A student measures the count rate from an unknown sample and plots their results against time on the following graph. Calculate the half-life of the sample.
[2 marks]
Half of the original counts per minute is \dfrac{140}{2}=\bold{70}
(Using graph) half-life is therefore \bold{1.4}\text{ minutes} (or any value between 1\text{ minutes} and 1.5 \text{ minutes}).
Question 4: A radioactive substance with a half life of 1 \text{ hour} has an activity of 100\text{ Bq}. What is the activity of the substance after 4 \text{ hours}?
[2 marks]
4 \text{ hours} = \bold{4\text{ half-lives}}
100\text{ Bq} \times \dfrac{1}{2} \times \dfrac{1}{2} \times \dfrac{1}{2} \times \dfrac{1}{2} = \bold{6.25\text{ Bq}}
MME Premium Membership
£19.99
/monthLearn an entire GCSE course for maths, English and science on the most comprehensive online learning platform. With revision explainer videos & notes, practice questions, topic tests and full mock exams for each topic on every course, it’s easy to Learn and Revise with the MME Learning Portal.
Sign Up Now