y=mx+c
y=mx+c Revision
The Equation of a Straight Line (y=mx+c)
A straight line graph will always have an equation in the form y=mx+c. You need to be able to work out the equation of a straight line from a graph, as well as manipulate the equation itself.
There are 3 key skills you need to learn involving the equation of a straight line.
Make sure you are familiar with the following topics before continuing.
The Straight Line Equation
Any straight line graph can be described by the following equation:
\textcolor{red}{y}=\textcolor{limegreen}{m}\textcolor{red}{x}+\textcolor{blue}{c}
where \textcolor{red}x and \textcolor{red}y are the coordinates the line passes through, \textcolor{limegreen}m is the gradient and \textcolor{blue}c is the y-intercept (the y-coordinate where the line crosses the y axis).
Skill 1: Finding the Equation of a Straight Line
We need to be able to find the equation of a straight line from the graph.
Example: Find the equation of the straight line graph below
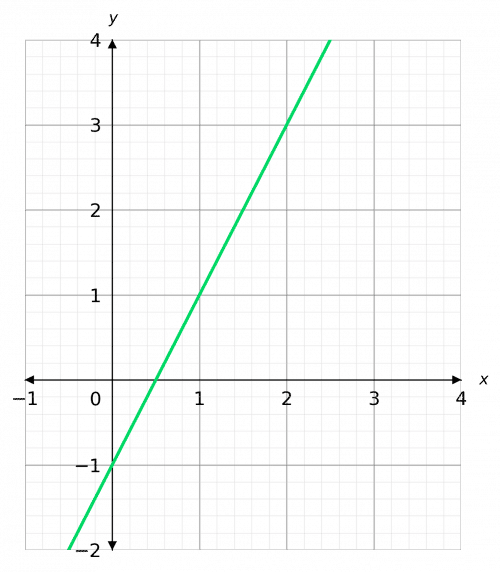
Step 1: Find \textcolor{blue}{c}
We are looking for an equation of the form,
y=\textcolor{limegreen}{m}x+\textcolor{blue}{c}
We know \textcolor{blue}{c} = y-intercept. Looking at the graph, we can see it crosses the axis at - 1, therefore we have \textcolor{blue}{c=-1}.
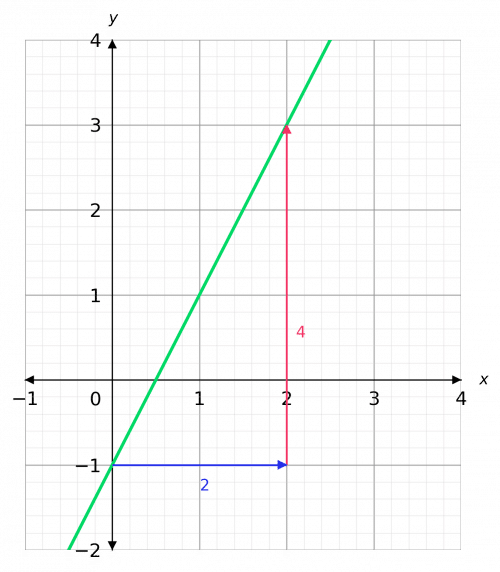
Step 2: Find the gradient (\textcolor{limegreen}{m})
Then, to work out the gradient,
\text{Gradient } = \dfrac{\textcolor{red}{\text{change in }y}}{\textcolor{blue}{\text{change in }x}}
The triangle we have drawn has height 4 and width 2, so we get,
m=\text{gradient}=\dfrac{\textcolor{red}{4}}{\textcolor{blue}{2}}=\textcolor{limegreen}{2}
Therefore, the equation of the straight line is,
y=\textcolor{limegreen}{2}x\textcolor{blue}{-1}
Skill 2: Finding the Equation of a Line Through Two Points
Finding the equation of a straight line between two points is an important skill.
Example: Find the equation of the line that passes through (-3, 1) and (2, -14).
Step 1: Finding the gradient,
m=\text{gradient}=\dfrac{(-14)-1}{2-(-3)}=\dfrac{-15}{5}=-3
Now we know that m=-3, we know that our equation must take the form,
y=-3x+c
Step 2: Substitute the x and y values of one co-ordinate, say x = -3, y=1, into the equation,
1=(-3)\times(-3)+c=9+c
Step 3: Rearrange to solve for c,
c=1-9=-8
Step 4: Now we have all the components of the equation of a line, we can write the resulting equation as,
y=-3x-8
Skill 3: Rearranging Equations into the form y=mx+c
It is often necessary to rearrange the equation of a line to get it in the form y=mx+c. This is essential for finding the gradient and y-intercept.
Example: Find the gradient and y-intercept of the line x+2y=14.
We want to rearrange this equation to make y the subject. So, subtracting x from both sides, we get
2y=-x+14
Then, dividing both sides by 2, we get
y=-\dfrac{1}{2}x+7
Therefore, the gradient is -\dfrac{1}{2} and the y-intercept is 7.
y=mx+c Example Questions
Question 1: Determine the equation of the line shown below.
[2 marks]
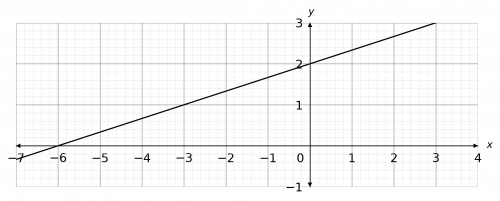
We want an equation of the form
y=mx+c
So, we need to find the gradient, m, and y-intercept, c.
Firstly, looking at the graph we can see that the y-intercept is 2, so c=2.
Now, we will find the gradient by drawing a triangle underneath the line in question.
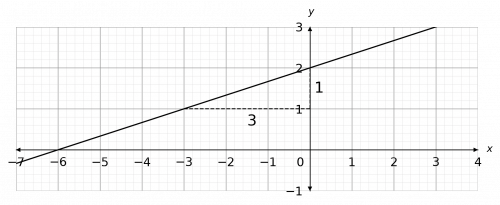
The triangle we have drawn has height 1 and width 3, so we get
m=\text{gradient}=\dfrac{1}{3}
Therefore, the equation of the line is
y=\dfrac{1}{3}x+2
Question 2: Determine the equation of the line that passes through (-3, -6) and (2, 34).
[2 marks]
We want an equation of the form
y=mx+c
So, we need to find the gradient, m, and y-intercept, c.
Firstly, we will find the gradient by dividing the difference in the y coordinates by the difference in the x coordinates:
m=\text{gradient}=\dfrac{-6-34}{-3-2}=\dfrac{-40}{-5}=8
Therefore, the equation of the line is
y=8x+c
Then, to find c we will substitute one pair of coordinates that the line passes through into the equation and rearrange. Here, we’ll pick (2, 34). Subbing this in, we get
34=8\times2+c=16+c
Subtracting 16 from both sides, we get
c=34-16=18
Therefore, the equation of the line is
y=8x+18.
Question 3: Determine the equation of the line shown below.
[2 marks]
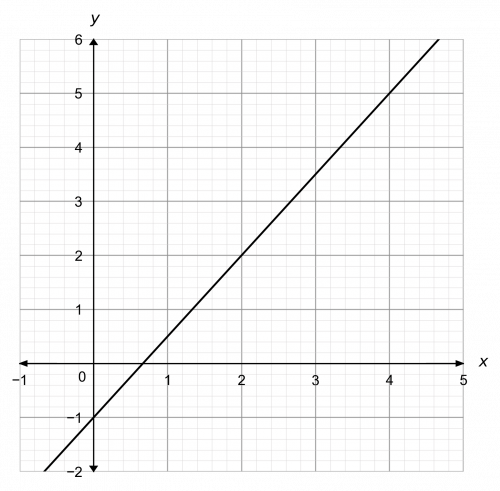
We want an equation of the form
y=mx+c
So, we need to find the gradient, m, and y-intercept, c.
Firstly, looking at the graph we can see that the y-intercept is - 1, so c=-1.
Now, we will find the gradient by drawing a triangle underneath the line in question. Hence
m=\text{gradient}=\dfrac{3}{2}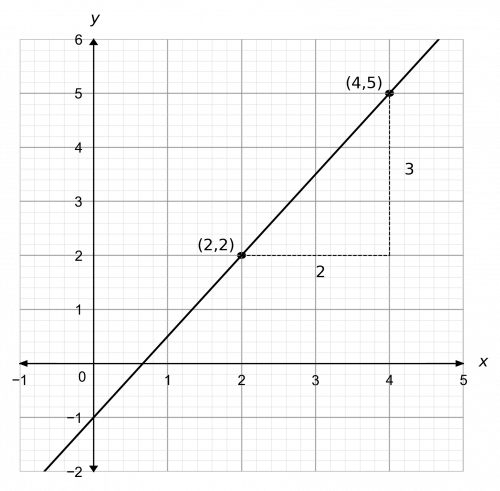
Therefore, the equation of the line is
y=\dfrac{3}{2}x-1





