Revise
Vectors
Vectors Revision
Vectors
A vector is something with both magnitude and direction. On diagrams they are denoted by an arrow, where the length tells us the magnitude and the arrow tells us direction.
- You will need to add and subtract vectors
- You will also need to multiply vectors and understand scalar multiples of vectors
Make sure you are happy with the following topics before continuing:
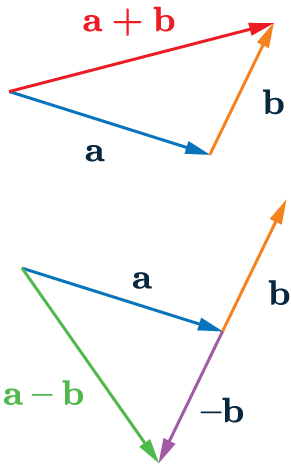
Adding and Subtracting Vectors
When we add vectors:
\textcolor{red}{\mathbf{a}+\mathbf{b}}
this takes you from the start of \mathbf{a} to the end of \mathbf{b} (right).
The negative of a vector has the same magnitude of the original vector, it just goes in the exact opposite direction.
When we subtract vectors:
\textcolor{limegreen}{\mathbf{a}-\mathbf{b}},
we add on the negative of the vector that is being subtracted.
Multiplying Vectors
Multiplying vectors by a Scalar – We can multiply a vector by a number. For example, we can multiply \mathbf{a} by 3:
3\mathbf{\textcolor{red}{a}}=\mathbf{\textcolor{red}{a}}+\mathbf{\textcolor{red}{a}}+\mathbf{\textcolor{red}{a}}
This means the the vectors are added end to end.
We can multiply more complicated vectors
3\mathbf{(\textcolor{red}{a}+\textcolor{blue}{b})}=\mathbf{3\textcolor{red}{a}}+\mathbf{3\textcolor{blue}{b}}
Note: all vectors here are written in bold. When you’re writing this by hand, you should underline each letter that represents a vector.
Scalar multiples – Scalar multiples are all parallel to each other:
\mathbf{3\textcolor{red}{a}}+\mathbf{3\textcolor{blue}{b}} is parallel to \mathbf{\textcolor{red}{a}}+\mathbf{\textcolor{blue}{b}}
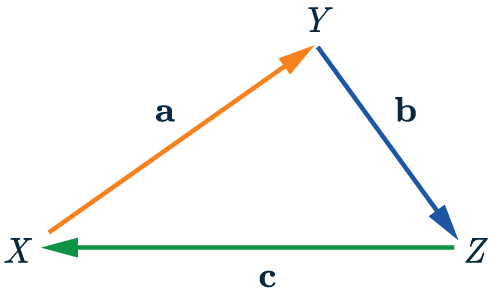
Vector Notation
A vector from point X to point Y will be shown as \overrightarrow{XY}.
So from the diagram shown we can see that:
\overrightarrow{XY} = \mathbf{a}
\overrightarrow{YZ} = \mathbf{b}
\overrightarrow{ZX} = \mathbf{c}
If we go against the arrow the vector becomes negative.
\overrightarrow{YX} = \mathbf{-a}
We can also combine vectors, meaning
\overrightarrow{XZ} = \mathbf{a + b} = \mathbf{-c}
Example: Vectors and Ratios
In the diagram below, we have vectors
\overrightarrow{AB}=3\mathbf{a} and \overrightarrow{AC}=4\mathbf{b} .
Point D lies on the line BC such that BD:DC=1:3.
Write the vector \overrightarrow{AD} in terms of \mathbf{a} and \mathbf{b}.
[3 marks]
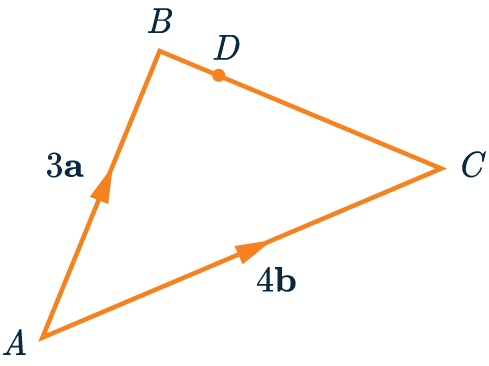
To find \overrightarrow{AD}, we are going to add the vectors
\overrightarrow{AB}+\overrightarrow{BD}
We know \overrightarrow{AB}=3\mathbf{a} but we need to find \overrightarrow{BD}
We know BD:DC=1:3, so the point D is \dfrac{1}{4} of the way along \overrightarrow{BC}
\overrightarrow{BC}=-\overrightarrow{AB}+\overrightarrow{AC}=-3\mathbf{a}+4\mathbf{b}
Now we need to multiply this by \dfrac{1}{4}
\overrightarrow{BD}=\dfrac{1}{4}(3\mathbf{a}+4\mathbf{b})=-\dfrac{3}{4}\mathbf{a}+\mathbf{b}
Now we need to add \overrightarrow{AB} to the answer:
\overrightarrow{AD}=\overrightarrow{AB}+\overrightarrow{BD}=3\mathbf{a}+\left(-\dfrac{3}{4}\mathbf{a}+\mathbf{b}\right)=\dfrac{9}{4}\mathbf{a}+\mathbf{b}
Thus, we have our answer in terms of \mathbf{a} and \mathbf{b}.
Vectors Example Questions
Question 1: The diagram shows a scalene triangle, ABC, with vectors \overrightarrow{AB} =3\mathbf{a} and \overrightarrow{BC}=2\mathbf{b}. The point M is the midpoint of AC.
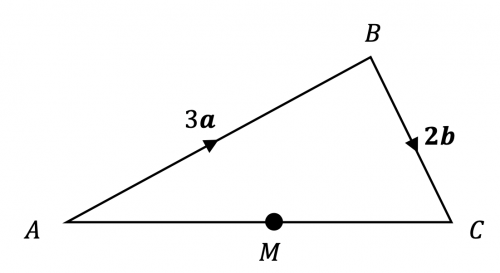
Find an expression for the vector \overrightarrow{AM} in terms of \mathbf{a} and \mathbf{b}.
[3 marks]
First we can find the vector \overrightarrow{AC}
\overrightarrow{AC} =\overrightarrow{AB} +\overrightarrow{BC} =3\mathbf{a} +2\mathbf{b}
Since M is the midpoint of AC we know that \overrightarrow{AM}=\dfrac{1}{2}\overrightarrow{AC}
\overrightarrow{AM}=\dfrac{1}{2}(3\mathbf{a} +2\mathbf{b}) = \dfrac{3}{2}\mathbf{a} +\mathbf{b}
Question 2: The diagram shows a rhombus, ABCD, where the opposite sides are parallel. \overrightarrow{CF} is an extension of \overrightarrow{DC}, such that DC : CF = 5 : 3 and E is the midpoint of AD.
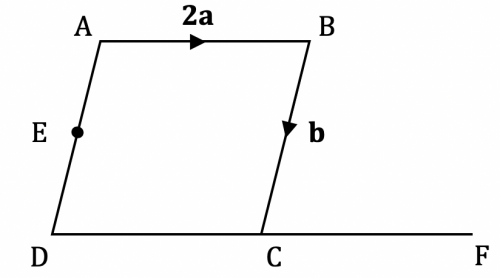
Find an expression for the vector \overrightarrow{EF} in terms of \mathbf{a} and \mathbf{b}.
[3 marks]
The vector \overrightarrow{EF} is the same as:
\overrightarrow{EF}=\overrightarrow{ED}+\overrightarrow{DC}+\overrightarrow{CF}
First, we can find the vector \overrightarrow{ED} as \dfrac{1}{2}\mathbf{b} .
Then we also know \overrightarrow{DC} = \overrightarrow{AB}, hence \overrightarrow{DC}=2\mathbf{a} .
The final section \overrightarrow{CF} = \dfrac{3}{5}\times 2\mathbf{a}=\dfrac{6}{5}\mathbf{a}
Hence,
\overrightarrow{EF}= \dfrac{1}{2} \mathbf{b}+2\mathbf{a}+\dfrac{6}{5}\mathbf{a}=3.2\mathbf{a}+ \dfrac{1}{2} \mathbf{b}
Question 3: The diagram shows a scalene triangle, ABC, with vectors \overrightarrow{AB} =\mathbf{a} and \overrightarrow{AC}=2\mathbf{b}. The point D is positioned on the line BC such that BD : DC = 3 : 2 . The point E is positioned on the line AD such that AE : ED = 1 : 2 .
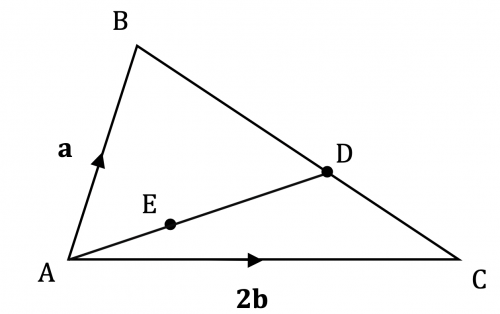
Find an expression for the vector \overrightarrow{AE} in terms of \mathbf{a} and \mathbf{b}.
[3 marks]
First we can find the vector \overrightarrow{BC}
\overrightarrow{BC} =-\overrightarrow{AB} +\overrightarrow{AC} =-\mathbf{a} +2\mathbf{b}
Then we can find:
\overrightarrow{BD} =\dfrac{3}{5}\overrightarrow{BC} =-\dfrac{3}{5}\mathbf{a} +\dfrac{6}{5}\mathbf{b}
Next:
\begin{aligned} \overrightarrow{AD} &=\overrightarrow{AB}+\overrightarrow{BD} \\ &=\mathbf{a} +\bigg(-\dfrac{3}{5}\mathbf{a} +\dfrac{6}{5}\mathbf{b}\bigg) \\ & =\dfrac{2}{5}\mathbf{a}+\dfrac{6}{5}\mathbf{b} \end{aligned}
Finally:
\begin{aligned} \overrightarrow{AE} &=\dfrac{1}{3}\overrightarrow{AD} \\ &=\dfrac{1}{3}\bigg(\dfrac{2}{5}\mathbf{a}+\dfrac{6}{5}\mathbf{b}\bigg) \\ &= \dfrac{2}{15}\mathbf{a}+\dfrac{2}{5}\mathbf{b} \end{aligned}
Question 4: The diagram shows a regular hexagon, ABCDEF, centre O, with with vectors \overrightarrow{OB} =\mathbf{a} and \overrightarrow{ED}=\mathbf{b}.
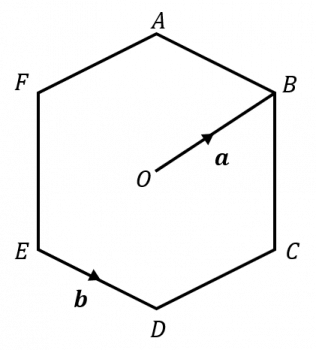
Find an expression for the vector \overrightarrow{AC} in terms of \mathbf{a} and \mathbf{b}.
[3 marks]
We will find \overrightarrow{AC} by doing,
\overrightarrow{AC}=\overrightarrow{AB}-\overrightarrow{OB}+\overrightarrow{OC}
Thus
\overrightarrow{AC} =\mathbf{b}-\mathbf{a}+\mathbf{b}= 2\mathbf{b}-\mathbf{a}
Question 5: The diagram below shows the vectors \overrightarrow{AE}=3\mathbf{a}-2\mathbf{b} and \overrightarrow{DC}=2\mathbf{a}+4\mathbf{b}. The points E and B are the midpoints of AD and AC respectively.
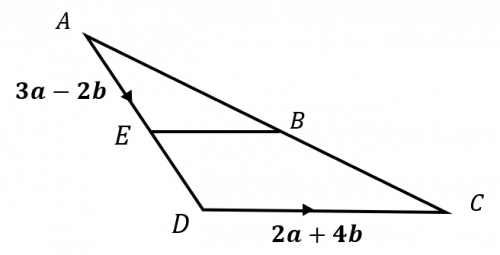Find an expression for \overrightarrow{EB} in terms of \mathbf{a} and \mathbf{b} and state whether or not it is parallel to \overrightarrow{DC}.
[4 marks]
We will find \overrightarrow{EB} by doing
\overrightarrow{EB}=\overrightarrow{EA}+\overrightarrow{AB}
The first vector is straightforward, because we know \overrightarrow{AE}, and that is just the same vector in the opposite direction. So, we get:
\overrightarrow{EA}=-\overrightarrow{AE}=-(3\mathbf{a}-2\mathbf{b})=-3\mathbf{a}+2\mathbf{b}
Now we need \overrightarrow{AB}. Since B is the midpoint of AC (given in the question), we must have that \overrightarrow{AB}=\frac{1}{2} \overrightarrow{AC}. Therefore, looking at the diagram, we get that:
\overrightarrow{AB}=\dfrac{1}{2}\overrightarrow{AC}=\dfrac{1}{2}\left(\overrightarrow{AD}+\overrightarrow{DC}\right)
We’re given the second part of this, \overrightarrow{DC}=2\mathbf{a}+4\mathbf{b}, and since E is the midpoint of AD, we can also work out the first part:
\overrightarrow{AD}=2\overrightarrow{AE}=2(3\mathbf{a}-2\mathbf{b})=6\mathbf{a}-4\mathbf{b}
Now, we have everything we need and can go back through our work, filling in the gaps we find:
\overrightarrow{AB}=\dfrac{1}{2}\left(6\mathbf{a}-4\mathbf{b}+2\mathbf{a} +4\mathbf{b}\right)=\dfrac{1}{2}\left(8\mathbf{a}\right)=4\mathbf{a}
Finally we have that:
\overrightarrow{EB}=\overrightarrow{EA}+\overrightarrow{AB}=-3\mathbf{a}+2\mathbf{b}+4\mathbf{a}=\mathbf{a}+2\mathbf{b}
If \overrightarrow{EB} and \overrightarrow{DC} are parallel, then one must be a multiple of the other. Well, if we multiply \overrightarrow{EB} by 2 then,
2\times\overrightarrow{EB}=2(\mathbf{a}+2\mathbf{b})=2\mathbf{a}+4\mathbf{b}=\overrightarrow{DC}
We have shown that 2\overrightarrow{EB}=\overrightarrow{DC}, therefore, the two lines must be parallel.
Vectors Worksheet and Example Questions
(NEW) Vectors Exam Style Questions - MME
Level 6-7GCSENewOfficial MME
