Using and Making Formulas
Using and Making Formulas Revision
Using and Making Formulas
Formulas are extremely useful in maths. They tell us how to calculate new values based on information we already know.
Using formulas is relatively easy but making formulas for yourself can sometimes be tricky.
Skill 1: Using Formulas
A formula is a rule that helps you work something out. For example, the formula for converting from kilograms (k) to pounds (p) is:
p=2.2k
We can use this formula to convert any value from kilograms to pounds by simply replacing the k with our value. This is known as substitution.
Example: Convert 5 kilograms into pounds.
We should rewrite the formula, then we need to substitute our value of 5 into it:
\begin{aligned}p &= 2.2 \times k \\ p &= 2.2 \times 5 \\ p &= 11\end{aligned}
Therefore 5 kilograms is equal to 11 pounds.
Skill 2: Making Formulas from Words
Sometimes you may be asked to give an expression or a formula. An expression is similar to a formula, but does not feature an equals sign (=).
Example: A taxi company charges £3 as a base fee plus an additional £0.50 per minute.
If we want to construct a formula to represent this information, we need to define a couple of things. Let the total cost of the journey be \textcolor{red}C and the time of the journey be \textcolor{blue}t.
We can now use these values to construct our formula:
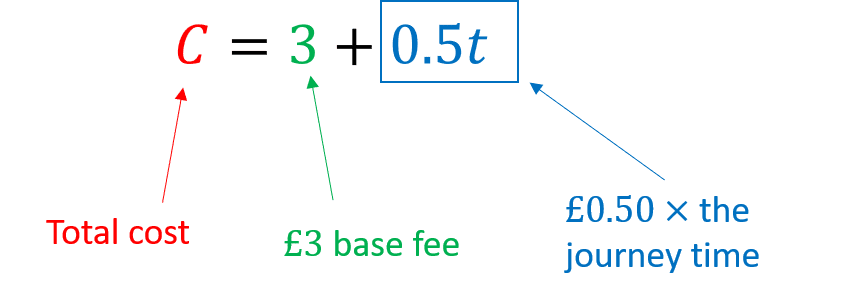
Notes:
Having a good understanding of BIDMAS is important when constructing formulas as you need to make sure you get things in the right order.
Example 1: Using a Formula
The formula to convert temperature from degrees Celsius (\textcolor{blue}C) to degrees Fahrenheit (\textcolor{red}F) is:
\textcolor{red}{F} = \bigg(\dfrac{9}{5}\bigg)\textcolor{blue}{C} + 32
Convert 25 degrees Celsius (\textcolor{blue}{C}) into degrees Fahrenheit (\textcolor{red}{F}).
[2 marks]
We need to substitute the value of \textcolor{blue}{25} into the formula:
\begin{aligned}\textcolor{red}{F} &= \bigg(\dfrac{9}{5}\bigg) \times \textcolor{blue}{25} + 32 \\ \textcolor{red}{F} &= (9\times5) +32 \\ \textcolor{red}{F} &= 45+32 \\ \color{red} F &= 77\end{aligned}
So 25 degrees Celsius is equal 77 degrees Fahrenheit.
Example 2: Making a Formula to Solve a Problem
A car salesperson earns a salary of £20000 per year and earns a bonus of £250 per car sold.
If the salesperson earns £25500 in one year, how many cars did they sell?
[3 marks]
First we need to construct a formula to represent this information. Let the number of cars sold be n, and the total amount the salesperson earned in the year be E:
E = 20000 + 250n
Now we can substitute in the value of £25500 in place of E:
25500 = 20000 + 250n
Now we have an equation which we need to rearrange to get the value of n:
\begin{aligned}25500 &= 20000 + 250n \\ 25500-20000 &= 250n \\ 5500 &= 250 n \\ 5500 \div 250 &= n \\ n &=22\end{aligned}
So, the salesperson sold 22 cars.
Using and Making Formulas Example Questions
Question 1: Consider the following formula:
q = 4p - 6
Work out the value of q when p=6
[1 mark]
Substitute the value of p=6 into the formula:
\begin{aligned} q &= 4p-6 \\ q &= 4\times6-6 \\ q&=24-6 \\ q &= 18 \end{aligned}
Question 2: A persons Body Mass Index (BMI) can be calculated using the following formula:
\text{BMI} = \dfrac{m}{h^2}
Where m is the mass of the person in kilograms and h is the height of the person in metres m.
Calculate the BMI of a person with a height of 1.6 m and a mass of 80 kg.
[2 marks]
Substitute the values h = 1.6 and m = 80 into the formula:
\begin{aligned} \text{BMI} &= \dfrac{80}{1.6^2} \\[1.5em] \text{BMI} &= \dfrac{80}{2.56} \\[1.5em] \text{BMI} &= 31.25\end{aligned}
So the person has a BMI of 31.25
Question 3: There are blue, red and green sweets in a bag.
There are 3 blue sweets and x red sweets.
There are 2 more green sweets than there are red sweets.
Give an expression for the number of sweets in the bag.
[2 marks]
There are 2 more green sweets than there are red sweets, and there are x red sweets. So the number of green sweets is:
x+2
So there are 3 blue sweets, plus x red sweets, plus x+2. Combining these gives the following expression:
3+x+(x+2)
Which can be simplified by collecting like terms to:
5+2x
Question 4: A person loses 1.1 g of sodium per litre of sweat.
The same person loses 1.5 litres of water from sweating per hour of exercise.
Write a formula to relate the sodium loss (S) to the water loss (W) and the time (in hours) spent exercising (t)
(This is a difficult question!)
[3 marks]
The amount of sodium lost (S) can be found by multiplying the loss per litre by the number of litres lost (W):
S=1.1\times W
The amount of water lost (W) can be found by multiplying the loss per hour by the time spent exercising (t):
W = 1.5 \times t
Now we need to combine the two expressions by substituting our expression for W into our expression for S:
\begin{aligned}S &= 1.1 W \\ S &=1.1 \times (1.5t)\\ &=S= 1.65 t \end{aligned}
Question 5: A plumber charges a fixed fee of £40 for each repair job and an additional £9.50 per hour of work (h).
Write a formula for the total cost (C) of a repair job and use it to work out the number of hours spent working if the plumber earns £68.5 in a single repair job.
[3 marks]
Our formula needs to add the base cost of £40 to the hourly rate of £9.50. Our formula is therefore:
C = 40 + 9.5h
If the plumber earns £68.50 in a single repair job, we can substitute this into our formula and rearrange to get h:
\begin{aligned} 68.5 &= 40+9.5h \\ (-40)\quad 28.5 &= 9.5 h \\ (\div9.5)\quad 3 &= h \end{aligned}
So the repair job took 3 hours.

MME Premium Membership
£19.99
/monthLearn an entire GCSE course for maths, English and science on the most comprehensive online learning platform. With revision explainer videos & notes, practice questions, topic tests and full mock exams for each topic on every course, it’s easy to Learn and Revise with the MME Learning Portal.
Sign Up Now
