Revise
Trigonometry Common Values
Trigonometry Common Values Revision
Trigonometry Common Values
Up to this point, we’ve let our calculators do the heavy lifting when it comes to evaluating the 3 trigonometry functions, but there are some values of the trigonometry functions that you have to remember.
Make sure you are happy with the following topics before continuing:
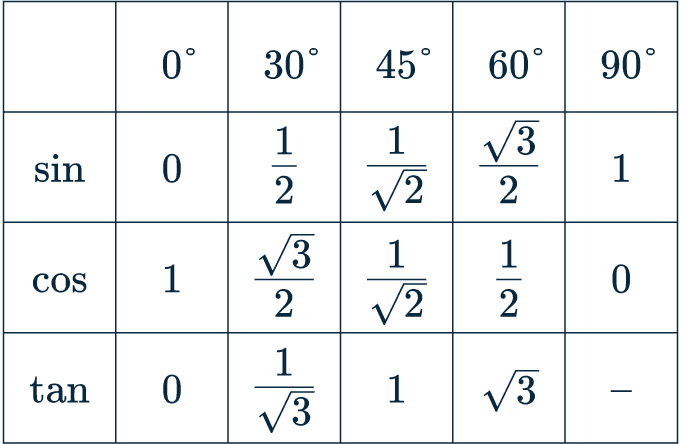
Values You Need to Learn
Specifically, you will have to remember:
\sin, \cos, and \tan of 0\degree, 30\degree, 45\degree, 60\degree, and 90\degree
You need to remember all of these values.
Trigonometric Triangles
Remembering the values in the table may be a little tricky if you don’t have a photographic memory so you might find it easier to remember two important triangles:
- Equilateral Triangle (cut in half)
- Right Angle Isosceles Triangle
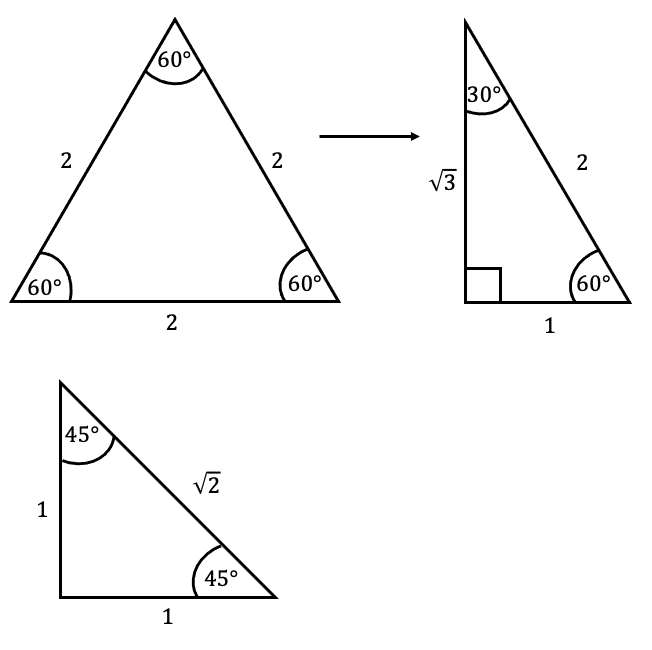
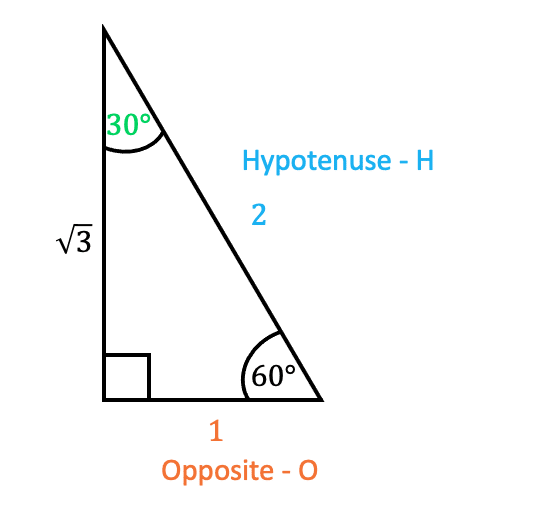
To use these triangles, we use SOH-CAH-TOA rules to calculate common trigonometry values.
For instance, say we wanted to know \sin{30}, we use the rule
\sin{\textcolor{#00d865}{x}}=\dfrac{\textcolor{#f95d27}{O}}{\textcolor{#10a6f3}{H}}
and take the corresponding values from the triangle that we need.
\sin{\textcolor{#00d865}{30}}=\dfrac{\textcolor{#f95d27}{1}}{\textcolor{#10a6f3}{2}}
Transition Maths Cards
The transition maths cards are a perfect way to cover the higher level topics from GCSE whilst being introduced to new A level maths topics to help you prepare for year 12. Your ideal guide to getting started with A level maths! The profit from every pack is reinvested into making free content on MME, which benefits millions of learners across the country.
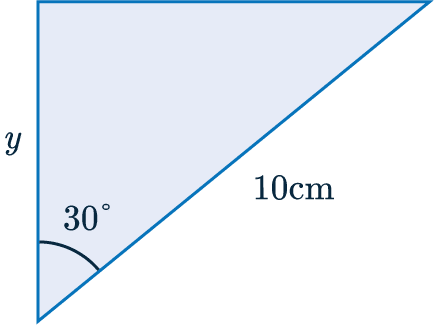
Example
Find the value of y shown on the right-angled triangle.
[2 marks]
First we have to find which equation we need to use.
The hypotenuse =\textcolor{blue}{10} cm
The adjacent = \textcolor{limegreen}{y}
This means we use \textcolor{purple}{C}\textcolor{limegreen}{A}\textcolor{blue}{H}
\textcolor{purple}{\cos(30\degree)} = \dfrac{\textcolor{limegreen}{y}}{\textcolor{blue}{10}}
We can see in the table that \textcolor{purple}{\cos(30\degree)} = \textcolor{purple}{\dfrac{\sqrt{3}}{2}}, putting this into the equation we can solve for \textcolor{limegreen}{y}.
\textcolor{purple}{\dfrac{\sqrt{3}}{2}} = \dfrac{\textcolor{limegreen}{y}}{\textcolor{blue}{10}}
\dfrac{\textcolor{blue}{10}\textcolor{purple}{\sqrt{3}}}{\textcolor{purple}{2}} = \textcolor{limegreen}{y}
5\sqrt{3} = \textcolor{limegreen}{y}
Trigonometry Common Values Example Questions
Question 1: Work out the exact value of \sin(60\degree)+ \cos(30\degree) without the use of a calculator.
[2 marks]
Each term is one of a small list of common trigonometry values that students are required to remember. Here,
\sin(60\degree)=\dfrac{\sqrt{3}}{2}
as well as,
\cos(30\degree)=\dfrac{\sqrt{3}}{2}
Thus the calculation is,
\sin(60\degree)+ \cos(30\degree)=\dfrac{\sqrt{3}}{2}+\dfrac{\sqrt{3}}{2}=\sqrt{3}
Question 2: Work out the exact value of,
\dfrac{\tan(45\degree)}{\sin(30\degree)} \times 10\tan(60\degree)
[2 marks]
Each term is one of a small list of common trigonometry values that students are required to remember:
\tan(45\degree)=1
\sin(30\degree)=\dfrac{1}{2}
and
\tan(60\degree)=\sqrt{3}
Thus the calculation is,
\dfrac{\tan(45\degree)}{\sin(30\degree)} \times 10\tan(60\degree)=\dfrac{1}{\frac{1}{2}} \times 10(\sqrt{3})=2\times10\sqrt{3}=20\sqrt{3}
Question 3: Work out the exact value of,
\dfrac{\tan(45\degree)+\cos{(30\degree)}}{\tan(45\degree)} \times \cos(60\degree)
[2 marks]
Each term is one of a small list of common trigonometry values that students are required to remember:
\tan(45\degree)=1
\cos(30\degree)=\dfrac{\sqrt{3}}{2}
and
\cos(60\degree)=\dfrac{1}{2}
Thus the calculation is,
\dfrac{\tan(45\degree)+\cos{(30\degree)}}{\tan(45\degree)} \times \cos(60\degree)=\dfrac{1+\frac{\sqrt{3}}{2}}{1} \times \dfrac{1}{2}=\dfrac{2+\sqrt{3}}{2}\times \dfrac{1}{2}=\dfrac{2+\sqrt{3}}{4}
Question 4: ABC is a right-angled triangle. Work out the missing side length x without the use of a calculator.
[2 marks]
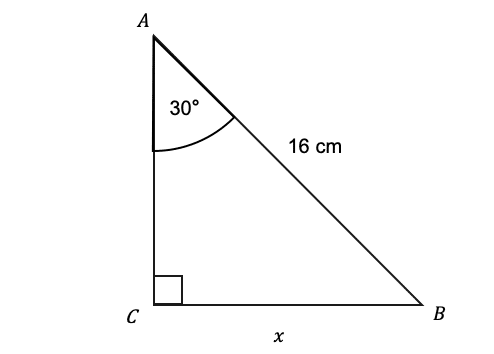
This question requires the use of Pythagoras. We are given the hypotenuse and want the find the opposite side length, hence,
\sin(30\degree)=\dfrac{x}{16}
Thus to find x we simply multiply both sides by 16 and use the common trigonometry value of \sin(30\degree) =\dfrac{1}{2}
x=16\times\sin(30\degree)=16\times \dfrac{1}{2}=8 cm.
Question 5: ABC is a right-angled triangle. Work out the missing side length x without the use of a calculator.
[2 marks]
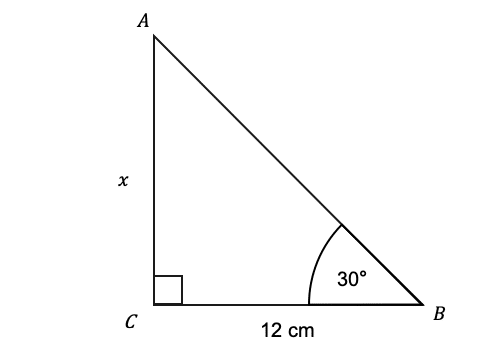
This question requires the use of Pythagoras. We are given the adjacent length and want the find the opposite side length, hence,
\tan(30\degree)=\dfrac{x}{12}
Thus to find x we multiply both sides by 12 and use the common trigonometry value of \tan(30\degree) =\dfrac{1}{\sqrt{3}}
x=12\times\tan(30\degree)=12\times \dfrac{1}{\sqrt{3}}=12\times \dfrac{\sqrt{3}}{3}=4\sqrt{3} cm.
Trigonometry Common Values Worksheet and Example Questions
(NEW) Trig Common Values Exam Style Questions - MME
Level 4-5NewOfficial MME
