Revise
Solving Quadratics Through Factorising
Solving Quadratics Through Factorising Revision
Solving Quadratic Equations by Factorising
Quadratics are algebraic expressions that include the term, x^2, in the general form,
ax^2 + bx + c
If you are on the foundation course, any quadratic equation you’re expected to solve will always have a=1, with all terms on one side and a zero on the other. If you are on the higher course, you may have to do some rearranging in order to get all the terms on one side. Make sure you are happy with the following topics before continuing.
Solving through Factorising (a=1)
We can solve quadratics through factorising by following these 4 easy steps.
Example: Solve the quadratic equation, \textcolor{blue}{ x^2-3x+2=0} by factorisation.
- Step 1: Factorise the quadratic \textcolor{blue}{(x -2)(x-1)=0}
- Step 2: Form two linear equations
Since the right-hand side of the equation is zero, the result of multiplying the two brackets together on the left-hand side must be zero. Therefore, at least one of the brackets must be equal to zero. So, in summary,
If (x-2)(x-1)=0, then either (x-2)=0 or (x-1)=0.
- Step 3: Solve the equations to find the roots of the equation
Equation 1:
\begin{aligned}(+2) \,\,\,\,\,\,\,\,\, x - 2 &= 0 \\ x &= 2\end{aligned}
Equation 2:
\begin{aligned}(+1) \,\,\,\,\,\,\,\,\, x - 1 &= 0 \\ x &= 1\end{aligned}
The final roots are:
x = 2 \,\,\,\,\text{and}\,\,\,\, x=1
Note: The solutions to a quadratic equation are also called roots, because they correspond to where a quadratic graph crosses the x-axis.
Solving through Factorising (a>1)
Solve the following quadratic equation through factorising 2x^2-3x-9=0
Step 1: Rearrange the given quadratic so that is it equal to zero (=0)
This quadratic is already equal to 0 so there is nothing more to do.
Step 2: Factorise the quadratic,
(2x+3)(x-3)=0
Step 3: Form two linear equations
2x+3=0 \,\,\text{and}\,\, x-3=0
Step 4: Solve the equations to find the roots of the equation
Equation 1:
\begin{aligned}(-3)\,\,\,\,\,\,\,2x+3&=0 \\ (\div2)\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,2x&=-3 \\ \,\,\,\,\,\,\,\,\, x& = -\dfrac{3}{2}\end{aligned}
Equation 2:
\begin{aligned}(+3)\,\,\,\,\,\,\,\,\,x-3&=0 \\ x &=3 \end{aligned}
So, the 2 solutions to the equation are x=3 and x=-\frac{3}{2}.
Quadratic Equations and Sketching Graphs
It is possible to use factorisation to allow you to sketch a quadratic graph.
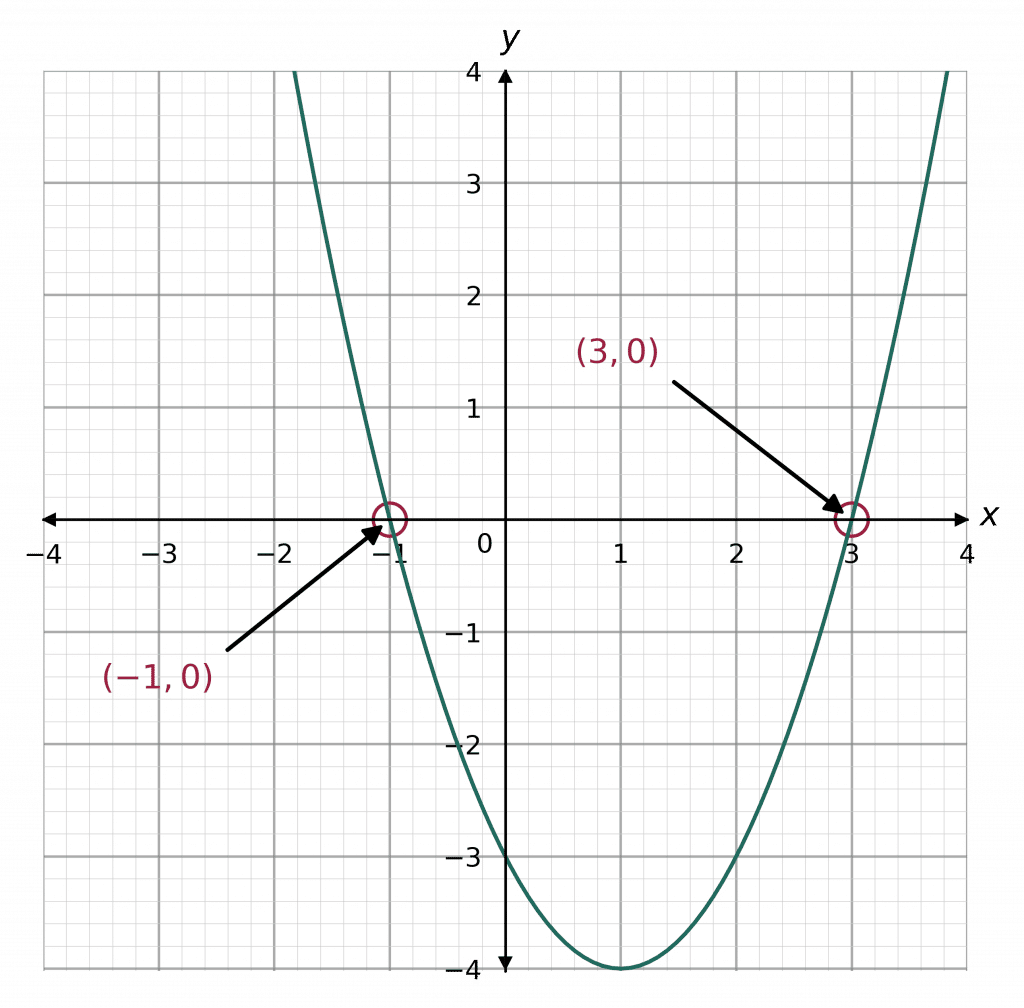
Example: Use factorisation to find the roots of x^2 -2x -3=0 and hence sketch the quadratic.
Like always, the equation needs to be =0
Step 1: First we need to factorise the left hand side of the equation
(x-3)(x+1) = 0
Step 2: Solve the quadratic as show in the above examples
\begin{aligned}(+3)\,\,\,\,\,\,\,\,\,x-3&=0 \\ x&=3\end{aligned}
\begin{aligned}(-1) \,\,\,\,\,\,\,\,\,x+1&=0 \\ \,\,\,\,\,\,\,\,\, x&=-1\end{aligned}
Step 3: Find the coordinates of the roots. We know this equation has the solutions x= 3 and x=-1
When we set the equation to 0, y=0. This means we can form the two coordinates
(3,0) and (-1,0)
Step 4: Identify the y-intercept. This is the point at which the curve crosses the y-axis and is given by the value of c in the general quadratic ax^2 + bx +c=0, which in this case is -3.
Once you have found these values, you can sketch the graph, see below.
Note: This graph was done by a computer, but a “sketch” doesn’t have to be perfect, it just has to be the right shape and cross the axes at the right points.
Solving Quadratics Through Factorising Example Questions
Question 1: Use factorisation to solve the equation p^2-3p-10=0
[3 marks]
The quadratic on the left hand side of the equation factorises so that,
p^2-3p-10=(p+2)(p-5)
Therefore, we can rewrite the equation as
(p+2)(p-5)=0
For the left-hand side to be zero we require one of the brackets to be zero, hence, the two solutions to this quadratic equation are,
p=-2 and p=5
Question 2: Use factorisation to solve the equation x^2-8x+15=0
[3 marks]
The quadratic on the left hand side of the equation factorises so that,
x^2-8x+15=(x-5)(x-3)
Therefore, we can rewrite the equation as
(x-5)(x-3)=0
For the left-hand side to be zero we require one of the brackets to be zero, hence, the two solutions to this quadratic equation are,
x=5 and x=3
Question 3: Use factorisation to find the roots of the quadratic x^2-6x+8
[3 marks]
To find the roots of a quadratic, we must set it equal to zero and find the solutions of that equation,
x^2-6x+8=0
Now, we must factorise. Observing that (-2)\times(-4)=8 and -2+(-4)=-6, we get that this quadratic factorises to
(x-2)(x-4)=0
So, for the left-hand side to be zero we require one of the brackets to be zero.
Therefore, the two roots of this quadratic equation are
x=2 and x=4
Question 4: Use factorisation to solve the equation 2x^2+13x+9=-6
[4 marks]
First rearrange the equation so that it equals 0.
2x^2+13x+15=0
The quadratic on the left hand side of the equation factorises so that,
2x^2+13x+15=(2x+3)(x+5)=0
For the left-hand side to be zero we require one of the brackets to be zero, hence, the two solutions to this quadratic equation are,
x=-\dfrac{3}{2} and x=-5
Question 5: Use factorisation to solve the equation 3k^2+17k-6=0
[4 marks]
The quadratic on the left hand side of the equation factorises so that,
(3k-1)(k+6)=0
So, for the left-hand side to be zero we require one of the brackets to be zero. If the first bracket is zero, then we get
3k-1=0
If we add 1 to both sides and then divide by 3, we get the solution
k=\dfrac{1}{3}
If the second bracket is zero, then we get
k=-6
Therefore, the two solutions to this quadratic equation are,
k=\frac{1}{3} and k=-6
Solving Quadratics Through Factorising Worksheet and Example Questions
(NEW) Solving Quadratics By Factorisation Exam Style Questions - MME
Level 4-5GCSENewOfficial MMESolving Quadratics Through Factorising Drill Questions
Solving Quadratics By Factorising - Drill Questions
Level 4-5GCSE
Solving Quadratics By Factorising (2) - Drill Questions
Level 4-5GCSE
