Set Notation
Set Notation Revision
Set Notation
In maths, a set is a collection of things, usually numbers. Sets are often abbreviated as a capital letter. Venn diagrams and inequalities link in with sets so make sure you are happy with the following topics before continuing:
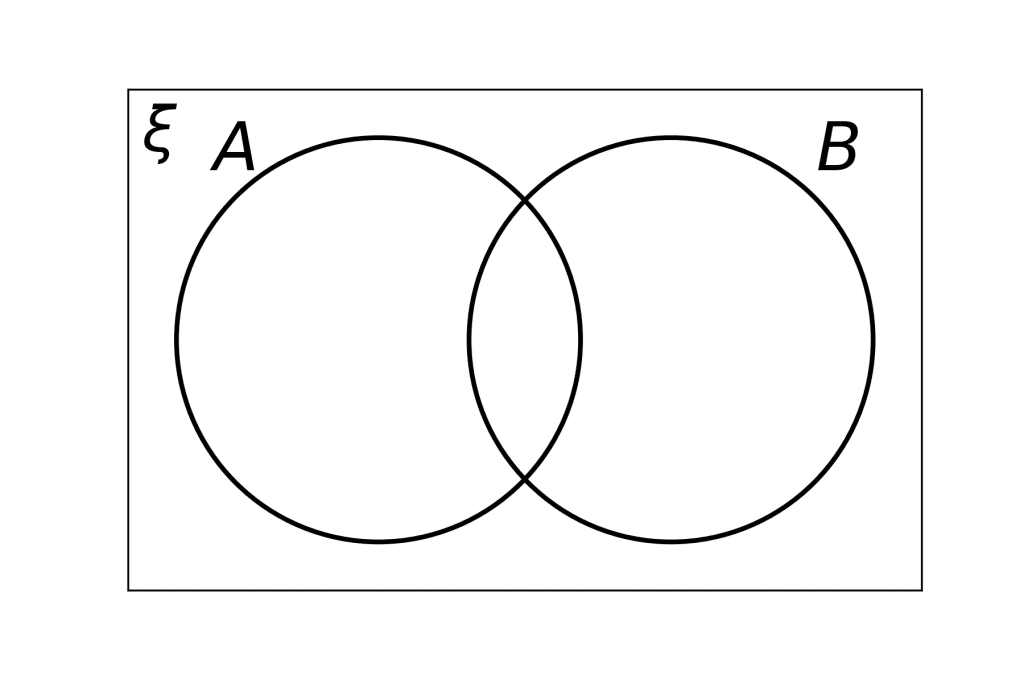
Understanding Set Notation
Sets are often denoted using the curly brackets { }, for example the set of the first 5 odd numbers would be written with a capital such that, A=\{1, 3, 5, 7, 9\}.

It is easier to visualise multiple sets by using Venn diagrams. If we were given another set B then we can place the values of set B in circle B, and all the values of set A in circle A.
Any values that appear in both set A and set B should be placed in the intersection being careful not duplicate any values.
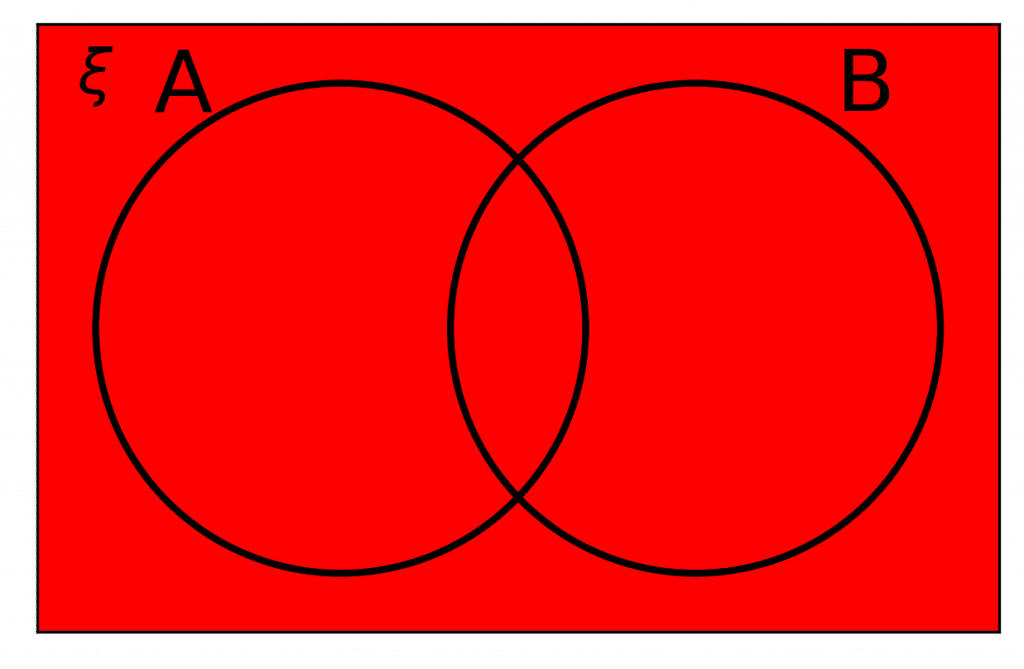
The Universal Set: \xi

The universal set is everything inside the rectangle and is represented by the Greek letter “xi”, \textcolor{red}{ \xi }. It means all values that are to be included must be placed within the rectangle.
Note: If any numbers that are included but are neither within set \textcolor{limegreen}{A} nor set \textcolor{blue}{B}, they must go outside of the circles but inside the rectangle.
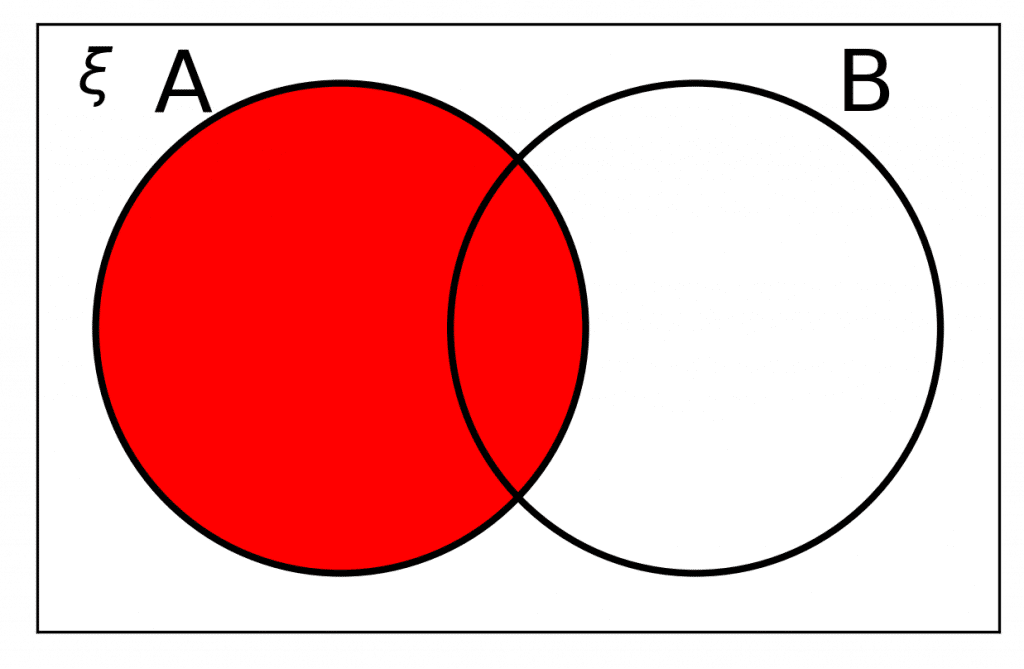
Notation Rule 1: A

A means everything that is contained only in \textcolor{limegreen}{A}.
Similarly if the question asked for everything inside \textcolor{blue}{B} it would be the entirety of \textcolor{blue}{B} that would need to be shaded.
n(A) refers to the number of elements within set \textcolor{limegreen}{A}. So if there were 4 numbers inside circle \textcolor{limegreen}{A}, then n(A)=4
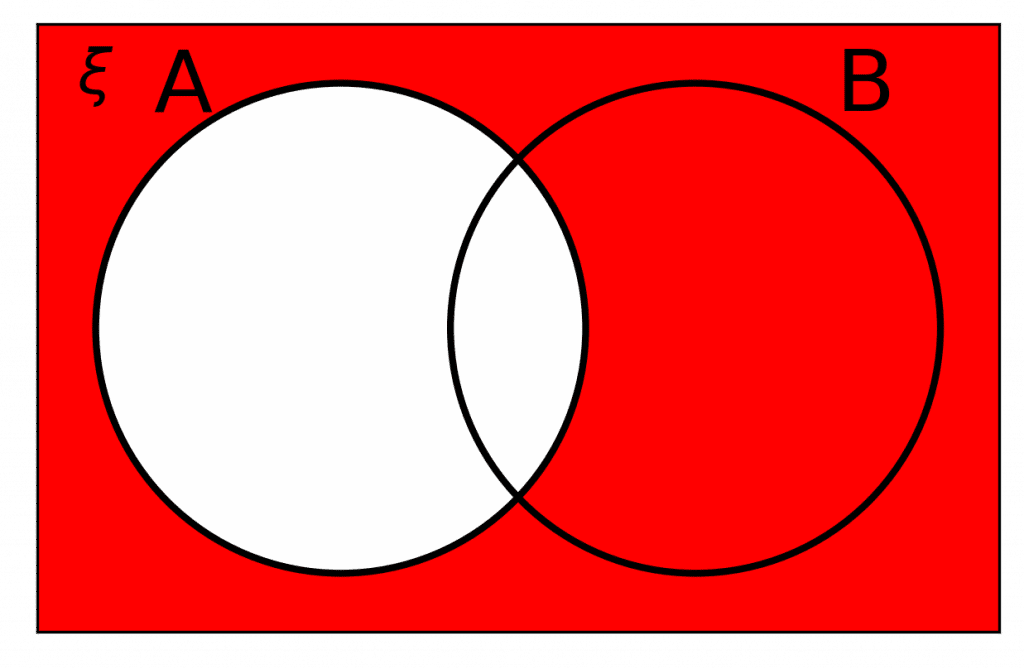
Notation Rule 2: A'

A ' means not in \bm{A}.
It is a new set of all the elements from the universal set that do not appear in \textcolor{limegreen}{A}. Similarly for \textcolor{blue}{B} we can write B' to express elements that are not in \textcolor{blue}B.
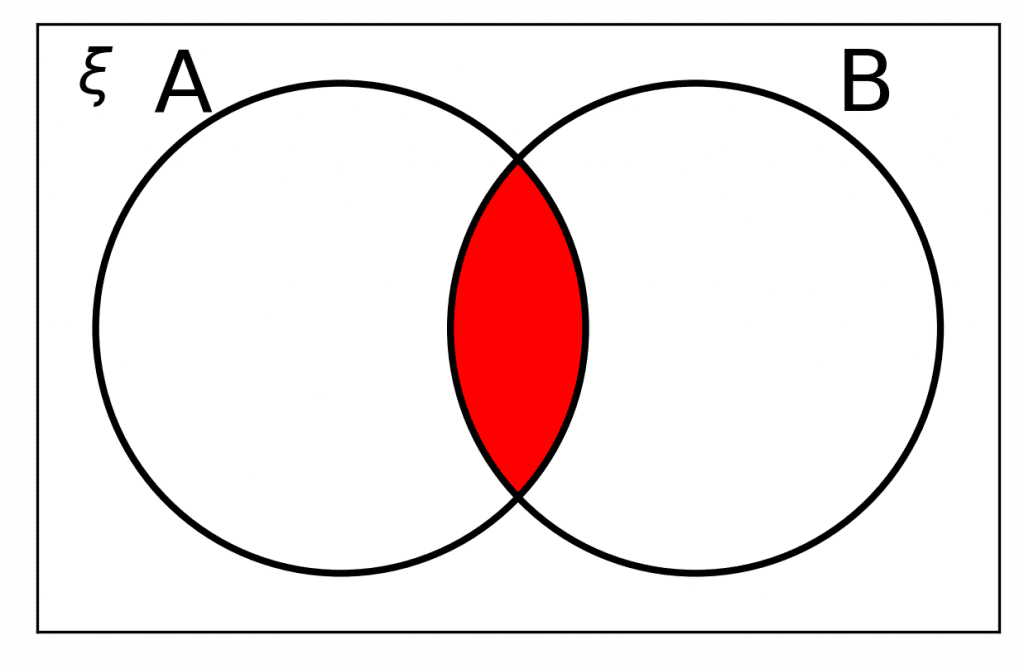
Notation Rule 3: A \cap B

A \cap B means \bm{A} and \bm{B}
|t is a new set that contains only elements that are in both \textcolor{limegreen}{A} and \textcolor{blue}{B}, i.e. the elements where \textcolor{limegreen}{A} and \textcolor{blue}{B} intersect.
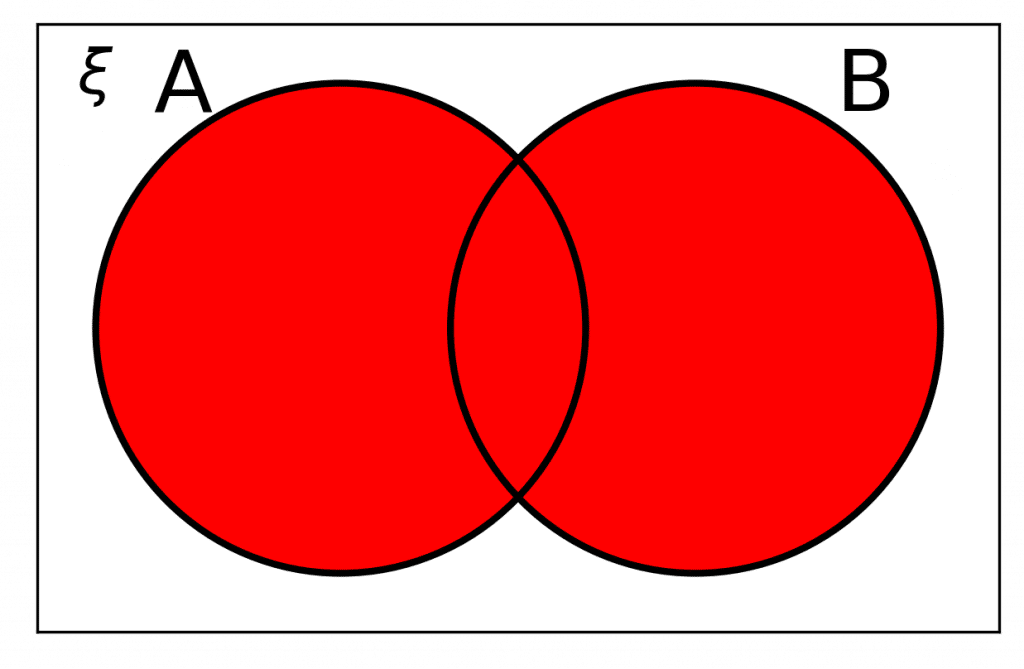
Notation Rule 4: A \cup B

A \cup B means \bm{A} or \bm{B}.
It is a new set that contains any elements that are in either \textcolor{limegreen}{A} or \textcolor{blue}{B}.
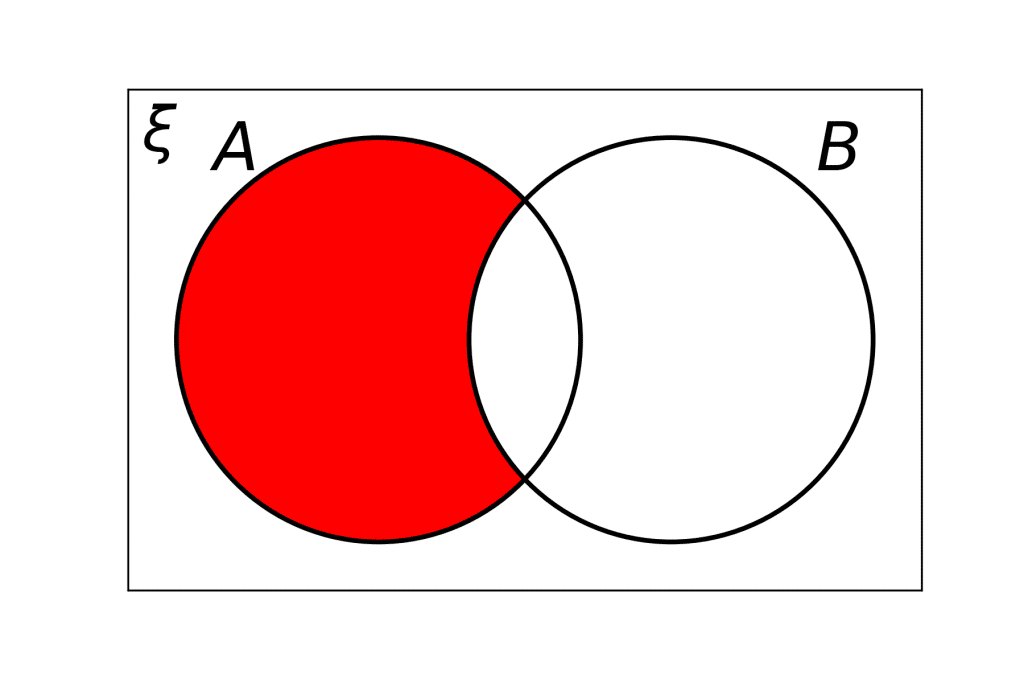
Notation Rule 5: A \cap B'

A \cap B' means \bm{A} and not \bm{B}.
It is a new set that contains any elements that are in \textcolor{limegreen}{A} but not in \textcolor{blue}{B}.
Set Notation for Inequalities
The other time set notation appears is when working with inequalities. The good news is, it’s pretty straightforward! To write the inequality x \leq 5 in set notation, we write
\{x : x\leq 5\}
So, you have to add 3 things: curly brackets, the variable, and a colon.
Example 1: Set Notation
Let A=\{1, 2, 3, 8, 10, 12\} and B=\{6, 5, 4, 3, 2, 10\}. Write down the set
a) \, A\cap B
b) \, A\cup B
[2 marks]
a) A\cap B contains every element that appears in both A and B.
Looking at the sets, we see that there are three of them: 2, 3, and 10. Therefore, we have
A\cap B=\{2, 3, 10\}
b) A\cup B contains all the elements that are in either A or B. We have
A \cup B=\{1, 2, 3, 4, 5, 6, 8, 10, 12\}
Note: When a number appears in both sets, we don’t need to write it in twice.
Example 2: Sets Notation and Venn Diagrams
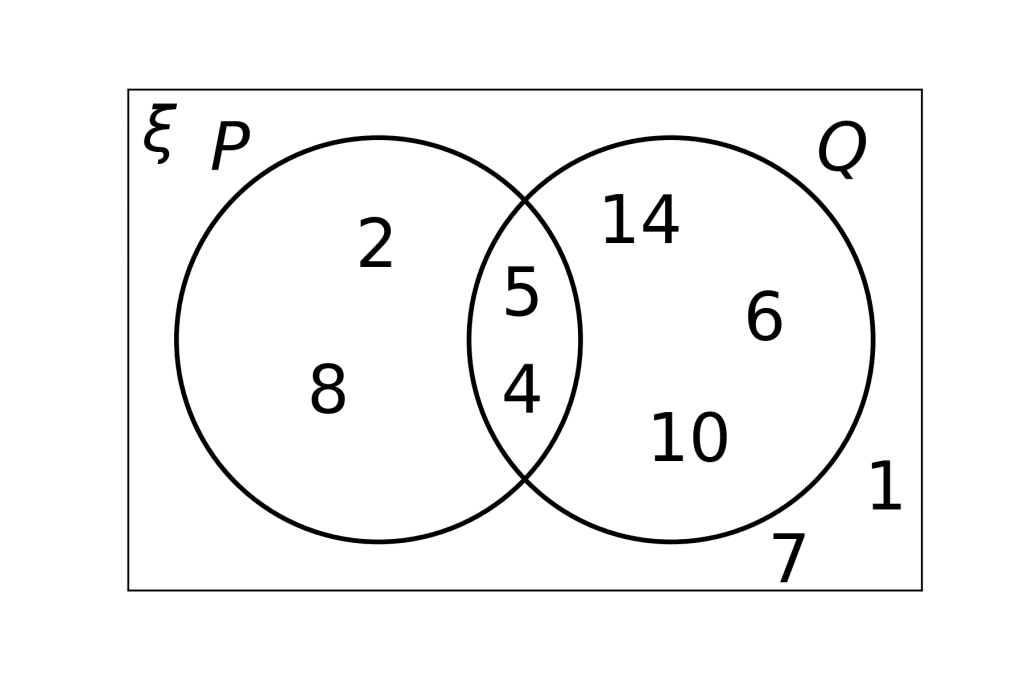

State which numbers are in the sets:
a) P \cap Q
b) Q’
c) P\cup Q
[3 marks]
a) P\cap Q means all elements that are in both P and Q. Looking at the Venn diagram, this must be where the circles intersect. So, we get
P\cap Q=\{4, 5\}
b) Q’ means all numbers not in Q. All the numbers inside the Q circle are: 10, 6, 14, 4, and 5 (the ones in the intersection count). The numbers not in there are
Q’=\{2, 8, 7, 1\}
c) P\cup Q means any numbers that appear in either P or Q. So, anything in either circle. We get
P\cup Q=\{2, 8, 4, 5, 10, 6, 14\}
Example 3: Sets and Inequalities
Solve the inequality 3x-7>11. Write your answer using set notation.
[2 marks]
We solve linear inequalities like we do linear equations. Adding 7 to both sides, we get
3x >7+11=18
Then, dividing both sides by 3, we get
x>6
Now, to express this in set notation, we want to put “x :” before it and put the whole thing in curly brackets:
\{x : x>6\}
Set Notation Example Questions
Question 1: \xi = \{103, 104, 105, 109, 110, 112, 114\}
A = \text{ even numbers} from \xi
B = \{103, 112, 114\}
State which numbers belong to the following:
a) A\cup B
b) A’
[2 marks]
a) The first thing we need to do is work out which numbers belong to the subset A. Since A is the subset consisting of even numbers, then the following numbers belong in subset A:
A=\{104, 110, 112, 114\}
The \cup symbol tells us that we need to combine subsets A and B, so when we combine the even numbers from subset A with the 3 numbers in subset B, we have the following numbers:
A\cup B=\{103, 104, 110, 112, 114\}
(Note that you don’t write the numbers 112 and 114 twice.)
b) The dash after the A means that we are interested in the set of numbers that are not in subset A.
Since we already know that A is the subset of even numbers, A' is the group of odd numbers from the universal set \xi:
A’=\{103, 105, 109\}
Question 2: \xi = \{1, 2, 3, 5, 7, 8, 9, 10, 12\}
V = \text{ prime numbers} in \xi
V\cap W = \{3, 5, 7\}
V\cup W = \{1, 2, 3, 5, 7, 10, 12\}
Fill in the Venn diagram below to display this information.
[4 marks]
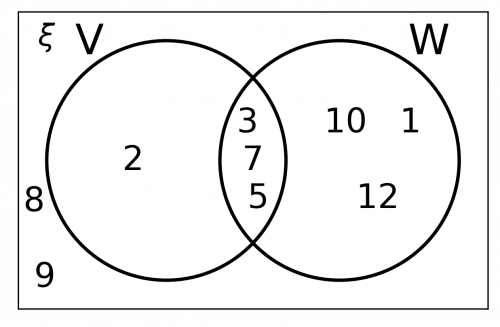
The first thing we need to do is work out which numbers from the universal set are in subset V, the set of prime numbers:
V = \{2, 3, 5, 7\}
(Remember that a prime number is a number which is only divisible by itself and 1.)
We are told in the question that V\cap W=\{3, 5, 7\}. This means 3, 5 and 7 are in both circles. This means that these numbers must be placed in the small area where the two circles overlap.
This means that the only remaining number from the subset V, the number 2, still needs to be placed. The number 2 needs to be placed inside the V circle, but outside the W circle (in other words, not in the intersection).
Now that we have organised all the elements of subset V, all the other numbers that are part of V\cup W need to be placed inside W, but outside V (again, not in the intersection). These values that we need to be place here are the numbers 1, 10, and 12.
Finally, there are still some numbers in the universal set \xi which have not yet been placed. All these numbers, the numbers 8 and 9, need to placed outside the circles, but still inside the rectangle.
Your completed Venn diagram should be similar to the below:
Question 3: Write the following inequalities using set notation.
a) x \geq 12
b) z < -2
c) a > 0
d) 13 < x
[4 marks]
The process for all 4 questions will be the same. Write the variable followed by a colon before the inequality, and then put everything inside curly brackets { }. The results are as follows:
a) \{x : x \geq 12\}
b) \{z : z < -2\}
c) \{a : a > 0\}
d) \{x : 13 < x\}
Question 4: Fill in the Venn diagram to show the following sets where \xi = {x : x is an integer, 1 < x < 21}
A = {x : x is a prime number}
B = {x : x is a factor of 24}
C = {x : x is a square number}
[5 marks]
The question may appear a little bit off-putting due to the set notation. The key facts we need to understand are that:
- the universal set (all the numbers in the set) must be greater than 1 (so from 2 onwards), but less than 21 (so up to and including 20).
- all the numbers in set A are prime numbers.
- all the numbers in set B are factors of 24 (numbers that 24 can be divided by).
- all the numbers in set C are square numbers.
It would probably be useful at this stage to write down which numbers fit into each set, and then see which numbers appear in multiple sets.
The prime numbers from 2 – 20 are: 2, \, 3, \, 5, \, 7, \, 11, \, 13, \, 17, \, 19. These are the numbers that will appear in set A.
The factors of 24 are: 2, \, 3, \, 4, \, 6, \, 8, \, 12. These are the numbers that will appear in set B.
The square numbers are: 4, 9 and 16. These are the numbers that will appear in set C. We can write these sets as:
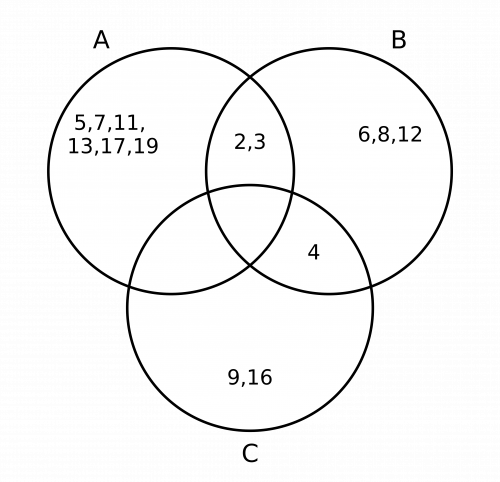
\begin{aligned} A&= \{2, \, 3, \, 5, \, 7, \, 11, \, 13, \, 17, \, 19\} \\ B&= \{2, \, 3, \, 4, \, 6, \, 8, \, 12\} \\ C &= \{4, \, 9, \, 16\}\end{aligned}
The first thing to check is to see if there are any numbers that belong to all three sets. There aren’t any, so the intersection of the three circles will be empty.
Having done this, look for any numbers that are common to 2 sets. Sets A and B share numbers 2 and 3, and sets B and C share the number 4. Therefore, we need to write 2 and 3 in the intersection of circle A and circle B, and the number 4 in the intersection of circle B and circle C.
In set A, we have already input numbers 2 and 3 on the Venn diagram, so we now need to input numbers 5, \, 7, \, 11, \, 13, \, 17, \, 19. These numbers should be placed in the A circle, but not in any of the intersections.
In set B, we have already input numbers 2, 3 and 4 on the Venn diagram, so we now need to input numbers 6, 8 and 12. These numbers should be placed in the B circle, but not in any of the intersections.
In set C, we have input the number 4 on the Venn diagram, so we now need to input numbers 9 and 16. These numbers should be placed in the C circle, but not in any of the intersections.
The completed Venn diagram should look like the below:
Question 5: Shade the region that represents (A'\cap B')
[1 mark]
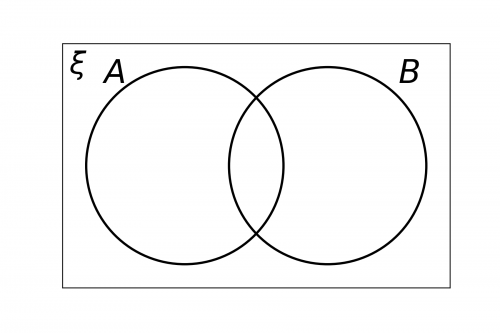
To work out the what area to shade, we need to be really clear on what (A'\cap B') means:
A' means everything ‘not in A‘.
B' means everything ‘not in B‘.
\cap means ‘the intersection of’.
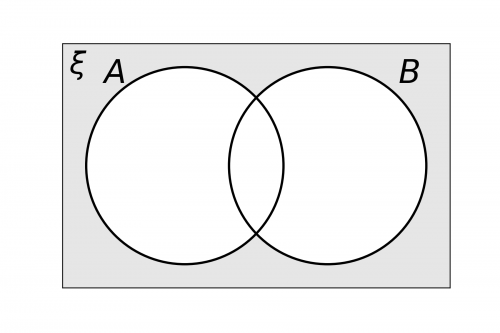 Therefore, we need to shade anything that is not in A and which is also not in B. Anything not in A and not in B is everything outside of the circles, so the Venn diagram should be shaded as follows:
Therefore, we need to shade anything that is not in A and which is also not in B. Anything not in A and not in B is everything outside of the circles, so the Venn diagram should be shaded as follows:
Set Notation Worksheet and Example Questions
(NEW) Set Notation Exam Style Questions - MME
Level 4-5GCSENewOfficial MME
MME Premium Membership
£19.99
/monthLearn an entire GCSE course for maths, English and science on the most comprehensive online learning platform. With revision explainer videos & notes, practice questions, topic tests and full mock exams for each topic on every course, it’s easy to Learn and Revise with the MME Learning Portal.
Sign Up Now






