Rounding Numbers
Rounding Numbers Revision
Rounding Numbers
Rounding is a process of simplifying a number without changing the value of it too much. We do this by taking a number and working out which of the “simpler” numbers it is closest to.
If you round numbers too early, i.e. during a calculation, then the answer you get at the end may be incorrect, so only round at the end of an answer, and not during a calculation, unless the question specifically asks you to.
Make sure you are happy with the following topics before continuing.
Skill 1: Rounding – Decimal Places
One way we may be asked to round a number is to a given number of decimal places (d.p.).
Example: Round 3.6874 to 2 decimal places.
Step 1: Determine the cut-off point.
Here, this is the 2nd decimal place. The cut-off point is after the 8 and before the 7.
Step 2: Look at the first digit after the cut-off point. Here it is the 7.
If it is below 5, then we keep the cut-off digit (i.e. the number before the cut-off point) the same.
If it is 5 or more, then we round up the cut-off digit.
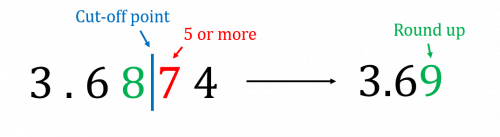
Here, 7 is more than 5, so we round the cut-off digit, 8, up to 9.
Step 3: All the digits after the cut-off point we ignore. So,
3.6874 rounded to 2 decimal places is 3.69
Skill 2: Rounding – Significant Figures
Another way we may be asked to round a number is to a given number of significant figures (sf). The 1st significant figure of a number is the first digit that isn’t a 0. The next significant figures immediately follows, and so on…..
Example: Round 0.04529 to 2 significant figures.
Step 1: Determine the cut-off point.
Here this is after the 2nd significant figure. The 1st significant figure is 4 as the first 2 digits are zeros.
The 2nd significant figure is the 5.
The cut-off point is between the 5 and the 2.
Step 2: Look at the first digit after the cut-off point. Here it is the 2.
If it is below 5, then we keep the cut-off digit the same.
If it is 5 or more, then we round up the cut-off digit.

Here, 2 is less than 5, so we keep the cut-off digit, 5, the same.
Step 3: All the digits after the cut-off point we ignore. So,
0.04529 rounded to 2 significant figures is 0.045
Skill 3: Rounding – Nearest Whole Number, 10, 100 etc.
Finally, we may be asked to round a number to the nearest whole number, 10, 100 etc.
This is easier than for decimal places and significant figures. We use the same method, but if it asks to round to the nearest 10 for example, then our cut-off digit will be the digit in the tens column.
Example: Round 112 to the nearest ten
Step 1: Identify the tens digit, here it will be the second 1
1\overset{\downarrow}{1}2
Step 2: Look at the digit after the tens column. Here it is 2
If it is below 5, then we keep the cut-off digit the same.
If it is 5 or more, then we round up the cut-off digit.
Here, 2 is less than 5 so we do not round up.
Step 3: All the digits after the cut-off digit we turn into 0‘s.
This gives the final answer to be:
110
Skill 4: Rounding – Carrying the 1
For each of the 3 ways of rounding, if we are required to round up a 9, then we round the 9 to a 0 and increase the digit before it by 1 (carry the 1 to the left).
Example: Round 4.398 to 2 decimal places.
The 2nd digit after the decimal point, the 9, is our cut-off digit. The digit after it is an 8, so we must round up the cut-off digit.
The problem is, increasing a 9 by 1 makes 10, so what do we do? The cut-off digit becomes zero, and the digit before it gets increased by 1. So, in this case, the 9 goes to zero and the 3 before it becomes 4.
Then, ignoring all the digits after the cut-off point, we get
4.398 rounded to 2 decimal places is 4.40
Example 1: Rounding to the Nearest 10
Round 235 to the nearest ten.
[1 mark]
The first digit, 2, is in hundreds, but the second digit, 3, is in tens, so that will be our cut-off digit.
Now we look to the digit after this: it is a 5, which means that we round up, i.e. the cut-off digit gets increased by 1, so in this case the 3 will become a 4.
Finally, turning all the digits after the cut-off point to 0 ‘s, we get that
235 rounded to the nearest 10 is 240
Example 2: Rounding Decimals
Round 13.746 to 2 decimal places.
[1 marks]
If we’re rounding to 2 decimal places, then the cut-off digit is before the 2nd decimal place, i.e. the 2nd number after the decimal point. In this case, that is the 4.
The digit after the 4 is a 6, which means that we round up and increase the cut-off digit by 1 so the 4 becomes a 5, giving us
13.746 rounded to 2 decimal places is 13.75
Example 3: Rounding Significant Figures
Round 8,529 to 2 significant figures.
[1 mark]
The 1st significant figure is 8, the 2nd is 5.
The 5 is our cut-off digit.
The digit after the 5 is a 2. This is less than 5, so we round down and the cut-off digit stays the same.
Then, turning all the digits after the cut-off digit into 0‘s, we get
8,529 rounded to 2 significant figures is 8,500
Example 4: Rounding Significant Figures
Round 0.00589 to 2 significant figures.
[1 mark]
The first non-zero term is 5, so this is our \, 1st significant figure. 8, is our 2nd significant figure and thus is our cut-off digit.
The digit after the 8 is a 9, which is bigger than 5, and so we round up, increasing the cut-off digit by 1, making the 8 into a 9.
Then, ignoring all the digits after the cut-off point, we get
0.00589 rounded to 2 significant figures is 0.0059
Rounding Numbers Example Questions
Question 1: Round 560,180 to the nearest thousand.
[1 mark]
Here, we are rounding to the nearest thousand so it is the 3rd digit we are interested in,
560,180
To round up or down we have to consider the value of the digit to its immediate right which in this case is 1.
As 1 is less than 5, we round down and so the zero stays the same and we make the rest of the digits zero,
560,180 rounded to the nearest thousand is 560,000
Question 2: Round 97.96 to 1 decimal place.
[1 mark]
Here, we are rounding to 1 decimal place so it is the 1st digit after the decimal point we are interested in,
97.96
To round up or down we have to consider the value of the digit to its immediate right which in this case is 6.
As 6 is greater than 5, we round up. However, as we are rounding up 9 to 10, we have to carry the 1 over to the units column, so we get,
97.96 rounded to 1 decimal place is 98.0
Question 3: Round 0.02345 to 3 significant figures.
[1 mark]
Here, we are rounding to 3 significant figures so it is the first non-zero digit and the two digits that follow it that we are interested in,
0.02345
The 1st significant figure in this case is 2 and moving two places along we see that the 4 is the 3rd significant figure. To round up or down we have to consider the value of the digit to its immediate right which in this case is 5, so we round up,
0.02345 rounded to 3 significant figures is 0.0235
Question 4: Round 1.0093 to 3 significant figures.
[1 mark]
Here, we are rounding to 3 significant figures so it is the first non-zero digit and the two digits that follow it that we are interested in,
1.0093
The 1st significant figure in this case is 1 and moving two places along we see that the 0 is the 3rd significant figure. To round up or down we have to consider the value of the digit to its immediate right which in this case is 9, so we round up,
1.0093 rounded to 3 significant figures is 1.01
Question 5: Round 55.099 to 2 decimal places.
[1 mark]
Here, we are rounding to 2 decimal places so it is the 2nd digit after the decimal point we are interested in,
55.099
To round up or down we have to consider the value of the digit to its immediate right which in this case is 9. As 9 is greater than 5, we round up. However, as we are rounding up 9 to 10, we have to carry the 1 over to the units column, so we get,
55.099 rounded to 2 decimal places is 55.10






