Revise
Place Value
Place Value Revision
Place Value
Place value is all about the value of each digit within a number. Each digit has a different value determined by its position.
Make sure you are happy with the following topics before continuing.
Place Value: Large Numbers
Going from left to right, the value of each digit decreases.
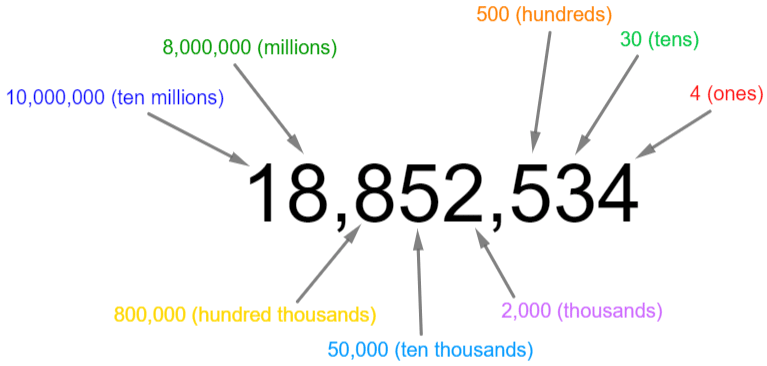
Note: A quick way to state how much a digit is worth is simply to make all the other digits in the number into zeros. This works the same way for decimal place value, as we are about to see.
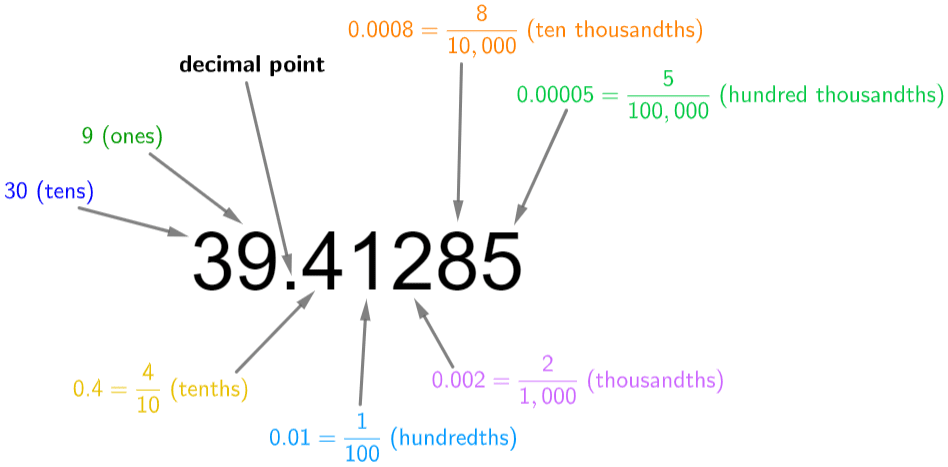
Place Value: Decimals
A decimal is any number with a decimal point. They are the numbers that fall between the integers.
Digits after the decimal place also have a value, but this decreases the further you move away (to the right) from the decimal point.
Example 1: Large Number
State the place value of the 6 in 4,609.
[1 mark]
Counting from right to left, we can see that the 6 is in the third column along – the hundreds column. Therefore, the value of the ‘6 digit’ in this number is 600.
Example 2: Decimals
In the number 0.56023, what is
a) The value of the 5?
b) The value of the 2?
[2 marks]
a) The 5 is the first digit after the decimal place, meaning it is in the tenths column. So, it is worth
\dfrac{5}{10} or 0.5
b) The 2 is the 4th digit after the decimal place, meaning it is in the ten thousandths column. So, it is worth
\dfrac{2}{10,000} or 0.0002
Note: In both of these cases, the trick of “making all other digits into zeros” would give us the correct answer.
Place Value Example Questions
Question 1: In the number 1,899, what is the value of the 8?
[1 mark]
The 8 is the 3rd digit from the right, meaning it’s in the hundreds column. So, the value is,
800 or \text{eight hundred}
Question 2: In the number 32.107, what is the value of the 1?
[1 mark]
The 1 is one place after the decimal point, meaning it is in the tenths column. So, the value is,
\dfrac{1}{10} or \text{one tenth}
Question 3: In the number 0.0461, what is the value of the 6?
[1 mark]
The 6 is three places after the decimal point, meaning it is in the thousandths column. So, the value is
\dfrac{6}{1000} or \text{six thousdandths}
Question 4: In the number 549,023, what is the value of the 5?
[1 mark]
The 5 is the 6th digit from the right, meaning it’s in the hundred thousands column. So, the value is,
500,000 or \text{five hundred thousand}
Question 5: Becky is thinking of a number. Her number has 3 thousands, 5 tens, and 1 hundredth. What is her number?
[2 marks]
3 thousands = 3,000
5 tens = 50
1 hundredth = 0.01
Adding these all together, we get Becky’s number to be
3,000+50+0.01=3,050.01
