Quadratic Sequences

GCSELevel 6-7AQAEdexcelOCRWJEC

Quadratic Sequences Revision

Quadratic Sequences

A quadratic sequence is a sequence whose $n^{th}$ term formula is a quadratic i.e. it has an $n^2$ term, so takes the form,

$\textcolor{red}{a}n^2+\textcolor{blue}{b}n+\textcolor{limegreen}{c}$ ,

where $a, b,$ and $c$ are all numbers. The resulting sequences don’t have a common difference between each term as linear sequences do, but rather the difference between the differences remains the same.

Make sure you are happy with the following topics before continuing

Finding the $n^{th}$ Term of a Quadratic Sequence ( $a=1$ )

Example: Find the $n^{th}$ term formula of the following quadratic sequence.

$2, 9, 18, 29, 42.$

Step 1: Find the difference between each term, and find the second differences (i.e. the differences between the differences);

To do this, we will first find the differences between the terms in the sequence.

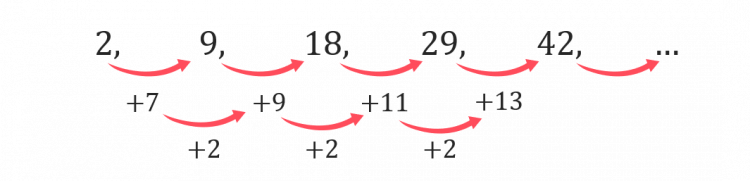
Quadratic Sequence Example Finding 2nd Common Difference

We can see that unlike a linear sequence, the differences aren’t the same. However, if we then look at the differences between those differences, we see the second differences are the same.

We now know the $n^{th}$ term formula is $\textcolor{red}{a}n^2+\textcolor{blue}{b}n+\textcolor{limegreen}{c}$ .

To find the value of $\textcolor{red}{a}$ we find the second difference, which is $2$ , and divide this by $2$ . Hence $\textcolor{red}{a=1}$ .

Step 2: Subtract $\textcolor{red}{a}n^2$ from the original sequence.

We still need to find $\textcolor{blue}{b}$ and $\textcolor{limegreen}{c}$ . To do this we substitute the values of $n$ from $1$ to $5$ into $\textcolor{red}{a}n^2$ , and write the results below the original sequence as shown.

Quadratic Sequence Table Of Values

$u_n =$ the original sequence.

If you look carefully at $u_n - n^2$ you will notice it is a linear sequence whose $n^{th}$ term will give us the missing letters of the quadratic $n^{th}$ term that we want.

Step 3: Find the $n^{th}$ term of the new linear sequence.

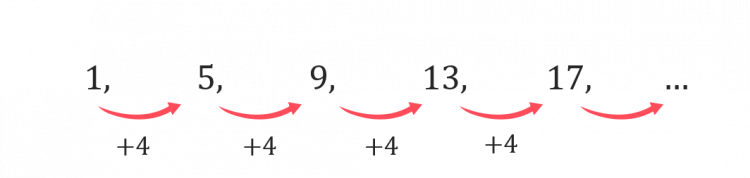
New Linear Sequence From Quadratic Sequence u_n-n^2 Find an+b

The $n^{th}$ term for this linear sequence is $4n-3$ .

Step 4: Write the final $n^{th}$ term for the full quadratic sequence.

This formula is precisely the last part of the quadratic $n^{th}$ term formula that we set out to find in the first place. Hence we get our final $n{th}$ term to be,

$n^2+4n-3$ .

Finding the $n^{th}$ Term of a Quadratic Sequence ( $a\gt1$ )

Example: Find the $n^{th}$ term formula of the following quadratic sequence.

$4, 15, 32, 55, 84$

Step 1: Find the difference between each term, and find the second differences (i.e. the differences between the differences);

We will first find the differences between the terms in the sequence.

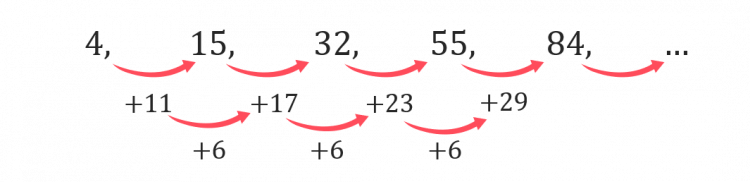
Second Difference Quadratic Sequence Find n^2 coefficient a

To find the value of $a$ we find the second difference, which is $6$ , and divide this by $2$ . Hence $a=3$ .

Step 2: Subtract $\textcolor{red}{3}n^2$

We still need to find $\textcolor{blue}{b}$ and $\textcolor{limegreen}{c}$ . To do this we substitute the values of $3n^2$ from $1$ to $5$ into this, and write the results below the original sequence as shown.

Quadratic Sequence Table Of Values New Linear Sequence

$u_n =$ the original sequence

Here, we have subtracted our values for $3n^2$ from the actual sequence to form a linear sequence, the $n^{th}$ term of which will give us the missing letters of the quadratic $n^{th}$ term that we want.

Step 3: Find the $n^{th}$ term of the new sequence.

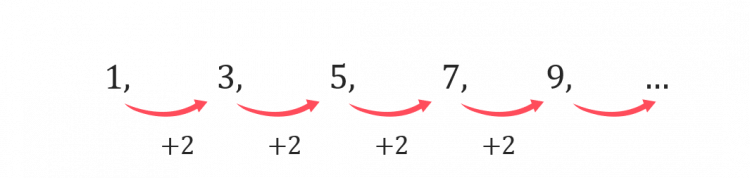
New Linear Sequence From Quadratic Sequence Find n And Constant Coefficient an+b

The $n^{th}$ term for this linear sequence is $u_n=2n-1$ .

Step 4: Write the final $n^{th}$ term for the full quadratic sequence.

This formula is precisely the last part of the quadratic $n^{th}$ term formula that we set out to find in the first place. Hence we get our final $n^{th}$ term to be,

$u_n=3n^2+2n-1$ .

Summary of Steps to find the $n^{th}$ Term

Every time you need to find the $n^{th}$ term formula for a quadratic sequence, the method is the same.

To find $\textcolor{red}{a}n^2+\textcolor{blue}{b}n+\textcolor{green}c$ , the steps are:

Find the difference between each term, and find the second differences (i.e. the differences between the differences);
Check that the second differences are all the same, and then halve that number to get $\textcolor{red}{a}$ ;
Write out the terms of the sequence again, then substitute the first few values of $n$ into $an^2$ and write the results below the original sequence.
Subtract the elements of the second row from the elements above them in the first row.
Treat these differences like a sequence and find the $n^{th}$ term of that linear sequence.
Finally, combine the $\textcolor{red}{a}n^2$ that you found in step 2 with the $\textcolor{blue}{b}n+\textcolor{green}{c}$ that you found in step 5, and you’ve got your quadratic $n^{th}$ term formula.

Note:

Subscript notation can be used to denote position to term and term to term rules.

For example

$x_{n+1}=x_n^2+5x-1$ shows that you square the previous term, add $5$ times the previous term and subtract $1$ to get the next term.

$y_n=4n^2-5n+3$ gives you a rule for the $n$ th term of a sequence.

Quadratic Sequences Example Questions

Question 1: A sequence has the $n^{th}$ term $n^2+6n -10$

List the first $5$ terms in this sequence.

[1 mark]

To generate the first $5$ terms of this sequence, we will substitute $n=1, 2, 3, 4, 5$ into the formula given.

$\begin{aligned}n=1 \text{ gives } &(1)^2+6(1)-10=-3 \\n=2 \text{ gives } &(2)^2+6(2)-10=6 \\ n=3\text{ gives } &(3)^2+6(3)-10=17 \\ n=4 \text{ gives } &(4)^2+6(4)-10=30 \\ n=5 \text{ gives } &(5)^2+6(5)-10=45\end{aligned}$

Hence the first five terms of the sequence are,

$-3, 6, 17, 30, 45$

Save your answers with

Gold Standard Education

Question 2: A sequence has the $n^{th}$ term $n^2-2$

a) Find the first $4$ terms in this sequence.

[2 marks]

b) A term in this sequence is $287$ . Find the position of this term in the sequence.

[2 marks]

a) To generate the first $4$ terms of this sequence, we will substitute $n=1, 2, 3, 4$ into the formula given.

$\begin{aligned}n=1 \text{ gives } &(1)^2-2 =-1 \\ n=2 \text{ gives } &(2)^2-2 =4 \\ n=3 \text{ gives } &(3)^2-2=7 \\ n=4 \text{ gives } &(4)^2-2=14 \end{aligned}$

b) Every term in this sequence is generated when an integer value of $n$ is substituted into $n^2-2$

Hence if we set $287$ to equal $n^2-2$ , we can determine its position in the sequence,

$n^2-2=287$

making $n$ the subject,

$n=\sqrt{287+2}=17$

Hence $287$ is the $17^{th}$ term in the sequence.

Save your answers with

Gold Standard Education

Question 3: A sequence has the $n^{th}$ term $(n-1)^2$

A term in this sequence is $49$ . Find the position of this term in the sequence.

[2 marks]

Every term in this sequence is generated when an integer value of $n$ is substituted into $(n-1)^2$

Thus if we set $49$ to equal $(n-1)^2$ , we can determine its position in the sequence,

$\begin{aligned}(n-1)^2&=49 \\ n-1 &=\pm\sqrt{49} \\ n&=1 +7 = 8\end{aligned}$

Hence $49$ is the $8^{th}$ term in the sequence, as $n$ can only be positive integers.

Save your answers with

Gold Standard Education

Question 4: Find the $n^{th}$ term formula for the following quadratic sequence,

$9, 20, 33, 48, 65$

[5 marks]

So, the $n^{th}$ term formula will take the form $an^2+bn+c$ where $a, b,$ and $c$ are numbers to be determined.

Firstly, we have to find the differences between the terms in the sequences, and then find the difference between the differences. Doing so, we find,

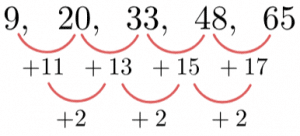
The second difference is the same, as expected, therefore $a$ is half of the second difference and so $a=1$

Now we need to find $b$ and $c$ by comparing the values generated by a sequence of $n^2$ , to the original sequence.

$\begin{aligned} u_n &= 9 , 20, 33, 48, 65 \\ n^2 &= 1, 4, 9, 16, 25 \\ u_n - n^2 &= 8, 16, 24, 32, 40\end{aligned}$

The difference, is a linear sequence whose $n^{th}$ term formula is precisely $bn+c$ , so

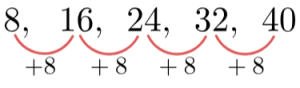
The difference is $8$ , so the $n^{th}$ term must be $8n+c$ where $c=0$

Therefore, we get the $n^{th}$ term formula of the quadratic to be,

$n^2+8n$

Save your answers with

Gold Standard Education

Question 5: Find the $n^{th}$ term formula for the following quadratic sequence,

$0, 1, 6, 15, 28$

[5 marks]

So, the $n^{th}$ term formula will take the form $an^2+bn+c$ where $a, b,$ and $c$ are numbers to be determined.

Firstly, we have to find the differences between the terms in the sequences, and then find the difference between the differences. Doing so, we find,

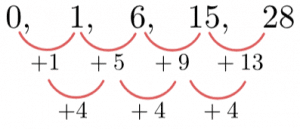
The second difference is the same, as expected, therefore $a$ is half of the second difference and so $a=2$

Now we need to find $b$ and $c$ by comparing the values generated by a sequence of $2n^2$ , to the original sequence.

$\begin{aligned}u_n & = 0, 1, 6, 15, 28 \\ 2n^2 & = 2, 8, 18, 32, 50 \\u_n-2n^2 & = -2, -7, -12, -17, -22\end{aligned}$

The difference, is a linear sequence whose $n^{th}$ term formula is precisely $bn+c$ , so

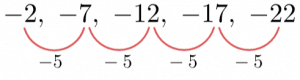
The difference is $-5$ , so the $n^{th}$ term must be $-5n+c$ . Then, for $n=1$ , we get $-5n=-5$ , whereas the first term is not $-5$ , but $-2$ . To get from $-5$ to $-2$ we have to add $3$ , so we must have that $c=3$ , and thus the $n^{th}$ term is