Prime Factors LCM HCF
Prime Factors LCM HCF Revision
Prime Factors, HCF and LCM
Understanding prime factors is important to be able to find the Lowest Common Multiple (LCM) and Highest Common Factor (HCF) of two or more numbers. Make sure you are happy with the following topics before continuing.
Prime Factorisation and Factor Trees
We define a prime factor of any given number to be any factor that the number has, that is also a prime number.
Every positive whole number has a unique prime factorisation – a list of prime numbers that, when multiplied together, give you the original number. In more complicated cases, we use something called a factor tree.
Example: Determine the prime factorisation of 60.
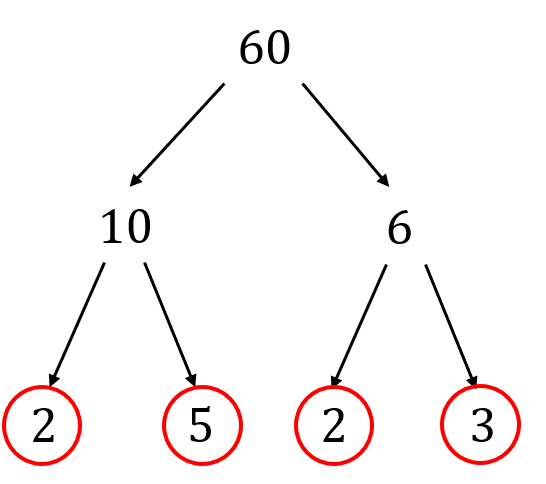

Step 1: To construct a factor tree, think of 2 numbers which multiply together to make 60 – here, we’ve gone with 10 and 6.
Step 2: Draw two branches coming down from 60, and at the end of the branches write the two factors that you chose.
Step 3: If a factor is prime, then circle it. If a factor is not prime, then repeat the process as shown in the factor tree below.
Step 4: The prime factorisation of 60 is therefore
60 = 2 \times 2 \times 3 \times 5
Step 5: We write this prime factorisation in index form, where if there is more than one of the same factor, we write it as a power instead, where the power is the number of times it occurs. So
60= 2^2 \times 3\times 5
Highest Common Factor – HCF
The Highest Common Factor, or HCF, of two numbers is the biggest number that goes into both of them.
Example: Consider the numbers 12 and 20
The factors of 12 are: 1, 2, 3, 4, 6, and 12
The factors of 20 are: 1, 2, 4, 5, 10, and 20
They have a few factors in common, but the biggest factor they have in common is 4, therefore 4 is the HCF of 12 and 20.
Lowest Common Multiple – LCM
The lowest common multiple, or LCM, of two numbers is the smallest number that is a multiple of both of them.
Example: Consider the numbers 5 and 7
Multiples of 5 are: 5, 10, 15, 20, 25, 30, 35, 40, 45, …
Multiples of 7 are: 7, 14, 21, 28, 35, 42, … and so on.
So, we can see that the first occurrence of a number which is a multiple of both of these numbers is 35, therefore 35 is the LCM of 5 and 7.
HCF and LCM – Venn Diagrams
For large numbers, the easiest way to find the HCF and LCM is to use Venn diagrams.
Example: Find the HCF and LCM of 60 and 27.
Step 1: We first need the prime factorisation of both numbers, in which we would use factor trees. However we already have the prime factorisation of 60, which is
60 = 2 \times 2 \times 3 \times 5 = 2^2 \times 3 \times 5 and 27= 3 \times 3 \times 3 = 3^3
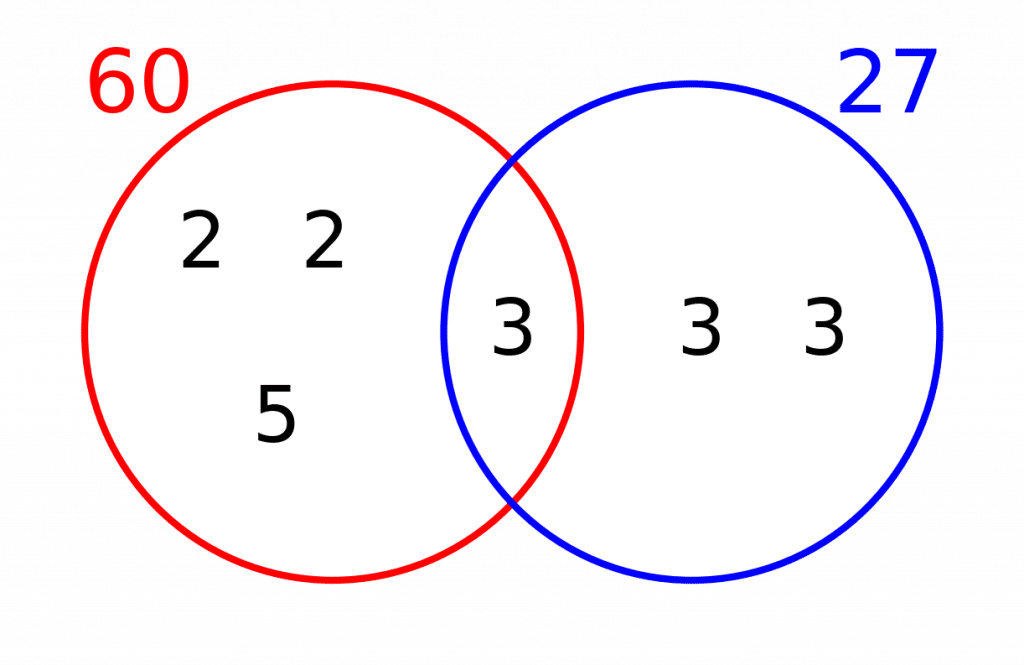

Step 2: Now, we draw a Venn diagram where one circle is for prime factors of 60 and one circle is for prime factors of 27.
Step 3: Looking at the list of factors, if one is shared by both numbers, then we will put it in the intersection and cross it off both lists.
\textcolor{red}{60} = 2 \times 2 \times \bcancel{3} \times 5 and \textcolor{blue}{ 27} = \bcancel{3} \times 3 \times 3
Step 4: Any factors that are not shared and haven’t been crossed out, we put in their respective circles.
Step 5: To find the HCF, we multiply the numbers in the intersection (these are the factors that are common between both numbers). Here there is only one number, so
HCF = 3
Step 6: To find the LCM, we multiply all of the numbers in the Venn diagram together. So
LCM = 2 \times 2 \times 5 \times 3 \times 3 \times 3
Example: Prime Factor Tree
Find the LCM and HCF of 420 and 132.
[4 marks]
To do this method, we require the full prime factorisation of both 420 and 132. So, we’re going to use the factor tree method.
The prime factor tree for 420 can be seen on the right,
This gives,
2\times2\times3\times 5\times 7 = 2^2 \times 3 \times 5 \times 7
Going through the same process, we get that the full prime factorisation of 132 is
2\times2\times 3\times 11 = 2^2 \times 3 \times 11

So, now that we have the prime factorisation, we need to draw a Venn diagram where one circle is for prime factors of 420 and one circle is for prime factors of 132.
Looking at the lists of factors, if one is shared by both numbers, then we will put it in the intersection and cross it off both lists.
Then, any factors that aren’t shared, and so haven’t been crossed out, will be put in their respective circles.
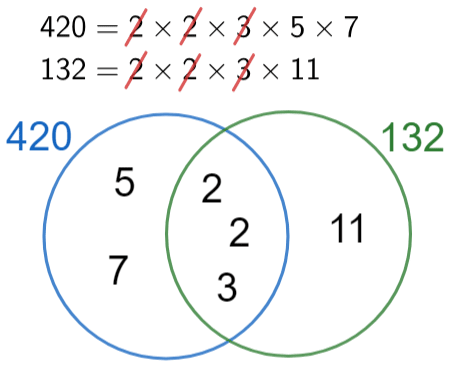

To find the HCF is to multiply the numbers in the intersection:
HCF =2\times2\times3=12
To find the LCM, all we need to do is multiply all the numbers now in the Venn diagram together:
LCM =5\times7\times2\times 2\times3\times11=4620
Prime Factors LCM HCF Example Questions
Question 1: Find the unique prime factorisation of 72.
Write your answer using index notation.
[2 marks]
The prime factors of a number can be displayed using a prime factor tree.
The prime factorisation of 72 is,
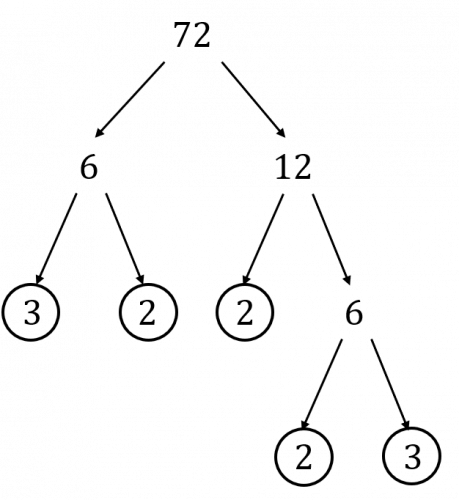
72=2\times2\times2\times3\times3
Written in index notation, the answer is,
72=2^3\times3^2
Question 2: Find the prime factorisation of 140.
Write your answer using index notation.
[2 marks]
The prime factors of a number can be displayed using a prime factor tree.
The prime factorisation of 140 is,
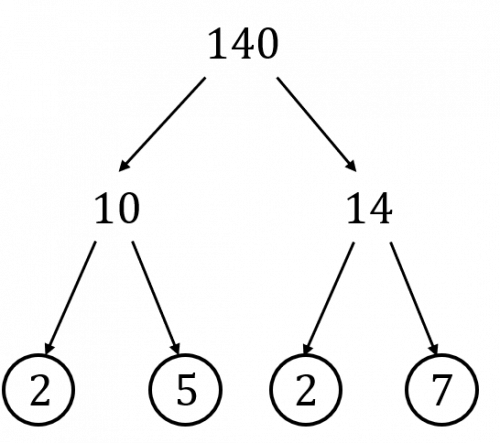
140=2\times2\times5\times7
Written in index notation, the answer is,
140=2^2\times5\times7
Question 3: Find the HCF and LCM of 24 and 40.
[4 marks]
First, we have to find the prime factorisation of 24 and of 40:
Prime factors of 24: 2\times2\times2\times3
Prime factors of 40: 2\times2\times2\times5
To find the HCF, find any prime factors that are in common between both numbers.
HCF = 2\times2\times2=8
Next, cross any numbers used so far off from the products.
Prime factors of 24: \cancel{2}\times\cancel{2}\times\cancel{2}\times3
Prime factors of 40: \cancel{2}\times\cancel{2}\times\cancel{2}\times5
To find the LCM, multiply the HCF by all the factors that have not been crossed out so far.
LCM = 8\times3\times5=120
Question 4: Find the HCF and LCM of 495 and 220.
[4 marks]
The prime factors of both 495 and 220 can be displayed using prime factor trees.
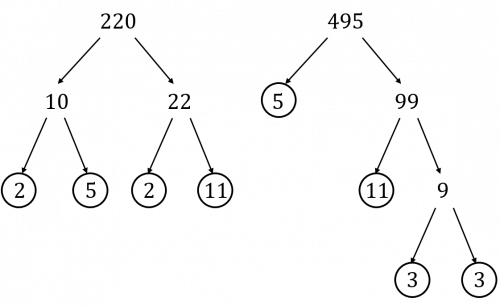
So, the factorisation of 220 is,
220=2\times2\times5\times11
and the factorisation of 495 is,
495=3\times3\times5\times11
Now, we will draw a Venn diagram with one circle containing the factors of 495 and the other containing the factors of 220. Any prime factors shared by these two numbers are to be placed in the intersection.
495=3\times3\times\cancel5\times\cancel11
220=2\times2\times\cancel5\times\cancel11
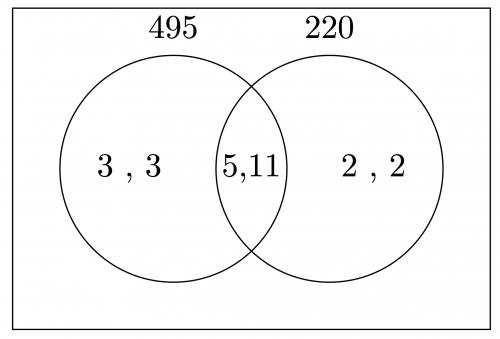
The HCF can be calculated by multiplying the numbers in the intersection together,
\text{HCF }=5\times11=55
Finally, we find the LCM by multiplying all the numbers in the Venn diagram together,
\text{LCM }=3\times3\times5\times11\times2\times2=1,980
Question 5: Find the HCF and LCM of 32, 152 and 600.
[5 marks]
First, we have to find the prime factorisation of 32, 152 and of 600:
Prime factors of 32=2\times2\times2\times2\times2
Prime factors of 152= 2\times2\times2\times19
Prime factors of 600= 2\times2\times2\times3\times5\times5
Then we can place each prime factor in the correct circle in the Venn diagram. Any common factors should be placed in the intersections of the circles.
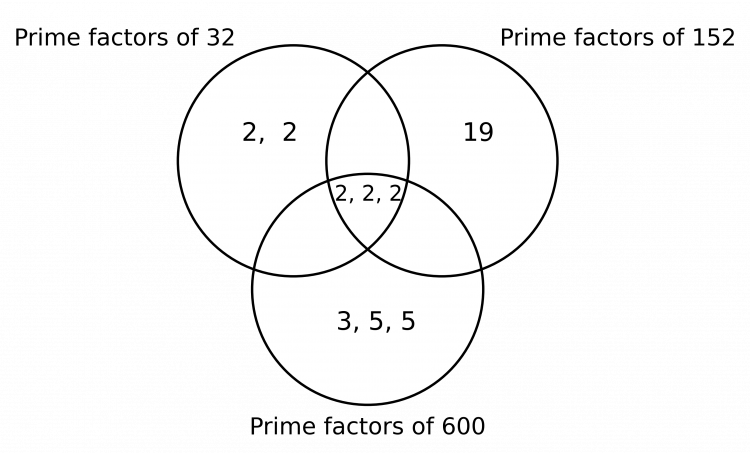
The highest common factor (HCF) is found by multiplying together the numbers in the intersection of all three of the circles.
HCF = 2\times2\times2=8
The lowest common multiple (LCM) is found by multiplying together the numbers from all sections of the circles.
LCM = 2\times2\times2\times2\times2\times3\times5\times5\times19=45600






