Pressure Force Area
Pressure Force Area Revision
Pressure Force Area
Pressure is a measure of how much force is applied over a given area of an object, so it is calculated by dividing the amount of force being applied by the area over which it is being applied.
Make sure you are happy with the following topics before continuing.
Pressure Force Area – Formula
Pressure, force and area are all related by the formula:
p = \dfrac{F}{A}
where p is the pressure, F is force, and A is area. You can rearrange this formula to find the other two, for example, if we multiply both sides of the equation by A, then swap the left-hand side and right-hand side, we get.
F = p \times A
So, we we can calculate the force by multiplying the pressure by the area.
Since area is measured in square metres (m^2), and force is measured in Newtons (N), the standard units for pressure are Newtons per square metre (N/m^2). These are compound units (for more information, see Conversions revision).
Pressure Force Area – Formula Triangle
A quick way of remembering how to calculate one of either pressure, force or area using the other two is to use the triangles below.
The horizontal line means divide and the \times symbol means multiply. We then:
We then cover up the one we want to find (represented by a red circle) and substitute values into the formula for the two remaining quantities in the triangle.
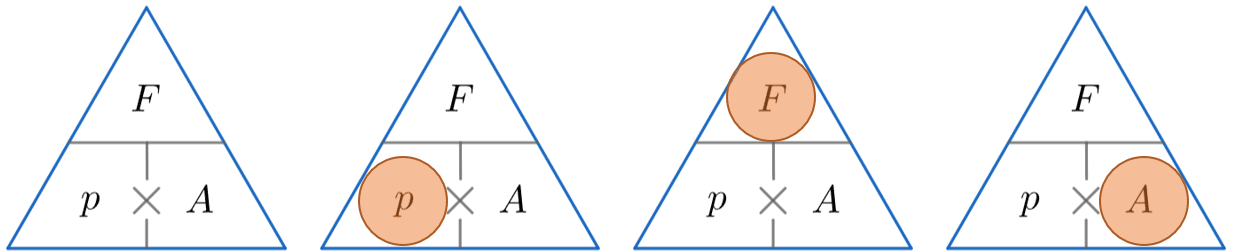
p = \dfrac{F}{A} \,\,\,\,\,\,\, \,\,\,\,\,\,\,\,\,\, F = p\times A\,\,\,\,\,\,\,\,\, \,\,\,\,\,\,\,\,\, A = \dfrac{F}{p}
Example 1: Calculating Pressure
A force of 150 N is being applied over an area measuring 0.5 m^2. Calculate the pressure on the object ensuring you give the correct units.
[2 marks]
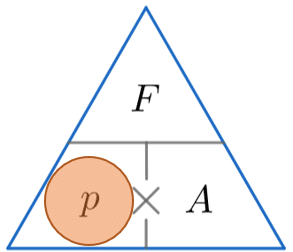

We’re looking for pressure, so constructing the triangle and covering up the p, we must divide the force by the area. So
\text{Pressure } = 150 \div 0.5 = 300 N/m^2
Example 2: Calculating Force
A woman is applying 300 N/m^2 of pressure onto a door with her hand. Her hand has area 0.02 m^2. Work out the force being applied.
[2 marks]
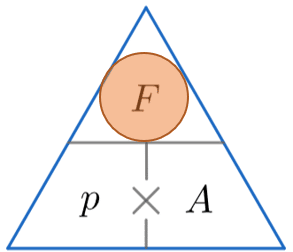

We’re looking for force, so constructing the triangle and covering up the F, we must multiply the pressure by the area. So
\text{Force } = 300 \times 0.02 = 6 N
Example 3: Calculating Area
Pressure of 150 N/m^2 is experienced when a force of 2 kN is applied. Calculate the area over which the force is applied to obtain the pressure stated.
[2 marks]
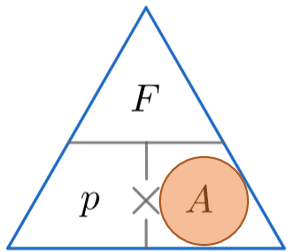

Now, before we do any calculations, we need to make sure our units are in the same form. In this example we need to convert kilo-newtons into newtons by multiplying by 1000. This gives us 2000 N.
We’re looking for area, so constructing the triangle and covering up the A, we must divide the force by the pressure. So
\text{Area } = 2000 \div 150 = 13.3 m^2
Pressure Force Area Example Questions
Question 1: A force of 185.6 N is applied to a square of side length 3 m. Work out the pressure on the square to 3 significant figures.
[2 marks]
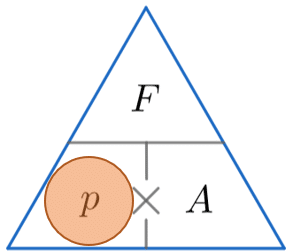
We are calculating the pressure, so by covering up p, we can see from the triangle above that we have to divide F by A.
Before we can do this calculation however, we need to work out the area of the square. Since the square has a side length of 3 m, the area can be calculated as follows:
3 m \times \, 3 m = 9 m^2
Now that we have the area and the force, we can calculate the pressure by substituting the values for the area and the force into the pressure equation as follows:
\text{pressure }=\dfrac{F}{A}=\dfrac{185.6}{9}=20.6222...=20.6 N/m^2 (3 sf).
The units must be N/m^2 since the units used in the question are N and m^2.
Question 2: A man with a weight of 740 N is standing on one leg. His foot is exerting 2312.5 N/m^2 of pressure onto the ground. What is the surface area of the bottom of his foot?
[2 marks]
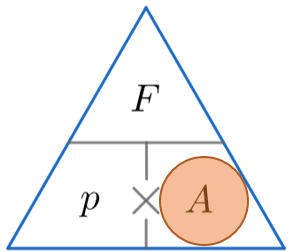
We are calculating the area, so by covering up A, we can see from the triangle above that we have to divide F by p. So, by substituting the known values for the force and the pressure into the equation, we can calculate the area as follows:
\text{Area }=\dfrac{F}{p}=\dfrac{740}{2312.5}=0.32latex] m[latex]^2
The unit must be m^2 since the units used in the question are N/m^2.
Question 3: A shipping container is removed from a ship and placed on the ground. The area of the container in contact with the ground is 16 m^2. The pressure exerted on the floor is 2480 N/m^2.
What force is being exerted by the shipping container on the ground?
[2 marks]
In this question, we are calculating the force, so we will need to rearrange the pressure / force / area equation.
Since
\text{pressure = force} \div \text{ area}
then
\text{force = pressure} \times \text{ area}
By substituting the values for the pressure and the area into the formula above, we can calculate the force as follows:
\text{Force } = 16 m^2 \times \, 2480 N/m^2 = 39,680 N
Question 4: A cylinder is resting on one of its circular faces on the ground. The weight of the cylinder is 4872 N and the cylinder exerts a pressure of 812 N/m^2 on the ground.
To 2 decimal places, what is the diameter of the cylinder?
[4 marks]
This may seem like an impossible question without sufficient information to go by at first glance. We have been given the pressure as well as the weight (force) of the cylinder. Since we know both the force and the pressure, the only thing we are able to calculate at this stage is the area of the circular cylinder face.
Since
\text{pressure = force} \div \text{ area}
then
\text{area = force} \div \text{ pressure}
By substituting the values for the force and the pressure into the formula above, we can calculate the area as follows:
4872 N \div \, 812 N/m^2 = 6 m^2
We now know that the area of the circular face on which the cylinder is resting has an area of 6 m^2, and from this information we need to work out the diameter of the cylinder / circle. In this question, we therefore need to apply some basic knowledge about the circle areas.
The formula for the area of a circle is \pi r².
However, we know the area and want a formula for the radius, so we will need to rearrange this formula.
First of all, we can both sides by \pi:
\dfrac{a}{π} = r^2
If we now take the square root of both sides, we have a formula for the radius:
\sqrt \dfrac{a}{π} = r
Since we know the area, all we need to do is divide the area by \pi, and square root the answer.
6 \div \pi = 1.9099
\sqrt {1.9099} = 1.38 m
If the radius of the circle is 1.38m, then the diameter will be double this:
\text{Diameter} = 2 \times 1.38 = 2.76 m
Question 5: A cube and a square-based pyramid exert the same pressure on the ground.
The square of the pyramid’s base has a side length of 8 metres and has a weight of 440 N. The cube has a weight of 110 N. What is the side length of the cube?
[4 marks]
This is another of these questions that might seem impossible initially, but there is sufficient information in the question to solve it. Like many maths problems, if you don’t have a clear strategy, just do any calculations you can, as they may lead somewhere useful!
Pressure Force Area Worksheet and Example Questions
(NEW) Pressure Force Area Exam Style Questions - MME
Level 4-5GCSENewOfficial MMEPressure Force Area Drill Questions
Density and Pressure - Drill Questions
Level 4-5GCSE
MME Premium Membership
£19.99
/monthLearn an entire GCSE course for maths, English and science on the most comprehensive online learning platform. With revision explainer videos & notes, practice questions, topic tests and full mock exams for each topic on every course, it’s easy to Learn and Revise with the MME Learning Portal.
Sign Up Now



