Parallel and Perpendicular Lines Questions and Revision

Parallel and Perpendicular Lines

Parallel Lines – are always the same distance apart and never meet (they have the same gradient).

Perpendicular Lines – meet at a right angle (the gradients of perpendicular lines multiply to $-1$ ).

Before continuing this topic, recap the following:

Parallel Lines – Same Gradient

Parallel lines have the same gradient.

Equation of a straight line: $y=\textcolor{#10a6f3}{m}x+c$

$\textcolor{#10a6f3}{m} \rightarrow$ gradient

$c \rightarrow y-$ intercept

For lines to be parallel, the value of $\textcolor{#10a6f3}{m}$ must be the same.

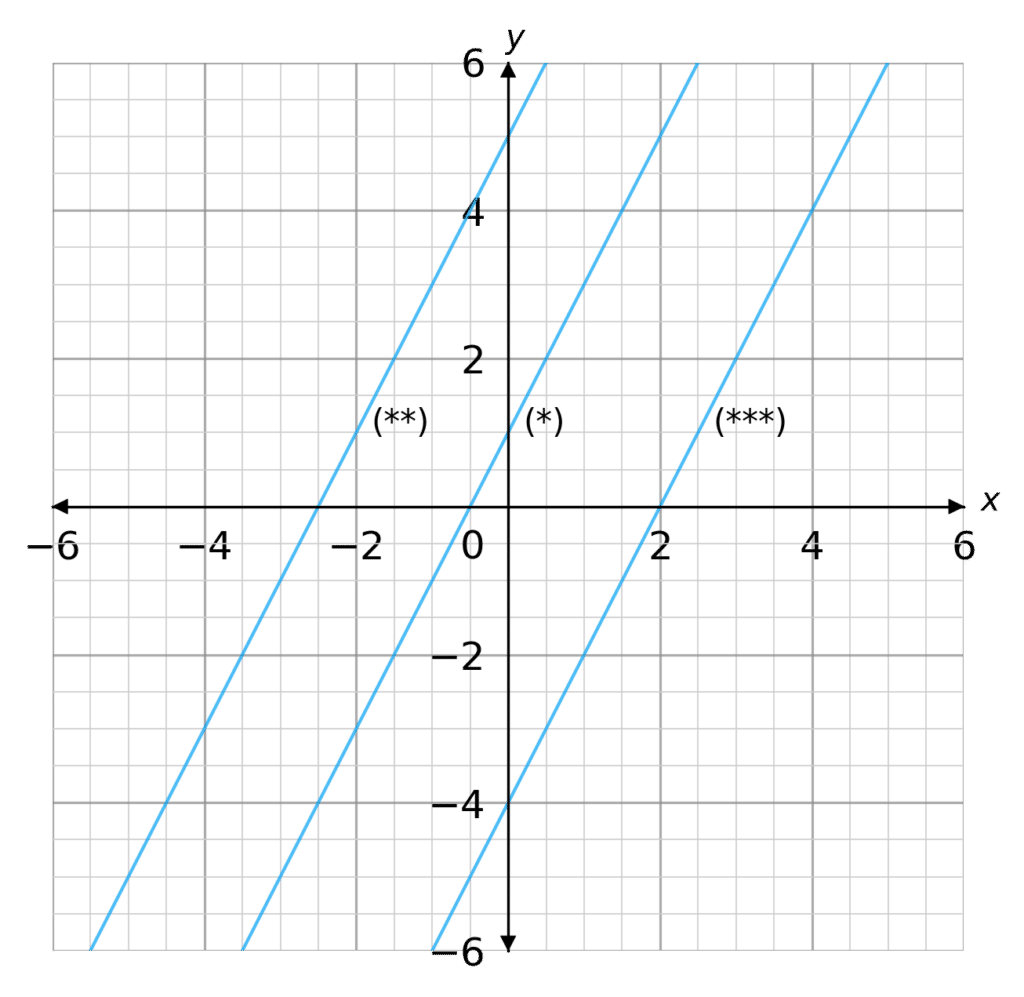
Let’s take a look at the following lines:

$y=\textcolor{#10a6f3}{2}x+1$ (*)

$y\textcolor{#10a6f3}{-2}x=5$ (**)

$y=\textcolor{#10a6f3}{2}x -4$ (***)

The second equation (**) must be rearranged into the form

$y=\textcolor{#10a6f3}{m}x+c$ , before comparing the gradients:

$y=\textcolor{#10a6f3}{2}x+5$

These lines all have a gradient of $\textcolor{#10a6f3}{2} \, (m=2)$ . These straight line equations are shown on the graph to the right.

Perpendicular Lines – Right Angles

Perpendicular lines meet at a right angle. When we multiply the gradients of a pair of perpendicular lines they multiply to $\textcolor{#00d865}{-1}$ .

Another way of looking at this concept is to think of the perpendicular gradient as the ‘opposite sign and reciprocal’.

For instance, let’s say we have a straight line with a gradient: $\textcolor{#00d865}{m=2}$

Then the perpendicular gradient would be: $\textcolor{#00d865}{m=-\dfrac{1}{2}}$

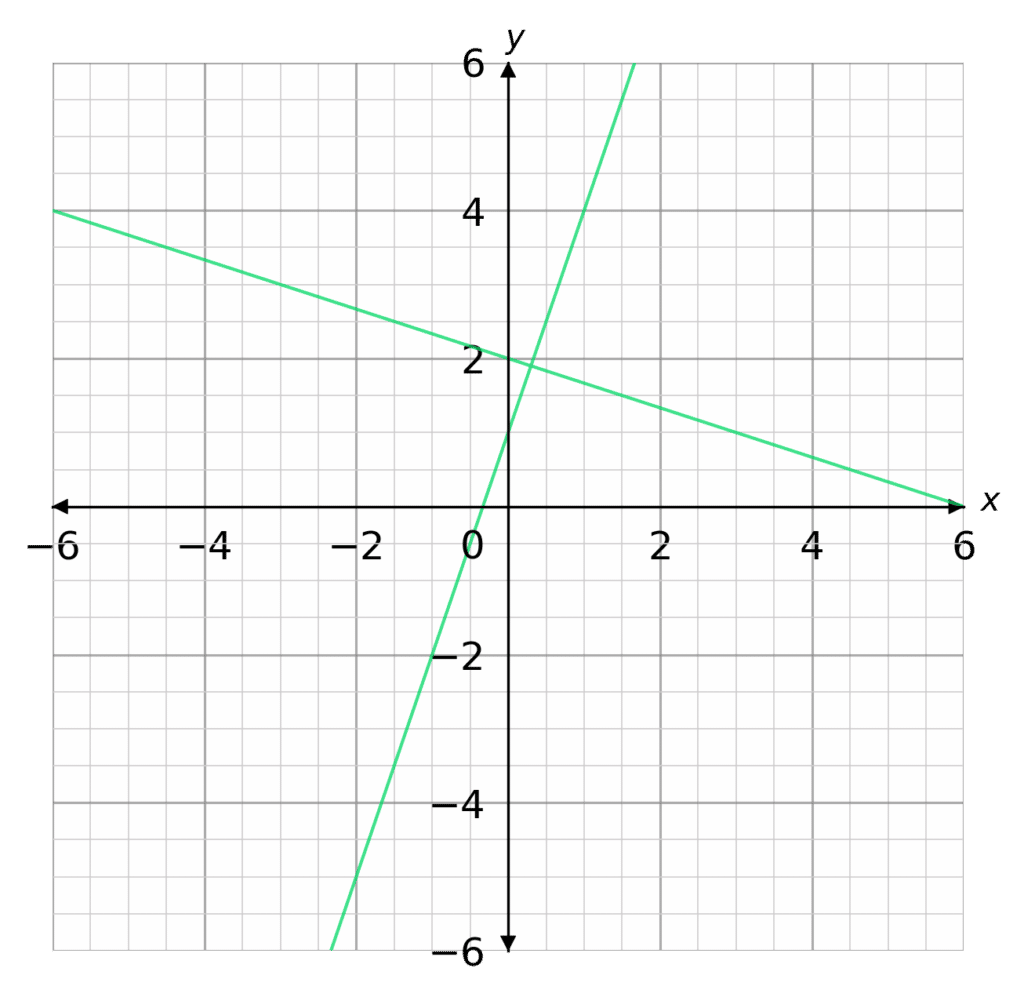
\textcolor{#00d865}{2}\times\textcolor{#00d865}{-\dfrac{1}{2}}=\textcolor{#00d865}{-1}

Let’s take a look at the following lines:

$y=\textcolor{#00d865}{3}x+1$

$y=\textcolor{#00d865}{-\dfrac{1}{3}}x+2$

These lines are perpendicular as: $\textcolor{#00d865}{3}\times\textcolor{#00d865}{-\dfrac{1}{3}}=\textcolor{#00d865}{-1}$ . These straight line equations are shown on the graph to the right.

Example 1: Parallel Lines

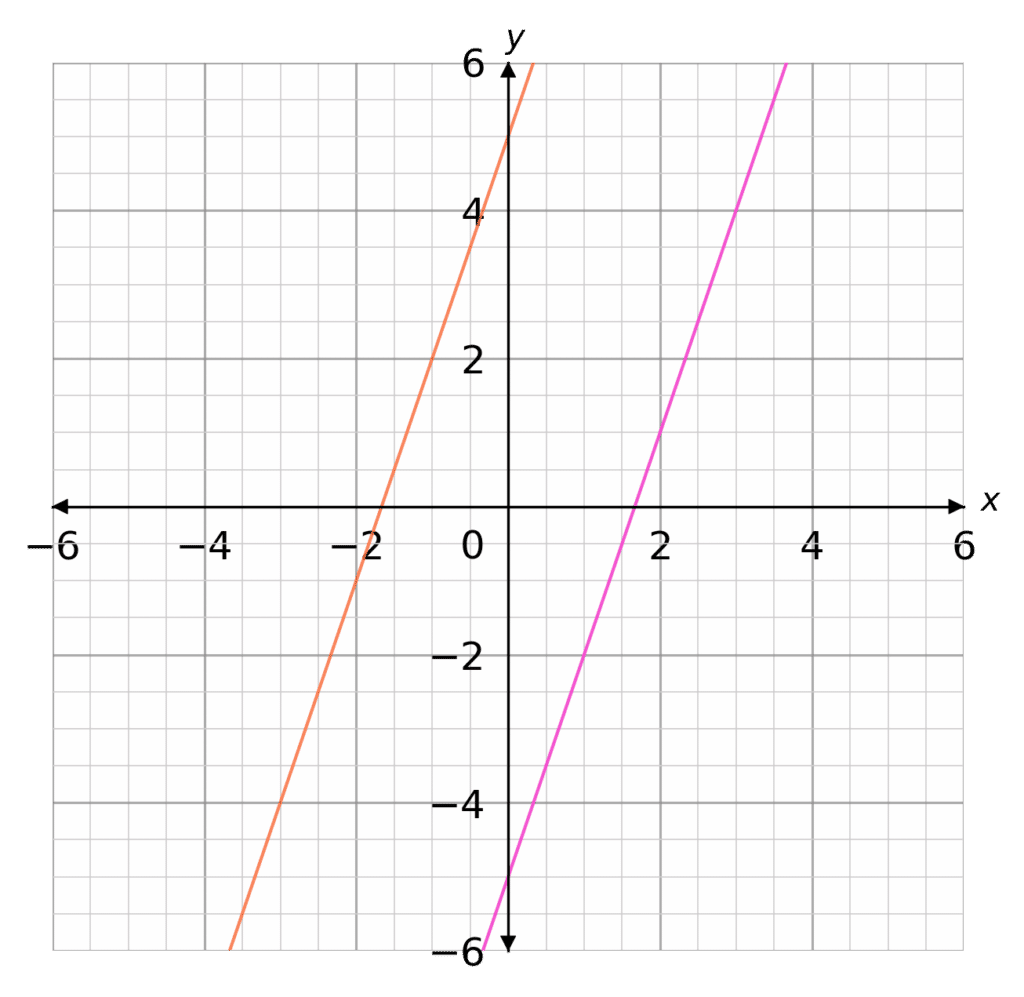
Find the equation of a straight line that is parallel to $\textcolor{#f95d27}{y=3x+5}$ and passes through $(1,-2)$

Equation of the parallel line: $y=3x+c$

[3 marks]

$c$ is the $y \,$ intercept and can take any value. However, because we know the line passes through the coordinate $(1,-2)$ , we can find the exact value of $c$

To do this, we substitute $x=1$ and $y=-2$

-2=3(1)+c \rightarrow c=-5 \rightarrow \textcolor{#f21cc2}{y=3x-5}

Example 2: Perpendicular Lines

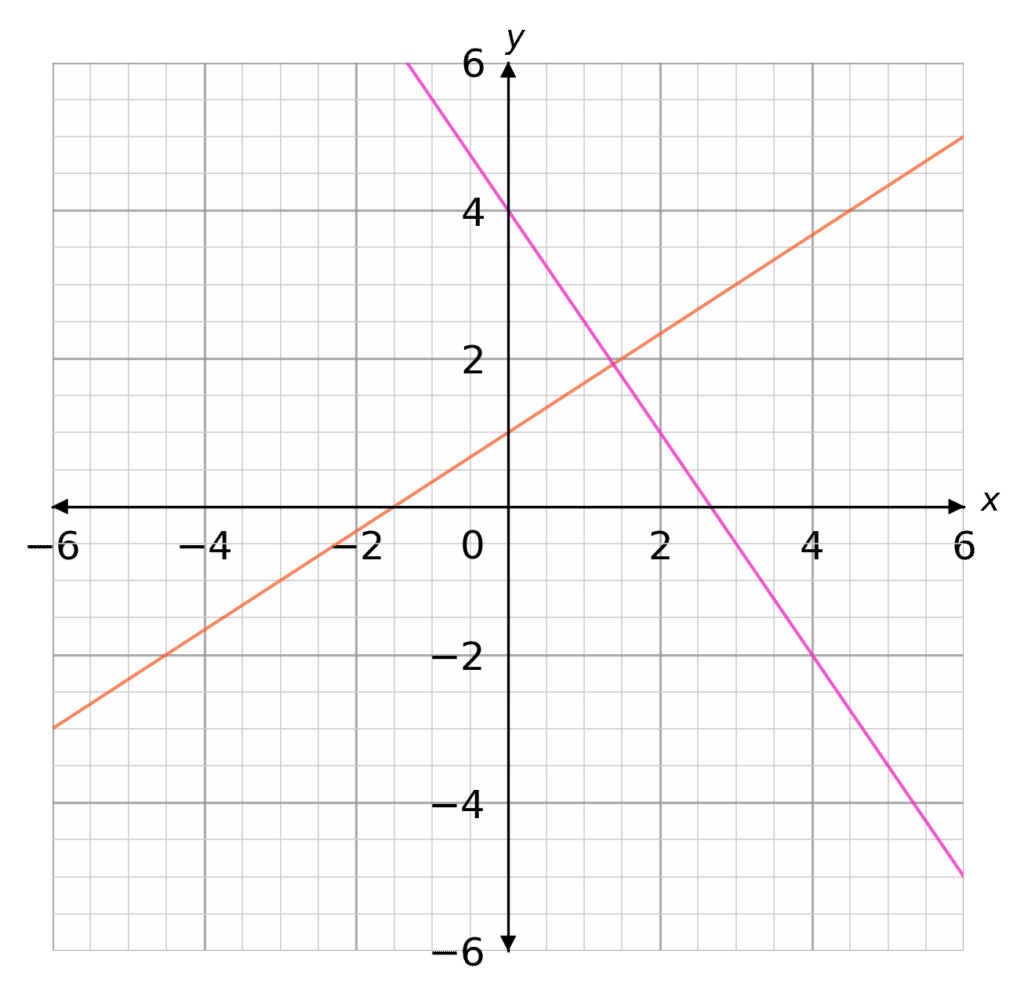
Find the equation of a straight line that is perpendicular to

$\textcolor{#f95d27}{y=\dfrac{2}{3}x+1}$ and passes through $(2,1)$

[3 marks]

Equation of the perpendicular line: $y=-\dfrac{3}{2}x+c$

$c$ is the $y \,$ intercept and can take any value. However, because we know the line passes through the coordinate $(2,1)$ , we can find the exact value of $c$

To do this, we substitute $x=2$ and $y=1$