Revise
Collecting Like Terms
Collecting Like Terms Revision
Collecting Like Terms
A term is an individual part of an expression and typically appears in one of three forms:
- A number by itself
- A letter by itself
- A combination of letters and numbers
Like terms have the same combination of letters. To add or subtract terms with the same letter, we add or subtract the numbers like usual and just put the letter back on the end.
Skill 1: Linear Expressions with a Single Variable
Linear expressions are those in which all variables (i.e. the letters) are to the power of 1 so there are no squared or cubed terms.
Example: simplify the following,
2a + 3 + a + 5
We have to group the terms that are similar; all the terms that are just numbers need grouping together and simplifying, as do the similar algebraic terms.
This gives,
2a+1a = 3a
3 + 5 = 8
This gives the final answer to be,
2a + 3 + a + 5 = 3a + 8
Note: Normally the 1 in front of the a is left out but we have included it here to make it clear the steps being taken.
Skill 2: Like Terms With Different Letters
Sometimes terms have more than one variable (letter) multiplied or divided together:
\textcolor{red}{xy} + \textcolor{blue}{y} + \textcolor{red}{2xy}
in this instance, \textcolor{red}{xy} and \textcolor{red}{2xy}, are like terms that can be added together to simplify the expression, hence we find,
\textcolor{red}{3xy} + \textcolor{blue}{y}
Skill 3: Identifying Like Terms with Powers
Terms of certain powers have to be grouped with terms of the same power. Such terms can also include multiple letters and powers.
2\textcolor{red}{x^2y} + \textcolor{blue}{xy^2} + 3\textcolor{red}{x^2y} + 5\textcolor{blue}{xy^2} = 5\textcolor{red}{x^2y} + 6\textcolor{blue}{xy^2}
- 2\textcolor{red}{x^2y} and 3\textcolor{red}{x^2y} are like terms
- \textcolor{blue}{xy^2} and 5\textcolor{blue}{xy^2} are like terms
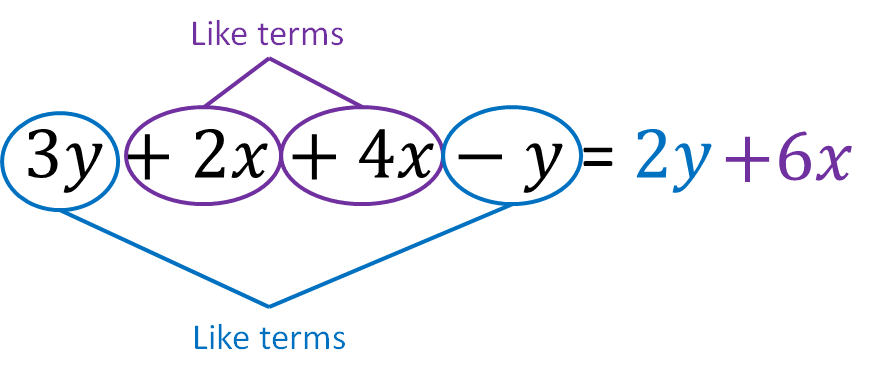
Example 1: Two Variables
Simplify the expression 3y+2x+4x-y.
[1 mark]
\textcolor{blue}{3y} and -\textcolor{blue}{y} are like terms
\textcolor{purple}{2x} and \textcolor{purple}{4x} are like terms
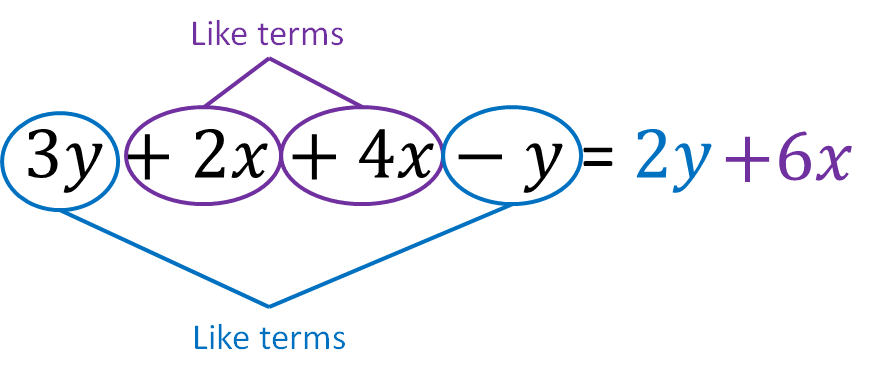
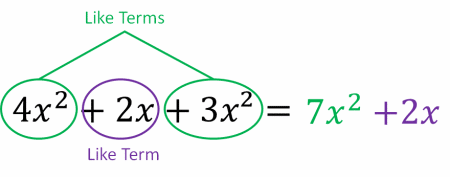
Example 2: Including Powers
Simplify the expression 4x^2 +2x +3x^2.
[1 mark]
\textcolor{limegreen}{4x^2} and \textcolor{limegreen}{3x^2} are like terms
\textcolor{purple}{2x} has no like terms
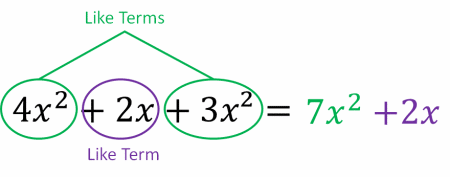
Example 3: Multiple Letters
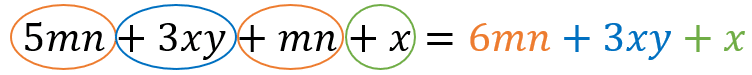
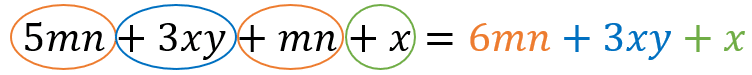
Simplify the expression 5mn +3xy+mn+x.
[1 mark]
\textcolor{maroon}{5mn} and \textcolor{maroon}{mn} are like terms
\textcolor{blue}{3xy} and \textcolor{limegreen}{x} have no other like terms
Example 4: Multiple Letters and Powers
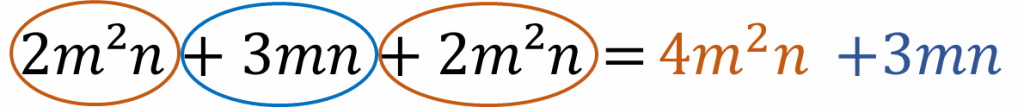
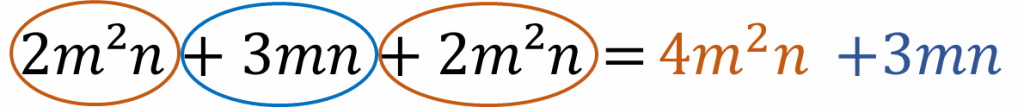
Simplify the expression 2m^2n+3mn+2m^2n.
[1 mark]
\textcolor{maroon}{2m^2n} and \textcolor{maroon}{2m^2n} are like terms
\textcolor{blue}{3mn} has no like terms
Collecting Like Terms Example Questions
Question 1: Simplify the following expression by collecting like terms:
[1 mark]
5x+5-2x+3-4-x
It is often easier to first group the similar terms together, before simplifying,
5x+5-2x+3-4-x \\ =(5x-2x-x)+(5+3-4) \\ =2x+4
Question 2: Simplify the following expression by collecting like terms:
[1 mark]
ab+bc+2ab-bc+a
It is often easier to first group the similar terms together, before simplifying,
ab+bc+2ab-bc+a \\ = a+(ab+2ab)+(bc-bc) \\ = a+3ab
Question 3: Simplify the following expression by collecting like terms:
[1 mark]
11x+7y-2x-13y
It is often easier to first group the similar terms together, before simplifying:
11x+7y-2x-13y \\ = (11x-2x)+(7y-13y) \\ =9x-6y
Question 4: Simplify the following expression by collecting like terms:
[1 mark]
2m+6n-3+8n +5m
It is often easier to first group the similar terms together, before simplifying:
2m+6n-3+8n+5n \\ = (2m+5m)+(6n+8n)-3 \\ = 7m+14n-3
Question 5: Simplify the following expression by collecting like terms:
[1 mark]
2a^2 + 5b-2a -3b+5a^2
It is often easier to first group the similar terms together, before simplifying:
2a^2 + 5b-2a -3b+5a^2\\ = (2a^2+5a^2)+(5b-3b)-2a \\ =7a^2+2b-2a
Collecting Like Terms Worksheet and Example Questions
(NEW) Collecting like terms Exam Style Questions - MME
Level 1-3GCSENewOfficial MME
