Revise
Circle Theorems
Circle Theorems Revision
The 8 Circle Theorems
You should be familiar with all 8 circle theorems to the point where:
a) You can identify when they should be used.
b) You can describe which one you’ve used with appropriate language.
Make sure you are happy with the following topics before continuing
Note: Circle geometry problems often require knowledge of all the basic geometry rules in order to solve them.
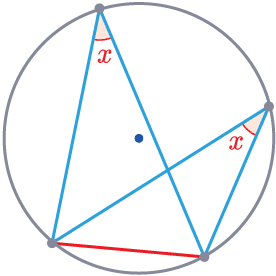
Rule 1
Angles in the same segment are equal.
\textcolor{red}{x} = \textcolor{red}{x}
Triangles drawn from the same chord will have the same angle when touching the circumference.
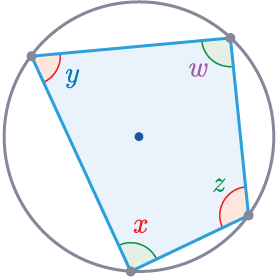
Rule 2
Opposite angles in a cyclic quadrilateral add up to 180\degree.
\textcolor{purple}{w}+\textcolor{red}{x}=180\degree
\textcolor{blue}{y}+\textcolor{limegreen}{z}=180\degree
This is a 4 sided shape with every corner touching the circumference of the circle.
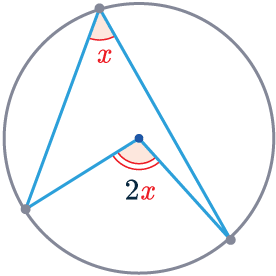
Rule 3
The angle at the centre is twice the angle at the circumference.
The angle formed at the centre is exactly twice the angle at the circumference of a circle.
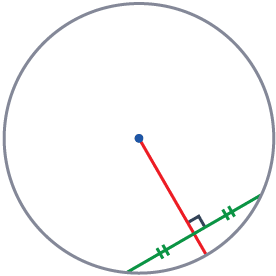
Rule 4
The perpendicular bisector of a chord passes through the centre of the circle.
A line perpendicular and in the centre of a chord (a line drawn across the circle) will always pass through the centre of the circle.
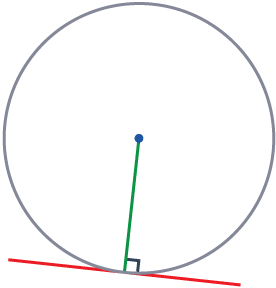
Rule 5
The radius will always meet a tangent to the circle at 90\degree.
A tangent (a line touching a single point on the circumference) will always make an angle of exactly 90\degree with the radius.
You can say that a tangent and radius that meet are perpendicular to each other.
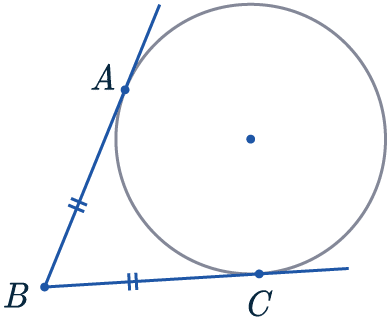
Rule 6
The tangents from the same point to a circle are equal in length.
AB = BC
Two tangents (a line touching a single point on the circumference) drawn from the same outside point are always equal in length.
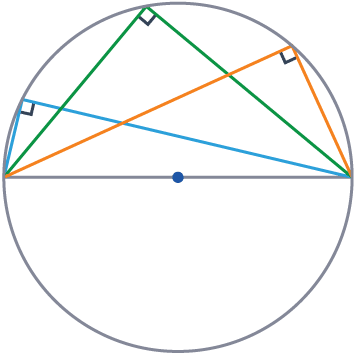
Rule 7
The angle inscribed in a semicircle is always a right angle.
A triangle drawn with the diameter will always make a 90\degree angle where it hits the circumference.
Another way of saying this is that a diameter ‘subtends’ a right-angle at the circumference.
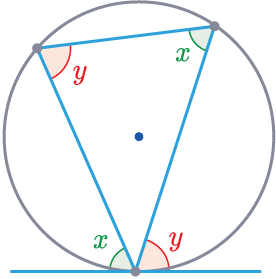
Rule 8
Alternate Segment Theorem: The angle between the tangent and the side of the triangle is equal to the opposite interior angle.
\textcolor{limegreen}{x}=\textcolor{limegreen}{x}
\textcolor{red}{y}=\textcolor{red}{y}
The angle between the tangent and the triangle will be equal to the angle in the alternate segment.
(This is the hardest rule and can be tricky to spot).
Proving Circle Theorems
You may be asked to give proof of some of these circle theorems. This is a difficult exercise in mathematical thinking.
Usually constructing triangles can help with the proofs, as then we can use properties of triangles to make deductions.
Example:
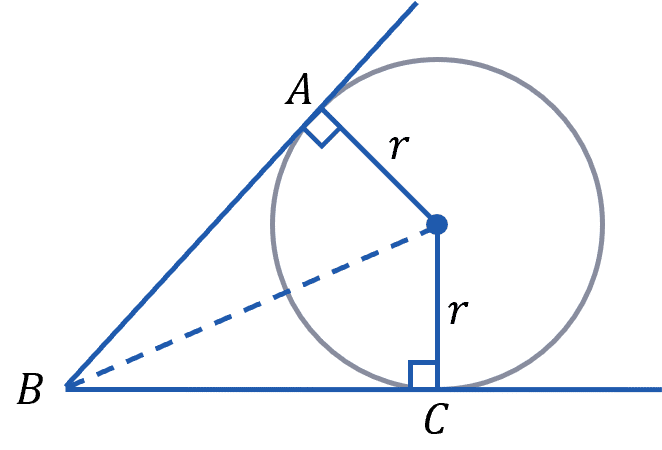
Here we can prove rule 6 by constructing triangles. Where the two tangents meet the circle, we can create a base of a right angle triangle with the radius of the circle, r, then the hypotenuse is the line from the centre of the circle to the point where the tangents meet.
We know these are congruent triangles as they are right angled and have the same hypotenuse and base, so the third side must also be the height must also be the same.
This height is the length of the tangent from the circumference to their intersect.
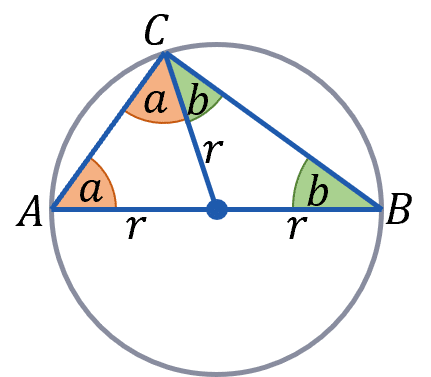
Another example would be rule 7, if a triangle is inscribed in a semicircle, it can be inscribed in a circle along the diameter.
Then we may split the triangle into two triangles, from the centre of the circle to the peak of the triangle. In this case AB is the diameter so the peak is point C. As this new line is from the centre to the circumference the circumference, its length is the radius, r.
This gives us two isosceles triangles, both with two sides of length r. If we say the triangle with points A, C and the centre has base angles a, and the other triangle, with points B, C and the centre has base angles b, then the original triangle, inscribed in the semicircle has angles, a, a+b and b. As the angles in a triangle add up to 180\degree
2a+2b= 180\degree
a+b = 90 \degree
As \angle ACB = a+b = 90 \degree
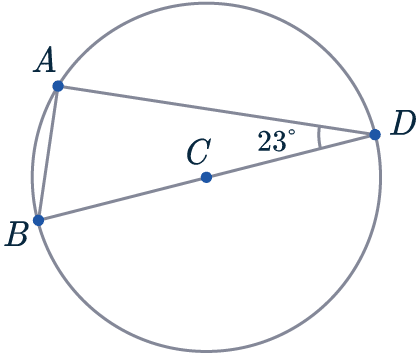
Example 1: Angle in a Semi-Circle
Below is a circle with centre C.
BD is a diameter of the circle, A is a point on the circumference.
What is the size of angle CBA?
[2 marks]
If a question says “show our workings”, you must state what circle theorem/geometry fact you use when you use it.
BD is a diameter of the circle, we know that triangle BAD is confined within the semi-circle.
So we can use Rule 7, the angle in a semi-circle is a right-angle to deduce that \angle BAD = 90\degree.
To find CBA, we just need to subtract from 180\degree.
\angle CBA = 180\degree - 23\degree - 90\degree = 67\degree
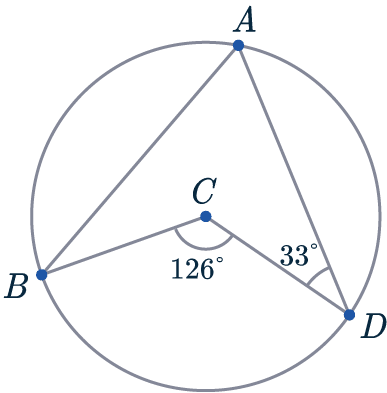
Example 2: Combining Rules
Below is a circle with centre C.
A, B, and D are points on the circumference.
Angle \angle BCD is 126\degree and angle \angle CDA is 33\degree.
Find angle ABC.
You must show your workings.
[2 marks]
The first circle theorem we’re going to use here is: Rule 3, the angle at the centre is twice the angle at the circumference.
The angle at the centre is 126\degree, so;
\angle BAD = 126\degree \div 2 = 63\degree.
We now know two out of the four angles inside ABCD.
To find a third, simply observe that angles around a point sum to \textcolor{orange}{360\degree}:
360\degree - 126\degree = 234\degree
Since the angles in a quadrilateral sum to \textcolor{orange}{360\degree}, we can find the angle we’re looking for.
\angle ABC= 360\degree - 33\degree - 63\degree - 234\degree = 30 \degree
Example 3: Proof of Circle Theorems
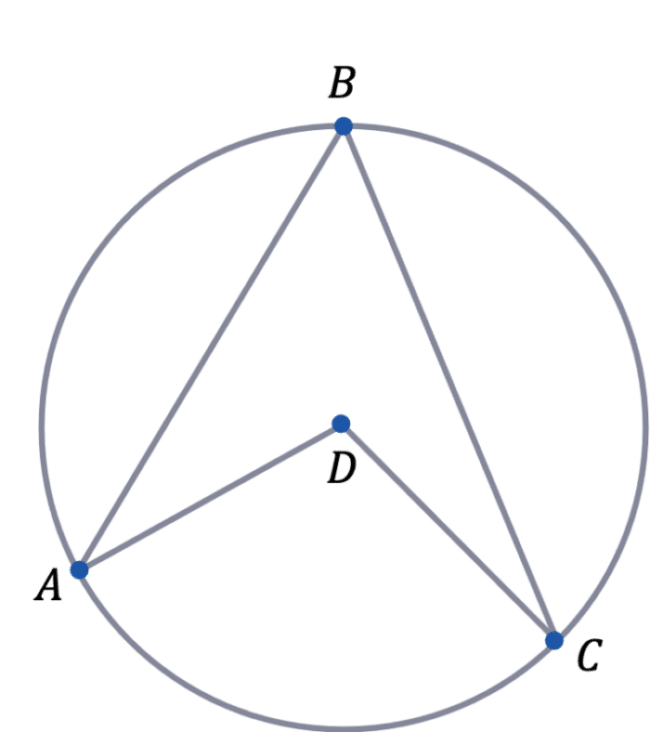
The circle to the right has centre D
A, B and C are points on the circumference of the circle.
Prove that \angle ADC = 2\angle ABC
[4 marks]
Here we are trying to prove rule 3. By drawing a line from the centre D to the point B, we create two isosceles triangles. This is because AD, BD and CD are all radii.
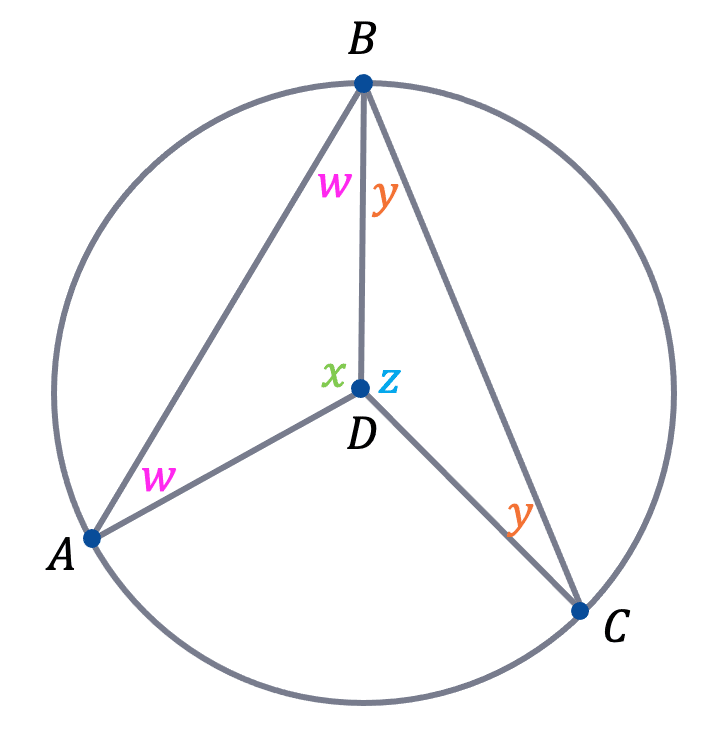
As triangle ADB and BDC are isosceles, they must have two equal angles – the two not at the centre. This is shown in the diagram to the right.
The sum of angles inside any triangle is 180\degree, therefore:
2\textcolor{#FF00FF}{w}+\textcolor{#00d865}{x}=180 \rightarrow \textcolor{#00d865}{x}=180-2\textcolor{#FF00FF}{w}
2\textcolor{#f95d27}{y}+\textcolor{#10a6f3}{z}=180 \rightarrow \textcolor{#10a6f3}{z}=180-2\textcolor{#f95d27}{y}
Let angle \angle ADC = a and \angle ABC = b
Angles around a point add up to 360\degree, therefore:
a+\textcolor{#00d865}{x}+\textcolor{#10a6f3}{z}=360
a+(180-2\textcolor{#FF00FF}{w})+(180-2\textcolor{#f95d27}{y})=360
a+360-2\textcolor{#FF00FF}{w}-2\textcolor{#f95d27}{y}=360
a=2(\textcolor{#FF00FF}{w}+\textcolor{#f95d27}{y})
Using the fact that \textcolor{#FF00FF}{w}+\textcolor{#f95d27}{y}=b, we have shown that a=2b and hence proving the circle theorem.
Circle Theorems Example Questions
Question 1: Points A, B, and C all lie on the circumference of a circle with centre O.
Work out the value of angle x. Give a reason for each step of your answer.
[2 marks]
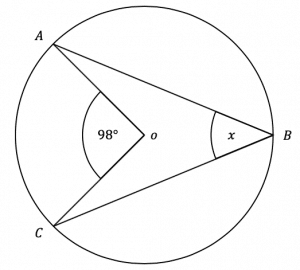
The angle at the centre is twice the angle at the circumference. Given that the angle formed at the centre, which in this case is 98\degree, is exactly twice the angle at the circumference of a circle at the same point. We simply have to divide the angle at the centre of the circle by two:
x=98\degree \div 2 = 49\degree
Question 2: Points A, B, and C all lie on the circumference of a circle and the line BC passes through the centre of the circle, O.
Work out the value of angle x. Give a reason for each step of your answer.
[2 marks]
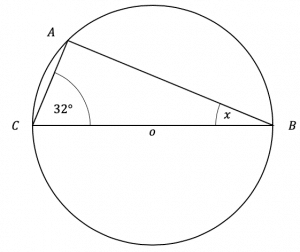
The angle in a semicircle is always a right angle. Given that any triangle drawn with the diameter will always make a 90° angle where it hits the opposite circumference. We can also use that interior angles in a triangle add up to 180°, we find that,
x=180\degree - 90\degree - 32\degree = 58\degree
Question 3: Below is a circle with centre C. A, B, D, and E are points on the circumference. BD is a diameter of the circle.
Angle CDA is 18\degree and angle DAE is 31 \degree. Find the size of angle EDA. You must show your workings.
[3 marks]
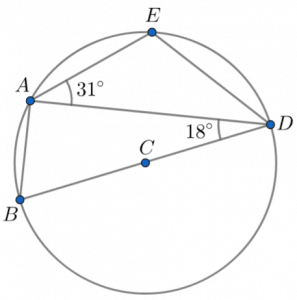
Firstly, recognise that since BD is a diameter, angle BAD is the angle in a semi-circle. Our circle theorems tell us that the angle in a semi-circle is a right-angle so BAD must be 90\degree. As we now know this, we get that
\text{Angle BAE } = 90 + 31 = 121 \degree.
Next, we recognise that ABDE is a cyclic quadrilateral. On a related note, the second circle theorem we’re going to use is: opposite angles in a cyclic quadrilateral sum to 180. Angle BAE (which we just worked out) is opposite to angle CDE, so
\text{Angle CDE } = 180 - 121 = 59\degree
Then, the final step to finding angle EDA will be subtracting the size of angle CDA from that of angle CDE to get
\text{Angle EDA } = 59 - 18 = 41\degree.
Question 4: Below is a circle with centre C. A, E, and D are points on the circumference. AB and BD are tangents to the circle.
Angle ABD is 42\degree. Find the size of angle AED. You must show your workings.
[3 marks]
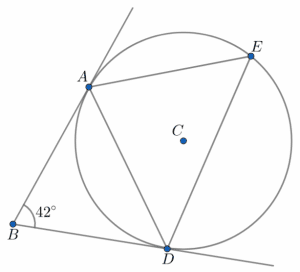
Our first circle theorem here will be: tangents to a circle from the same point are equal, which in this case tells us that AB and BD are equal in length.
This means that ABD must be an isosceles triangle, and so the two angles at the base must be equal. In this case those two angles are angles BAD and ADB, neither of which know. Let the size of one of these angles be x, then using the fact that angles in a triangle add to 180, we get
x + x + 42 = 180\degree.
Then, subtract 42 from both sides to get
2x = 180 - 42 = 138\degree,
and divide both sides by 2 to get
x = 69\degree.
Now we can use our second circle theorem, this time the alternate segment theorem. This tells us that the angle between the tangent and the side of the triangle is equal to the opposite interior angle. Given that angle ADB, which is 69\degree, is the angle between the side of the triangle and the tangent, then the alternate segment theorem immediately gives us that the opposite interior angle, angle AED (the one we’re looking for), is also 69\degree.
Question 5: Below is a circle with centre O. A, B, and C are points on the circumference. A tangent to the circles passes through point A.
Given that angle BAC is 23\degree and angle ACB is 71\degree, find the size of angle x\degree.
You must show your workings.
[3 marks]
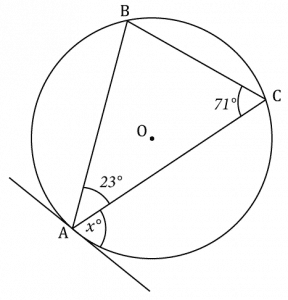
Firstly, using the fact angles inside of a triangle add together to 180\degree. Angle ABC is,
180\degree-71\degree-23\degree=86\degree
The Alternate Segment Theorem states the angle between the tangent and the side of the triangle is equal to the opposite interior angle, hence
x\degree=\angle \text{ABC} = 86 \degree.
Question 6: Below is a circle with centre E. A, B, Cand D are points on the circumference.
\angle ABD =x and \angle ACD = y.
Prove that x = y
[3 marks]
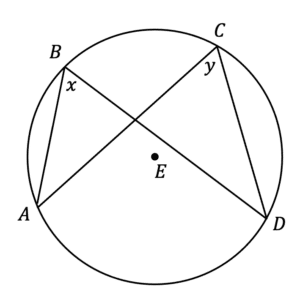
Firstly, by adding a chord connecting A and D. We now have two segments. Next we draw two lines connecting from A and D to the centre, forming a third isosceles triangle.
\angle AED =z
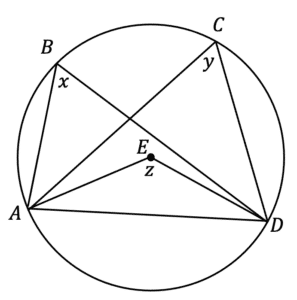Based on the circle theorem: ‘the angle at the centre is twice the angle at the circumference’, we know that x must be half the size of z, similarly for y.
Therefore x=y
Circle Theorems Worksheet and Example Questions
(NEW) Circle Theorems Exam Style Questions - MME
Level 6-7GCSENewOfficial MMECircle Theorems Drill Questions
Circle Theorems
Level 8-9GCSE
