Revise
Bearings
Bearings Revision
Bearings
Bearings are a way of expressing the angle between two objects. There is a specific set of rules about how bearings should be calculated and expressed.
1. Always measure bearings from the North line.
2. Always express your answers as three-figure bearings (so 60\degree would be 060\degree).
3. Always draw and measure bearings clockwise.
Understanding angles on parallel lines is required for this topic.
Skill 1: Bearings – 3 Rules
There is a specific set of rules about how bearings should be calculated and expressed.
1. Always measure bearings from the North line.
2. Always express your answers as three-figure bearings (so 60\degree would be 060\degree).
3. Always draw and measure bearings clockwise.
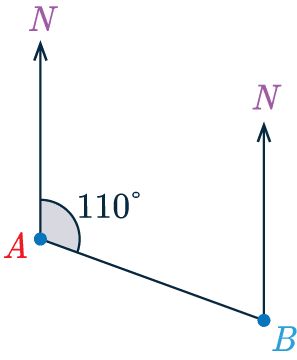
Example 1: Measure a Bearing
Find the bearing of \textcolor{blue}{B} from \textcolor{red}{A}.
[1 mark]
Note: the terminology “B from A” is always used, as opposed to “A to B”.
So, we have our two points and a North line coming off both.
The bearing of \textcolor{blue}{B} from \textcolor{red}{A} is measured from the North line going clockwise until we hit the straight line.
Then using a protractor, we measure the angle to be 110\degree which is the bearing of \textcolor{blue}{B} from \textcolor{red}{A}.
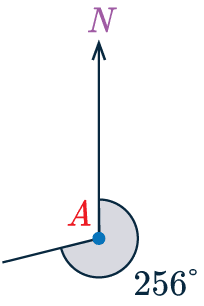
Example 2: Drawing Bearings
Two boats \textcolor{red}{A} and \textcolor{blue}{B} are 5km apart, and the bearing of \textcolor{blue}{B} from \textcolor{red}{A} is 256\degree.
Using the scale 1\text{ cm}:1\text{ km}, construct a diagram showing the relative positions of points \textcolor{red}{A} and \textcolor{blue}{B}.
[2 marks]
First, we draw point \textcolor{red}{A} with a North line and measure an angle of 104\degree going anticlockwise from it (This is because 360 - 254 = 104\degree. You can’t measure 256\degree using a protractor any other way).
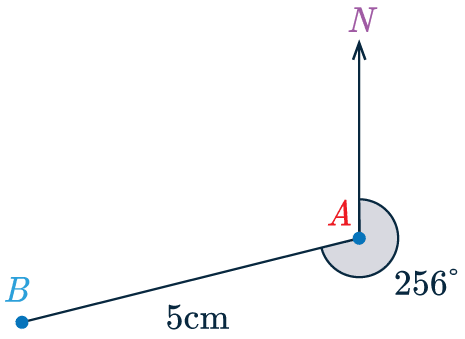
Then, as \textcolor{red}{A} and \textcolor{blue}{B} are 5 km apart, we will need to make the line from \textcolor{red}{A} to \textcolor{blue}{B} (going along the bearing we’ve determined) 5 cm long.
The result of this is below, not drawn accurately.
Example 3: Finding Bearings
The diagram below shows the bearing of \textcolor{blue}{B} from \textcolor{red}{A}.
Find the bearing of \textcolor{red}{A} from \textcolor{blue}{B}.
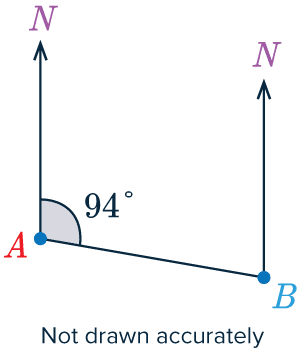
[2 marks]
Now, we can’t measure the angle because the diagram is not drawn accurately.
We will use the fact that both North lines are parallel and extend the line \textcolor{red}{A}\textcolor{blue}{B} past point \textcolor{blue}{B}, the angle formed by the North line at \textcolor{blue}{B} and the extension to line \textcolor{red}{A}\textcolor{blue}{B} and the bearing of \textcolor{blue}{B} from \textcolor{red}{A} are corresponding angles (also known as an “F angle”).
So, from our knowledge of parallel lines, we know that they must be equal.
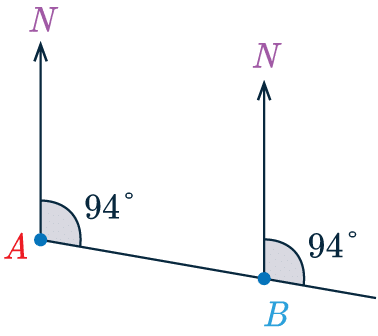
Finally, we are measuring the line of \textcolor{red}{A} from \textcolor{blue}{B} so we need to go clockwise from the north line at \textcolor{blue}{B} to the line \textcolor{red}{A}\textcolor{blue}{B}.
We have 94\degree but need the remaining portion of the angle.
Fortunately, the remaining portion of the angle is just a straight line, so the bearing of \textcolor{red}{A} from \textcolor{blue}{B} is
94 + 180 = 274\degree
Bearings Example Questions
Question 1: A boat and a lighthouse are 70 miles apart. The bearing of the lighthouse from the boat is 051\degree.
Using the scale 1 cm : 10 miles, construct a diagram showing the relative positions of the lighthouse and the boat.
[2 marks]
Let the lighthouse be L and the boat be B. As we’re finding the bearing of L from B, we shall measure an angle of 051\degree clockwise at B.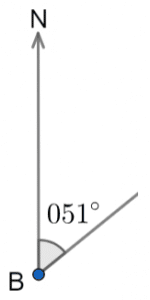 
Then, as B and L are 70 miles apart, we will need to make the line from B to L 7cm long. The final diagram should look like,
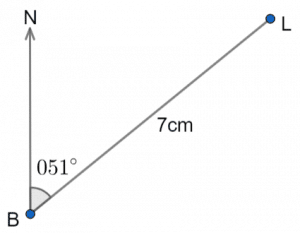
Question 2: The diagram below shows the bearing of A from B. Find the bearing of B from A.
[2 marks]
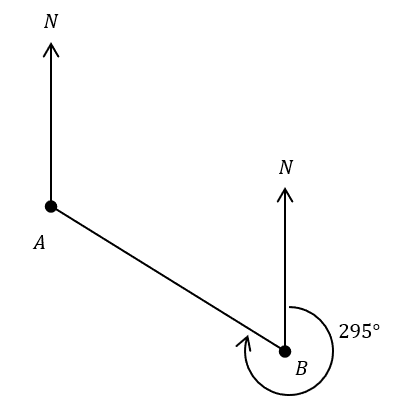
We can find the other angle around the point B by subtracting 295 from 360,
360\degree - 295\degree = 65 \degree
Then, because the two North lines are parallel, we can say that the bearing of B from A and the 65\degree angle we just found are co-interior. These two angles (marked with red below) must add to 180.
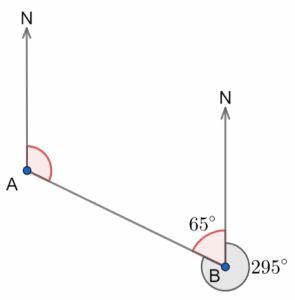
So, we get:
\text{Bearing of B from A } = 180\degree - 65\degree = 115\degree
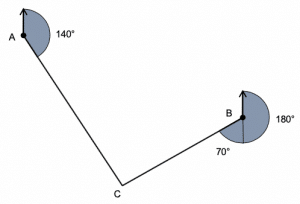
Question 3: The location C is on a bearing of 140 \degree from A. The bearing of C from B is 250 \degree. Find the location C and mark it on the diagram below.
[2 marks]
Drawing straight lines along each of the bearings, we can find C at the point of intersection of both lines.
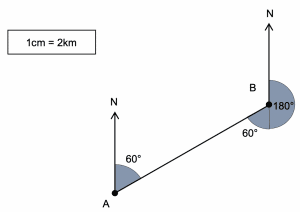
Question 4: By measuring the diagram given, state the bearing of B from A.
[1 mark]
By use of a protractor or otherwise we find the angle of 60 degrees. This written as a bearing is,
060 \degree
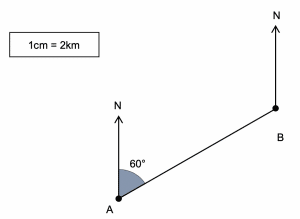
Question 5: A diagram of a bearing is shown below. Given that the bearing of B from A is 060 \degree, state the bearing of A from B.
[3 marks]
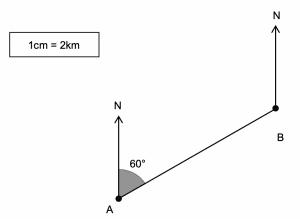
The two North lines are parallel, so we can say that the bearing of B from A and the co-interior angle at B must add to 180 degrees. Thus the co-interior angle is
180 \degree-60\degree = 120 \degree
As angles around a point sum to 360 degrees we can find the bearing of A from B as,
360 \degree-120 \degree=240 \degree
Bearings Worksheet and Example Questions
(NEW) Bearings Exam Style Questions - MME
Level 4-5GCSENewOfficial MMEBearings Drill Questions
Bearings - Drill Questions
Level 4-5GCSE
