Revise
Pythagoras
Pythagoras Revision
Pythagoras
Pythagoras’ theorem is an equation that describes a relationship between the 3 sides of a right-angled triangle. We can use it to determine a missing length when given the two other lengths.
Make sure you are happy with the following topics before continuing.
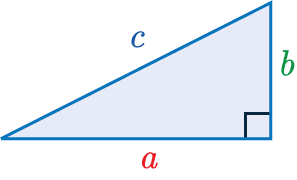
Pythagoras’ Theorem
The equation is:
\textcolor{red}{a}^2+\textcolor{limegreen}{b}^2=\textcolor{blue}{c}^2
where \textcolor{blue}{c} is the hypotenuse and \textcolor{red}{a} and \textcolor{limegreen}{b} are the two other sides. The hypotenuse is always the longest side of the triangle and can be found opposite the right angle.
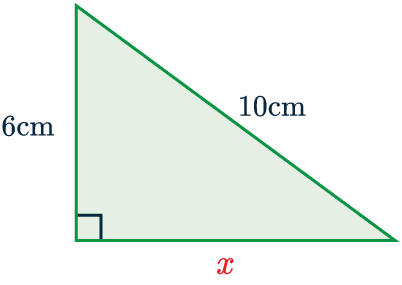
Example 1: Finding a Length
Find the length of the side marked \textcolor{red}{x} on the right angled triangle shown.
[2 marks]
In order to find this using Pythagoras’ theorem, we need to work out which side corresponds to each of the letters \textcolor{red}{a}, \textcolor{limegreen}{b}, and \textcolor{blue}{c} in the equation.
\textcolor{blue}{c} = \textcolor{blue}{10} cm
\textcolor{limegreen}{b} = \textcolor{limegreen}{6} cm
\textcolor{red}{a} = \textcolor{red}{x}
Then we can substitute our values in so the equation a^2+b^2=c^2 becomes:
\textcolor{red}{x}^2+\textcolor{limegreen}{6}^2=\textcolor{blue}{10}^2
\textcolor{red}{x}^2+\textcolor{limegreen}{36}=\textcolor{blue}{100}
Now we can solve for \textcolor{red}{x}
\textcolor{red}{x}^2=\textcolor{blue}{100}-\textcolor{limegreen}{36}=64.
\textcolor{red}{x}=\sqrt{64}=8 cm.
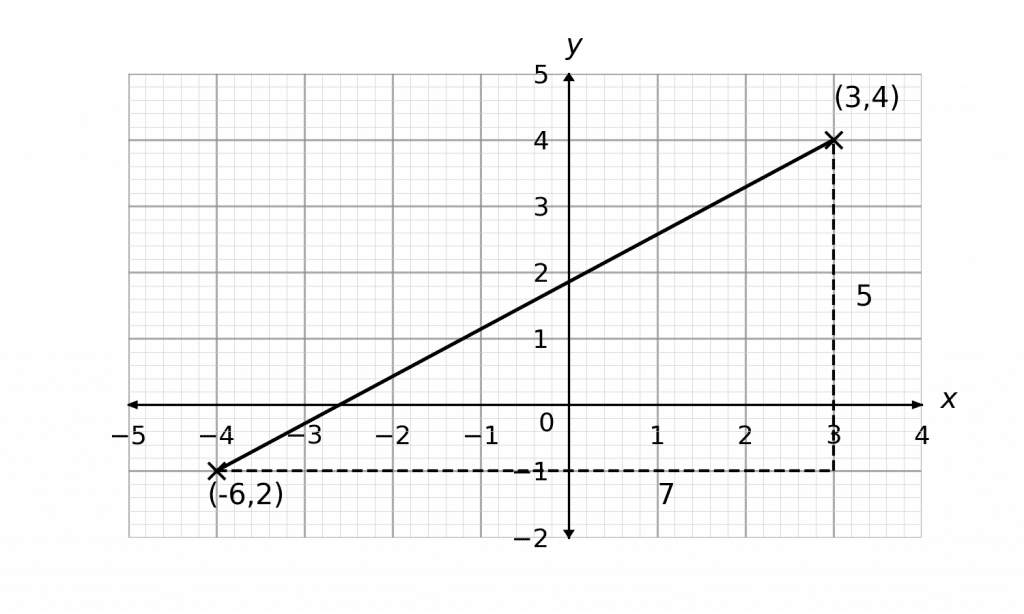
Example 2: Calculating the Length of a Line
Calculate the distance between (-4, -1) and (3, 4).
Give your answer to 1 dp.
[2 marks]
First we plot the two points on a pair of axes, draw a line connecting them and then draw a triangle underneath making a note of the lengths of the sides:
Side 1 (height) = 4 -(-1) = \textcolor{red}{5}
Side 2 (width) = 3 -(-4) = \textcolor{limegreen}{7}
Next we substitute these lengths into Pythagoras’ theorem:
\textcolor{red}{a}^2+\textcolor{limegreen}{b}^2 = \textcolor{blue}{c}^2
\begin{aligned} \textcolor{blue}{c}^2 &= \textcolor{red}{5}^2+\textcolor{limegreen}{7}^2 \\ \textcolor{blue}{c}^2 &= \textcolor{red}{25}+\textcolor{limegreen}{49}=74 \\ \textcolor{blue}{c} &= \sqrt{74}=8.602325267... \\ \textcolor{blue}{c} &= 8.6 \, \, (1 \text{ dp}) \end{aligned}
Note: The length you are trying to calculate, when finding the length of a line between two points, will always be the hypotenuse.
Pythagoras Example Questions
Question 1:
Find length BC.
Give your answer to 1 decimal place.
[2 marks]
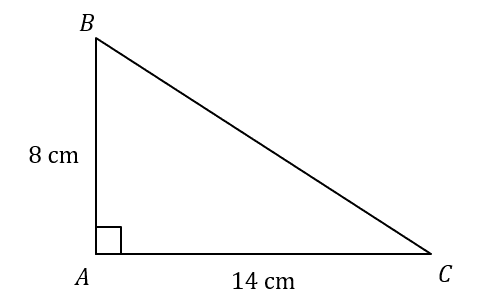
The missing side is the hypotenuse, by substituting the 2 sides we know into the equation a^2+b^2=c^2 we get:
8^2+14^2=c^2
Evaluating the two squares gives us:
c^2=64+196
c^2=260
Then square rooting both sides of the equation gives us:
BC=\sqrt{260}=16.1245155...
= 16.1 cm (1 dp).
Question 2: Work out the distance between the two points (-6, 2) and (4, 5).
Give your answer to 3 significant figures.
[2 marks]
To do this, we plot the points on a graph and draw a line connecting them. We then construct a right-angled triangle. The resulting picture looks like: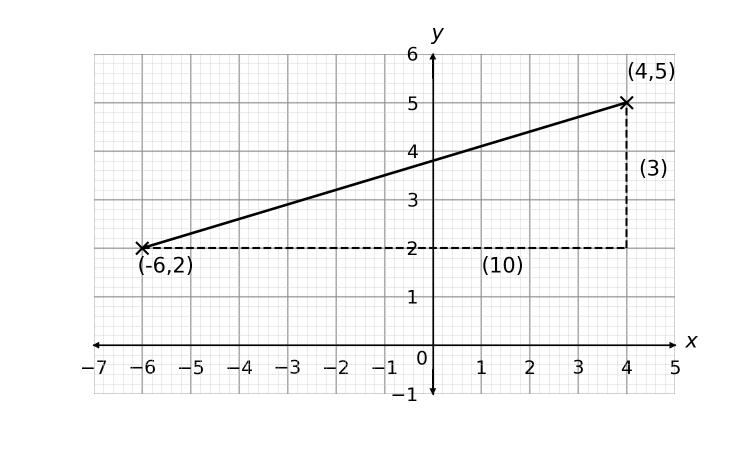
We can see that the distance between the two points is the longest side of a right-angle triangle – the hypotenuse, so by substituting the known sides into the equation a^2+b^2=c^2 we get:
10^2+3^2=c^2
Evaluating the squares gives us:
c^2=100+9
c^2=109
Finally, by square rooting both sides, we get:
c=\sqrt{109}=10.44030651...
= 10.4 cm (3 sf).
Question 3: PQR is a right-angled triangle. Work out the length of the missing side, QR, to 1 decimal place.
[2 marks]
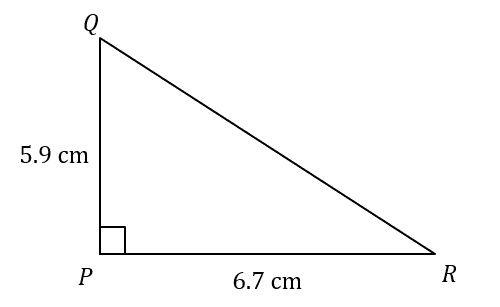
The missing side is the hypotenuse, so by substituting the known sides into the equation a^2+b^2=c^2 we get:
5.9^2+6.7^2=c^2
Evaluating the two squares gives us:
c^2=34.81+44.89
c^2=79.7
Then by square rooting both sides of this equation, we get:
QR=\sqrt{79.7}=8.927485648...
QR=8.9cm (1 dp).
Question 4: LMN is a right-angled triangle. Work out the length of the missing side, LN, to 1 decimal place.
[2 marks]
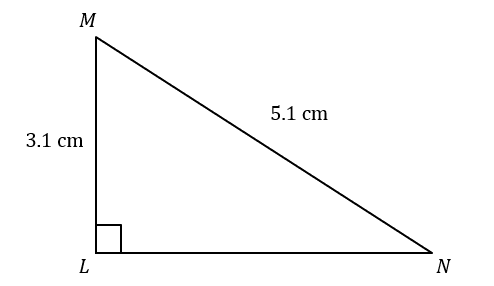
By substituting the known sides into Pythagoras’ Theorem c^2=a^2+b^2 becomes:
5.1^2=LN^2+3.1^2
Next we evaluate the two squares to give us:
26.01=LN^2+9.61
Subtracting 9.61 from both sides:
16.4=LN^2
Then we square root both sides of this equation:
LN=\sqrt{16.4}
LN=4.049691346...
LN=4.0 cm (1 dp).
Question 5: A builder places a 2.9 m ladder on horizontal ground, resting against a vertical wall. To be safe to use, the base of this ladder must be 1.3 m away from the wall. How far up the wall does the ladder reach?
Give your answer to 1 decimal place.
[2 marks]
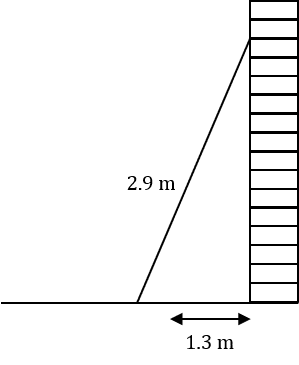
By substituting the known sides into Pythagoras’ Theorem c^2=a^2+b^2 (and letting the height of the wall be a) we get:
2.9^2=a^2+1.3^2
Calculating the two square roots and rearranging gives us:
a^2=8.41-1.69=6.72
Then by square rooting both sides of this equation, we get:
a=\sqrt{6.72}=2.592296279
a=2.6 cm (1 d.p.)
Pythagoras Worksheet and Example Questions
(NEW) Pythagoras Exam Style Questions - MME
Level 4-5GCSEPythagoras Drill Questions
Pythagoras 1 - Drill Questions
Level 4-5GCSE
