Classification of Particles
Classification of Particles Revision
Classification of Particles
There are a considerable number of different types of particles in the universe. This section will look at the properties of some of the most commonly found particles, hadrons and leptons.
Hadrons
Hadrons are particles that experience the strong nuclear force.
They are made up of smaller particles called quarks, hence are not a fundamental particle.
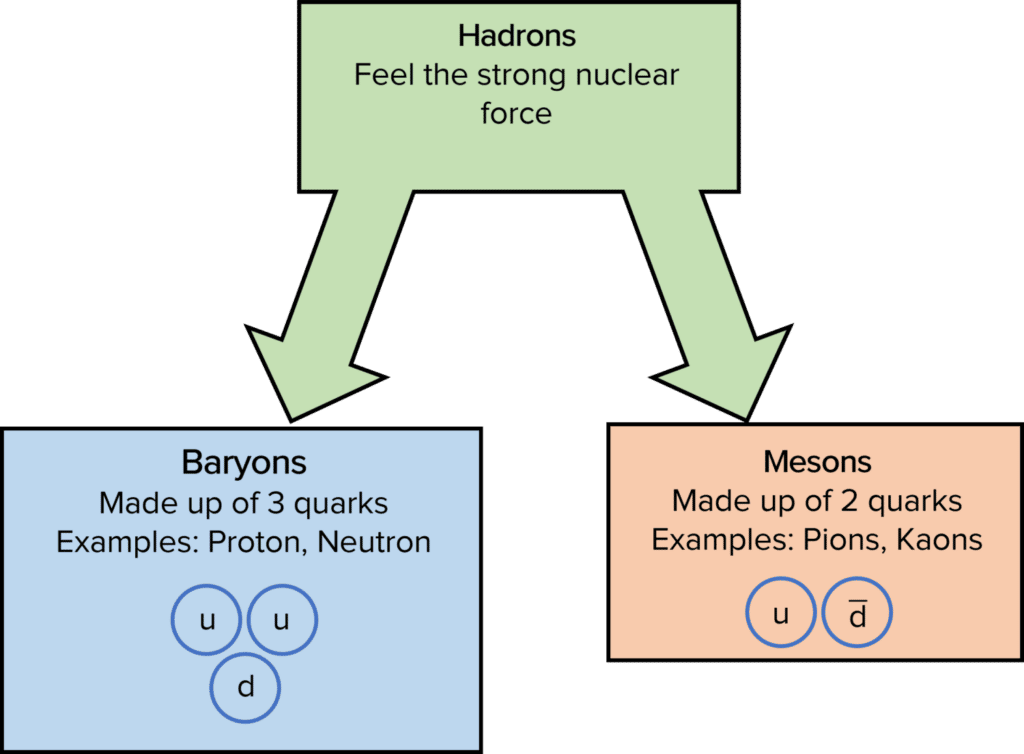

Hadrons have two sub-categories: baryons and mesons.
- Baryons are made up of 3 quarks. Examples of baryons include protons and neutrons.
- Mesons are made up of 2 quarks. Examples of mesons include pions and kaons.
Each hadron also has a corresponding anti-hadron e.g. anti-proton, anti-kaon. However, as antimatter is annihilated when in contact with matter, it is not possible to observe both together.
Only certain quark combinations are possible as all baryons and mesons must have an integer charge value.
Baryons
Baryons are hadrons with 3 quarks. The quarks are all the same type of quark; either 3 normal quarks (baryon) or 3 antiquarks (antibaryon).
Protons and neutrons are both baryons. There are other types of baryons, including sigmas \left(\Sigma\right) and lambdas \left(\Lambda\right), but these have very short half-lives and you don’t need to know them.
All particles have a baryon number \left(B\right). Baryons have a baryon number of B = 1, antibaryons have a baryon number of B = -1, with all other particles having a baryon number of B = 0.
The baryon number is a quantum number and is conserved for all particle interactions. This means that in a particle interaction, both sides of the equation must have the same baryon number. A quantum number can only take integer values.
All quarks have a baryon number of \dfrac{1}{3}, while all antiquarks have a baryon number of -\dfrac{1}{3}. The baryon number for each quark will be given on the datasheet.
Protons are the only stable baryon, all other baryons eventually decay to a proton. This is because protons are the lightest baryon and in general, radioactive decay causes heavier particles to decay to lighter particles. The half life of a proton has not been confirmed experimentally but it is theorised to be 1034 years.
Neutrons decay into protons through beta-minus decay, as shown in the diagram below. This decay is caused by the weak interaction. This occurs in a nucleus that is unstable due to the amount of neutrons or when a neutron is outside the nucleus. An electron and antineutrino are also formed in the decay, however as these are not baryons, they do not affect the total baryon number.
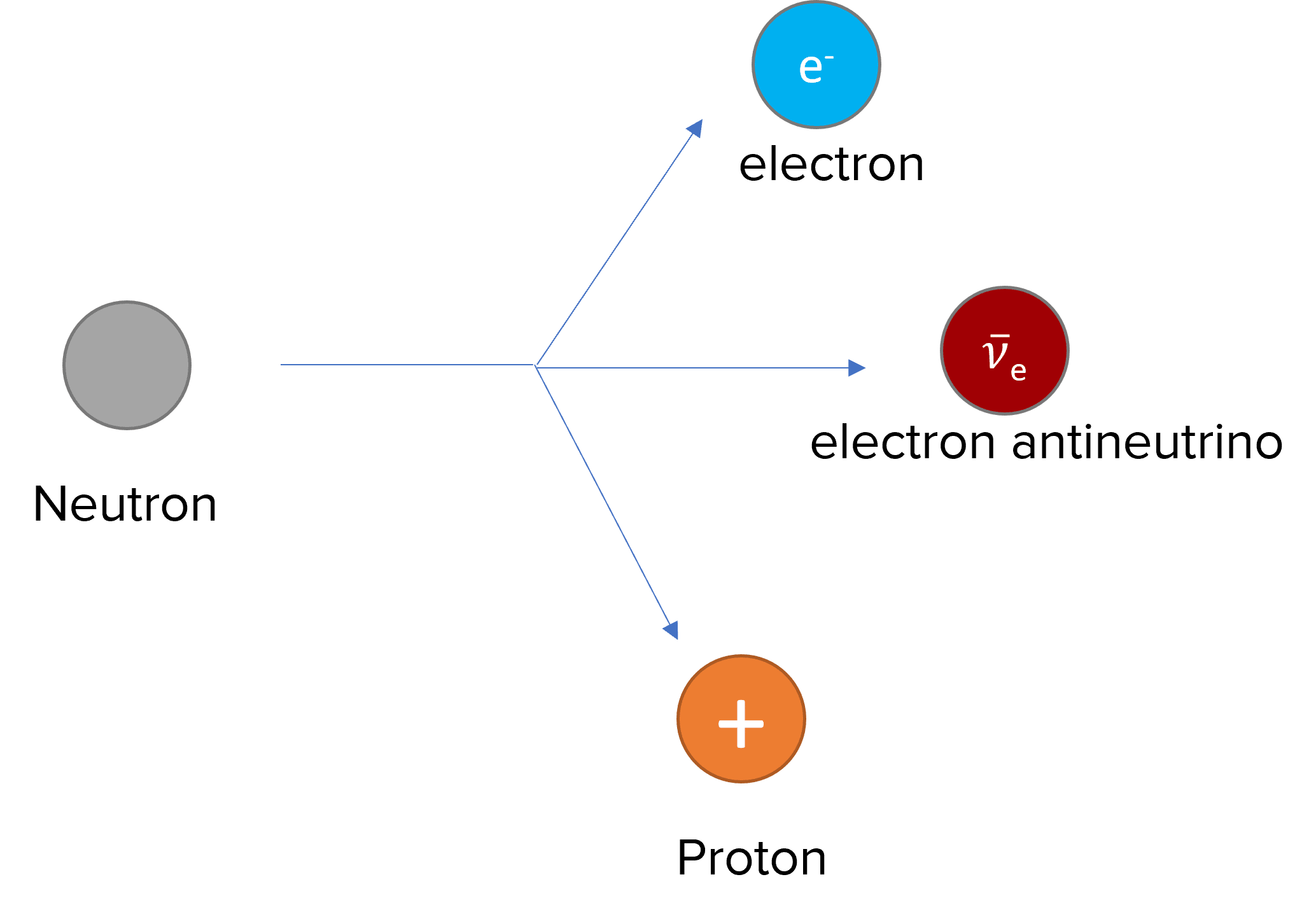
Therefore, baryon number is conserved in this interaction.
Mesons
Mesons are hadrons that are made up of a quark and an antiquark. They have a baryon number of B = 0 and can interact via the strong nuclear force.
Pions \left(\pi\right) are the lightest and most stable meson. There are different types of pions depending on the charge of the pion: \pi^+ \text{,} \: \pi^0 \text{,} \: \pi^- .
Pions can be produced in high energy particle collisions and were discovered in cosmic rays. They can be observed in cloud chambers.
They are a key component in the action of the strong nuclear force, which is one of the four fundamental interactions and holds nucleons together in the nucleus. Pions are the exchange particles for the strong nuclear force. This means that when the strong force acts between 2 nucleons, a pion is exchanged (passed between) them. In this situation, the pion is a virtual particle and therefore is not observed.
Kaons \left(K\right) are a heavier and less stable meson. They are produced by the strong interaction between pions and protons and eventually decay into pions. There are different types of kaons depending on the charge: K^+ \text{,} \: K^0 \text{,} \: K^-.
Kaons have long lifetimes, which is thought to be due to them containing a strange quark. They decay through the weak interaction and decay into pions.
Leptons
Leptons are a fundamental particle. They are not made up of any other particle.
They do not feel the strong nuclear force and interact with other particles through the electromagnetic, gravitational and weak interactions. Two examples of leptons that you need to know are the electron and muon.
Electrons are stable and have a relative charge of -1. Muons are heavier than electrons, making them more unstable but have the same charge as an electron.
Both leptons have their own neutrinos: electron neutrino and muon neutrino. Neutrinos have negligible mass and zero charge and only interact through the weak interaction. They are the most abundant leptons in the universe.
The lepton number is a quantum number that gives the number of leptons. There are two different types of lepton number, electron lepton number \left(L_e\right) and muon lepton number \left(L_{\mu}\right). Leptons and their corresponding neutrinos have a lepton number of +1, while antileptons and lepton antineutrinos have a lepton number of -1.
| Particle | Symbol | Relative Charge | \boldsymbol{L_e} | \boldsymbol{L_{\mu}} |
| electron | e^- | -1 | +1 | 0 |
| positron | e^+ | +1 | -1 | 0 |
| electron-neutrino | v_e | 0 | +1 | 0 |
| electron-antineutrino | \bar{v}_e | 0 | -1 | 0 |
| muon | \mu^- | -1 | 0 | +1 |
| antimuon | \mu^+ | +1 | 0 | -1 |
| muon-neutrino | v_{\mu} | 0 | 0 | +1 |
| muon-antineutrino | \bar{v}_{\mu} | 0 | 0 | -1 |
Muons and antimuons both decay into electrons and positrons respectively. This is because they are slightly heavier, therefore are more unstable. They decay through the weak interaction, through beta-minus and beta-plus decay:
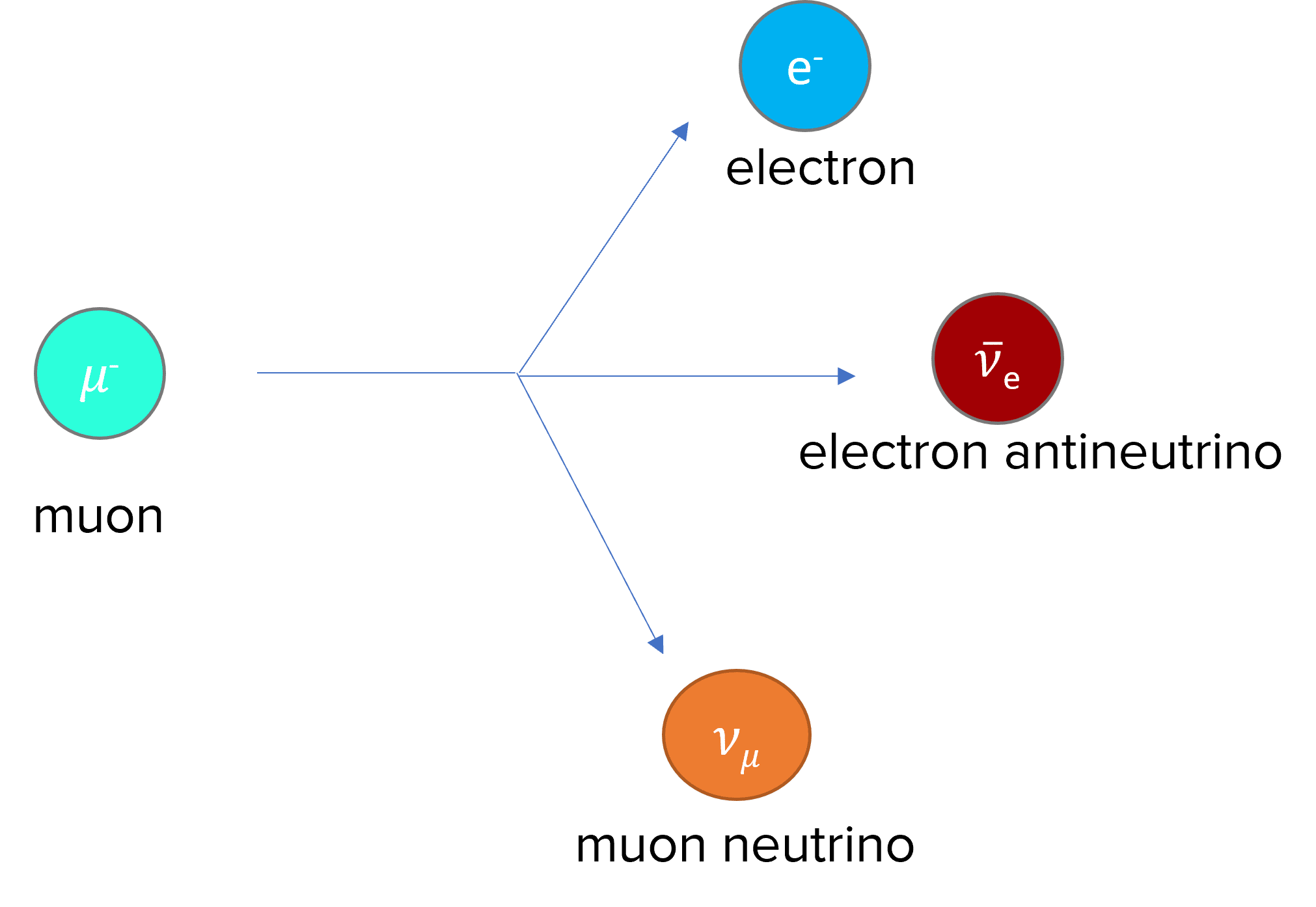
\mu^- \: \rightarrow \: e^- + \bar{v}_e + v_{\mu}
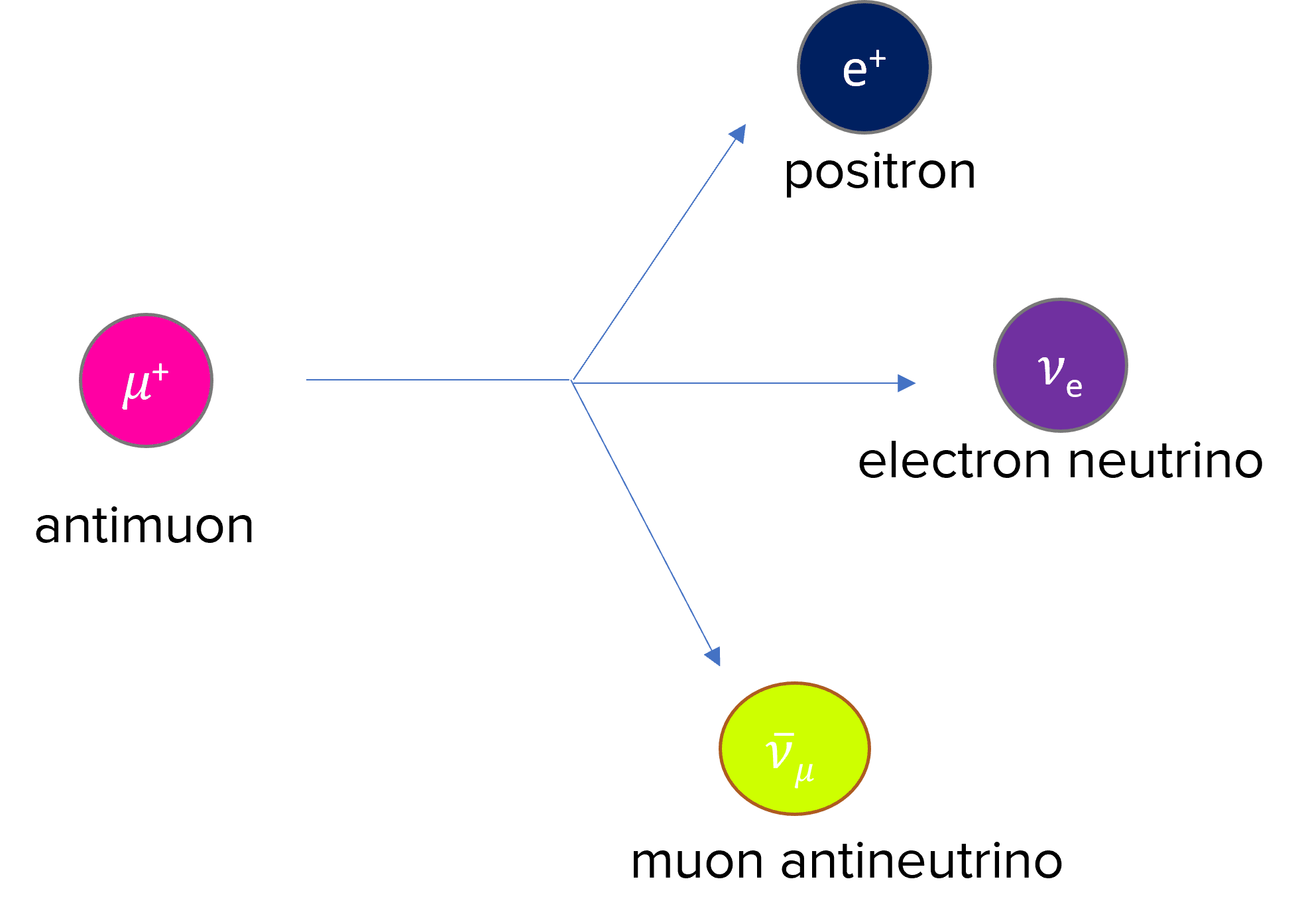
\mu^+ \: \rightarrow \: e^+ + v_e + \bar{v}_{\mu}
Note:
Remember that in all interactions, the quantum numbers are conserved. So for an interaction to take place, the baryon number and lepton number must be the same on both sides of the equation. This is also true for charge, as charge is conserved in interactions.
Example: Conservation of Quantum Numbers
By only checking the quantum numbers, is the following particle interaction possible?
n + \gamma \: \rightarrow e^- + e^+ + n
[2 marks]
-
We will check both the baryon numbers and lepton numbers for this interaction:
The \text{Baryon number} = 1 on both sides of the equation, and the \text{Lepton Number} = 0 on both sides of the equation. We do not need to check the Muon Lepton Number because there are no muons in this interaction. The quantum numbers are therefore conserved, and the particle interaction is possible.
Classification of Particles Example Questions
Question 1: Give 2 differences in the properties of hadrons and leptons.
[2 marks]
- Leptons are a fundamental particle, while hadrons are made of quarks.
- Hadrons can feel the strong force, while leptons cannot feel the strong force.
Question 2: What type of particle is the unknown particle X in the following interaction?
[1 mark]
By looking at the particles in the interaction, we only have hadrons. Therefore, we will look at the baryon number for the known particles.
\begin{aligned} p &+ \pi^+ \: \rightarrow K^0 + X \\ \textbf{Baryon Number:} \: 1 &+ 0 \: \rightarrow \: 0 \: + \: ? \end{aligned}Baryon number must be conserved in a particle interaction. Therefore X must have a Baryon Number of \boldsymbol{1}, and must be Baryon.
Question 3: Give the number of baryons, mesons and leptons in ^{23}_{11} Na.
[3 marks]
Sodium has 23 nucleons (protons and neutrons), which are all baryons.
Sodium does not contain any mesons.
Sodium has 11 electrons, which are leptons.
You May Also Like...

MME Learning Portal
Online exams, practice questions and revision videos for every GCSE level 9-1 topic! No fees, no trial period, just totally free access to the UK’s best GCSE maths revision platform.