Antiparticles and Photons

A LevelAS LevelAQA

Antiparticles and Photons Revision

Particles and Antiparticles

As far as we know, every particle in existence has a corresponding antiparticle. They share similar properties, aside from charge, and are created and annihilated together. In fact, a photon can create a particle and its corresponding antiparticle.

Photon

Photons are packets of electromagnetic energy. Photons can exist at a wide range of frequencies, represented by the electromagnetic spectrum, which is a continuous spectrum showing all possible frequencies of electromagnetic energy.

The frequency and wavelength of a photon are linked through the following equation:

$\textcolor{aa57ff}{f = \dfrac{c}{\lambda}}$

$\textcolor{aa57ff}{f}$ is the frequency in Hertz $\left(\text{Hz}\right)$ .
$\textcolor{aa57ff}{c}$ is the speed of light in a vacuum, $\textcolor{aa57ff}{3 \times 10^8 \: \text{ms}^{-1}}$ .
$\textcolor{aa57ff}{\lambda}$ is the wavelength in metres $\left(\text{m}\right)$ .

Electromagnetic energy is represented as photons, and the energy of a photon is dependent on the frequency or wavelength of the radiation through the following equation:

$\textcolor{aa57ff}{E = hf = \dfrac{hc}{\lambda}}$

$\textcolor{aa57ff}{E}$ is the energy of the photon, often in joules or electronvolts $\left(\text{J or eV}\right)$ .
$\textcolor{aa57ff}{h}$ is Planck’s constant, $\textcolor{aa57ff}{6.63 \times 10^{-34} \: \text{Js}}$
$\textcolor{aa57ff}{f}$ is the frequency in Hertz $\left(\text{Hz}\right)$ .

Remember that $1 \: \text{eV} = 1.6 \times 10^{-19} \: \text{J}$ .

Antiparticles

Every particle has a corresponding antiparticle.

An antiparticle has the same mass and rest energy as the particle but has the opposite charge.

The rest energy is the energy equivalent of a particle when that particle is at rest. It is commonly measured in $\text{MeV} \left(1 \: \text{MeV} = 1 \times 10^6 \: \text{eV} = 1.6 \times 10^{-13} \: \text{J}\right)$ .

The datasheet will provide the mass (in $\text{kg}$ ) and rest energy in (in $\text{MeV}$ ) for each particle.

Particle	Symbol	Relative Charge	Mass $\left(\textbf{kg}\right)$	Rest Energy $\boldsymbol{\left(\textbf{MeV}\right)}$
proton	$p$	$+1$	$1.673 \times 10^{-27}$	$938.3$
antiproton	$\bar{p}$	$-1$	$1.673 \times 10^{-27}$	$938.3$
neutron	$n$	$0$	$1.675 \times 10^{-27}$	$939.6$
antineutron	$\bar{n}$	$0$	$1.675 \times 10^{-27}$	$939.6$
electron	$e^-$	$-1$	$9.11 \times 10^{-31}$	$0.511$
positron	$e^+$	$+1$	$9.11 \times 10^{-31}$	$0.511$
neutrino	$v_e / v_{\mu}$	$0$	$0$	$0$
antineutrino	$\bar{v}_e / \bar{v}_{\mu}$	$0$	$0$	$0$

There are two types of neutrinos that you need to know, the electron neutrino and muon neutrino. They both have antiparticles. As neutrinos are so small, it is assumed that their mass and rest energy is zero.

Pair Production

New particles are always formed together in pairs; the particle and its antiparticle equivalent. For example, if a proton is formed then an antiproton must also be formed.

Matter and antimatter can be created from energy. Mass can be turned into energy and energy can turn into mass. This comes from Einstein’s Special Theory of Relativity.

The rest energy of a particle (measured in $\text{MeV}$ ) is the energy equivalent of a particle’s mass. When energy is converted into mass, equal amounts of matter and antimatter are produced.

One way this can occur is through collisions of high-speed particles. If you fire two protons at high speed at each other, there is a significant amount of energy at the collision point. If there is enough energy, then that energy may be converted to mass and form a particle and its corresponding antiparticle. For example, an electron and positron can be formed. This is an example of pair production.

Photons play a key role in pair production as energy is in the form of a photon before it is converted to matter and antimatter.

A single photon (usually a gamma ray) must have enough energy to produce both the particle and antiparticle. To conserve momentum, this usually happens near the nucleus of an atom. After the formation of the particles, they move in opposite directions, again for momentum conservation. Observations in particle physics experiments may show the particles having curved paths. This is due to there being a magnetic field present.

The most commonly produced pair is the electron and positron as they have a lower combined rest energy than other pairs. This is shown below in the diagram.

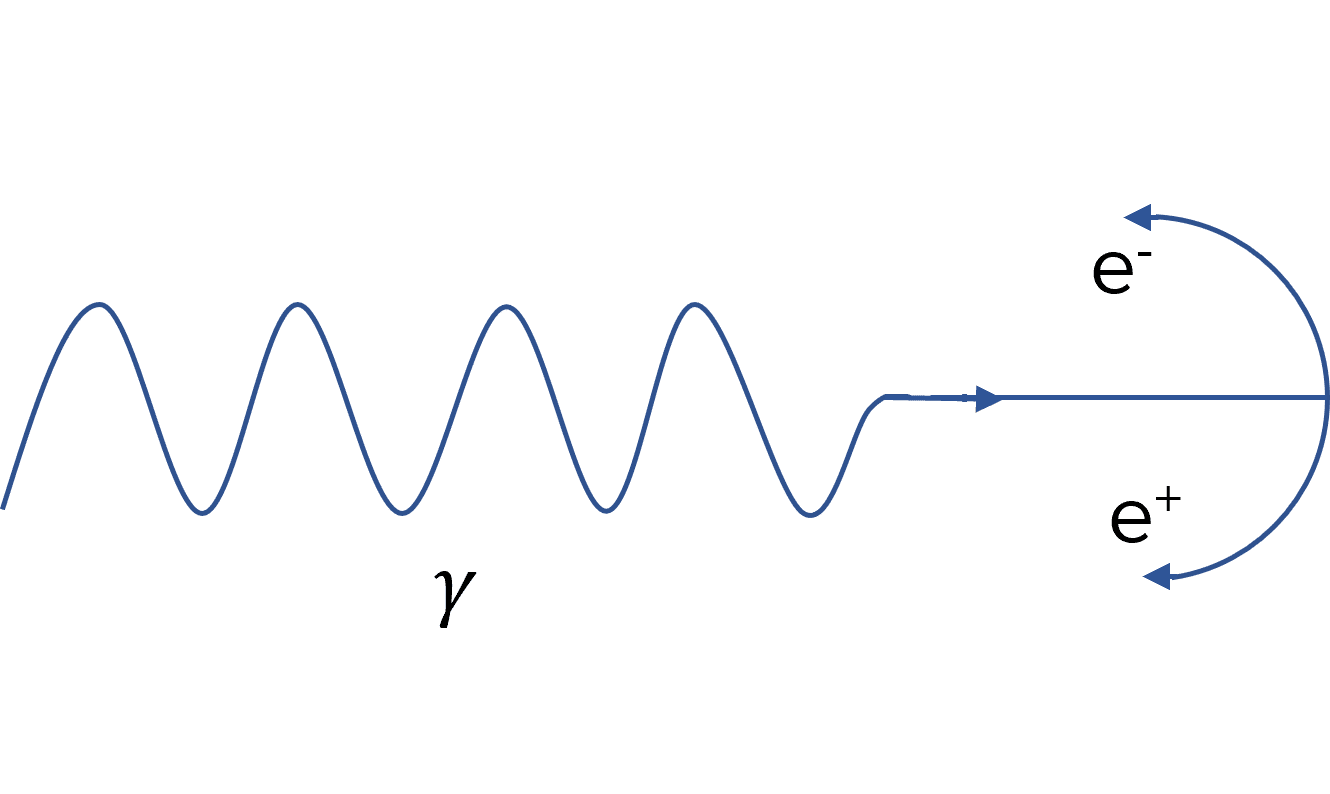
To calculate the minimum energy a photon needs to undergo pair production, you use the following equation:

$\textcolor{00bfa8}{E_{\text{min}} = hf = 2E_{\text{rest}}}$

$\textcolor{00bfa8}{E_{\text{min}}}$ is the minimum energy of the photon in joules or electronvolts $\left(\text{J or eV}\right)$ .
$\textcolor{00bfa8}{h}$ is Planck’s constant, $6.63 \times 10^{-34} \: \text{Js}$ .
$\textcolor{00bfa8}{E_{\text{rest}}}$ is the rest energy of the particles in joules or electronvolts $\left(\text{J or eV}\right)$ .
$\textcolor{00bfa8}{f}$ is the frequency in Hertz $\left(\text{Hz}\right)$ .

Example: Calculations involving Pair Production

Calculate the minimum frequency a photon needs to produce a proton through pair production.

[2 marks]

First, let’s get the correct equation needed to solve the question and rearrange:

$E_{\text{min}} = hf = 2E_{\text{rest}}$

$f = \dfrac{2E_{\text{rest}}}{h}$

We need to calculate the rest energy of a proton, you will be given this in the data sheet:

$\text{Proton Rest Energy} = 938.3 \: \text{MeV}$

In pair production, an antiparticle is produced, which will have the same rest energy:

$\text{Antiproton Rest Energy} = 938.3 \: \text{MeV}$

Convert the rest mass energy of one particle to joules:

$E_{\text{rest}} = 938.3 \: \text{MeV} = 938.3 \times 10^6 \times 1.6 \times 10^{-19} \: \text{J} = 1.50128 \times 10^{-10} \: \text{J}$

Substitute into the equation to find frequency:

$f = \dfrac{2 \left(1.50128 \times 10^{-10}\right)}{6.63 \times 10^{-34}} = 4.53 \times 10^{23} \: \text{Hz}$

Annihilation

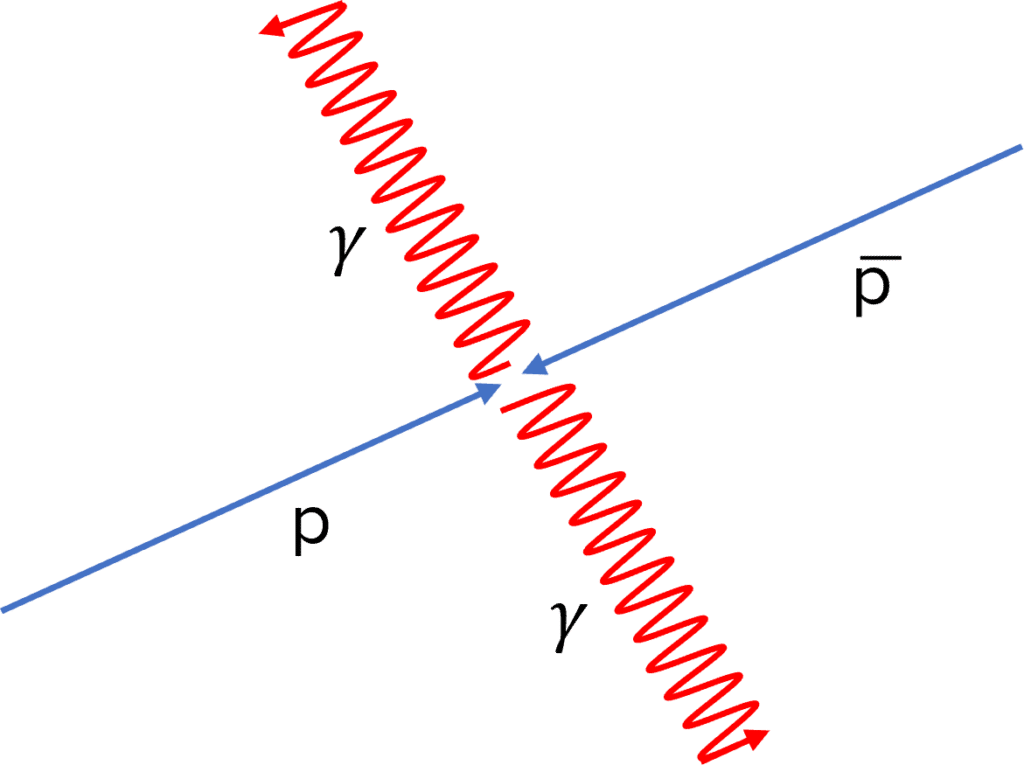
When a particle meets its antiparticle, both particles are turned back into energy through the process of annihilation.

Antiparticles only exist for a very short period of time as they quickly meet a particle.

Two photons are produced, whose minimum combined energy will equal the rest masses of the particles. The minimum energy of a energy released due to annihilation is given by the following equation:

$\textcolor{10a6f3}{E_{\text{min}} = hf_{\text{min}} = E_{\text{rest}}}$

$\textcolor{10a6f3}{E_{\text{min}}}$ is the minimum energy of the photon in joules or electronvolts $\left(\text{J or eV}\right)$ .
$\textcolor{10a6f3}{f_{\text{min}}}$ is the minimum frequency in Hertz $\left(\text{Hz}\right)$ .
$\textcolor{10a6f3}{E_{\text{rest}}}$ is the rest energy of the particles in joules or electronvolts $\left(\text{J or eV}\right)$ . Note that the rest energy of the particle and antiparticle is the same.

The photons will travel in opposite directions in order to conserve momentum.

Example: Calculations involving Annihilation

Calculate the wavelength of the photons released when a proton and antiproton annihilate each other.

[2 marks]

First, let’s get the correct equation needed to solve the question:

$E_{\text{min}} = hf = E_{\text{rest}}$

We need to find the wavelength, therefore we use the wave equation to find the correct equation:

$f = \dfrac{c}{\lambda}$

$\dfrac{hc}{\lambda} = E_{\text{rest}}$

$\dfrac{hc}{E_{\text{rest}}} = \lambda$

We need to use the rest energy of a proton, you will be given this in the data sheet. Remember that both a particle and its antiparticle will have the same rest mass:

$\text{Proton Rest Energy} = 938.3 \: \text{MeV}$

The rest energy needs to be converted to joules:

$E_{\text{rest}} = 938.3 \: \text{MeV} = 938.3 \times 10^6 \times 1.6 \times 10^{-19} \: \text{J} = 1.5 \times 10^{-10} \: \text{J}$

Substitute into the equation to find the wavelength:

$\lambda = \dfrac{6.63 \times 10^{-34} \times 3.0 \times 10^8}{1.5 \times 10^{-10}} = 1.3 \times 10^{-15} \: \text{m}$