Trig Graphs
Trig Graphs Revision
Trig Graphs
Back in Trig Basics, we showed you the trig graphs in a pretty simple form. We’ll be looking at a few different transformations of those graphs in this section.
A Quick Reminder
Here’s the \textcolor{blue}{\sin x} graph…
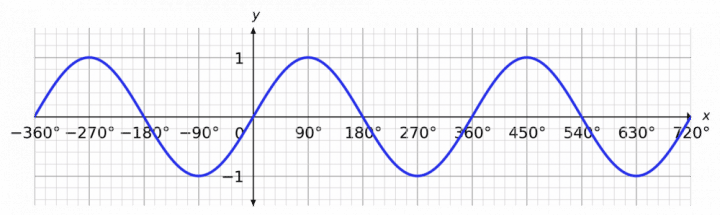
and the \textcolor{limegreen}{\cos x} graph…
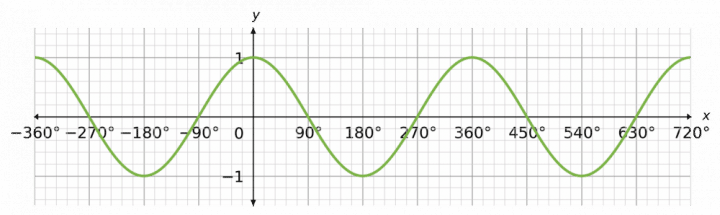
… and also the \textcolor{red}{\tan x} graph.
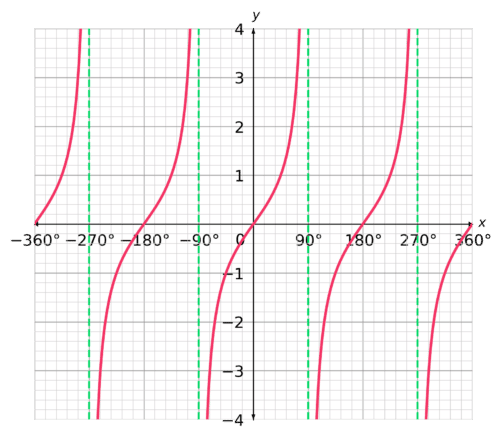
So, the \textcolor{blue}{\sin x} and \textcolor{limegreen}{\cos x} graphs have a periodicity of 360°, while the \textcolor{red}{\tan x} has a periodicity of 180°.
To help you remember, we have these three rules:
- \textcolor{blue}{\sin x} = \sin (x + 360°) = \sin (x - 360°)
- \textcolor{limegreen}{\cos x} = \cos (x + 360°) = \cos (x - 360°)
- \textcolor{red}{\tan x} = \tan (x + 180°) = \tan (x - 180°)
Now, it’s time to take a look at some transformations.
Vertical Translation
We’ll start with something nice and simple – a vertical translation.
So, below we’ve got a graph of \textcolor{blue}{y = \sin x}. Nothing out of the ordinary there.
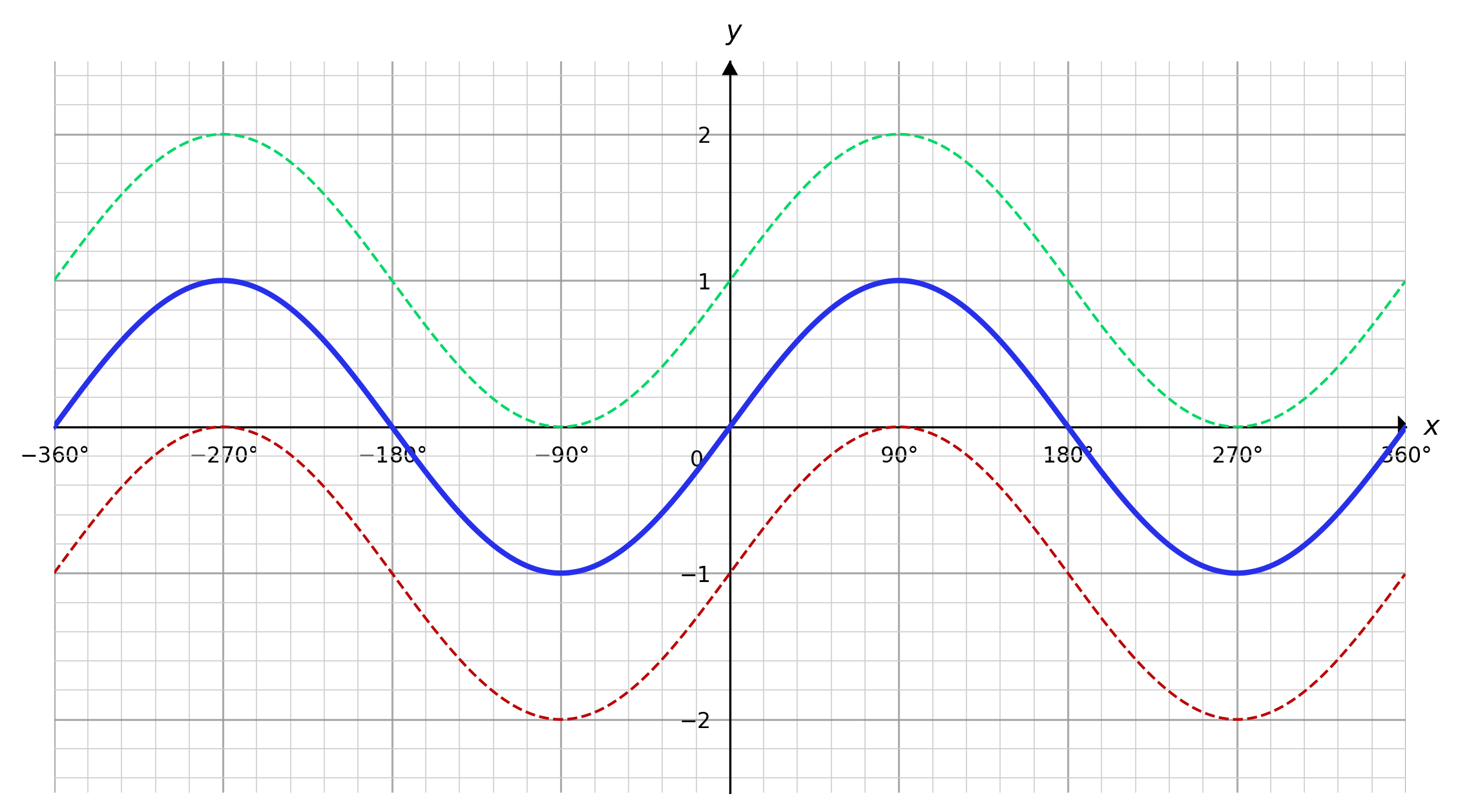
We also have two vertical translations, \textcolor{limegreen}{y = (\sin x) + 1} and \textcolor{red}{y = (\sin x) - 1}.
Horizontal Translation
We also have horizontal translations, where the transformation acts directly on x.
Again, we’ll start with \textcolor{blue}{y = \sin x}.
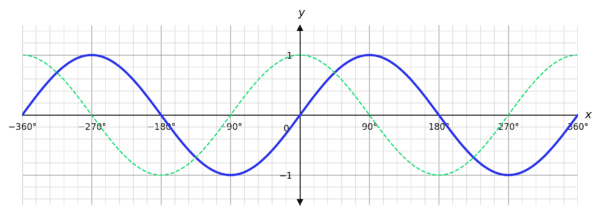
Now we’ve got a horizontal translation, \textcolor{limegreen}{y = \sin (x + 90°)}.
In short, a transformation y = \sin (x + c) is a translation to the left of c. So, if you have \sin (x - 45°), for example, it is a translation 45° to the right.
In other words, a transformation of y = \sin (x + c) is a translation of -c along the x-axis
Vertical Stretching
Now, we’ll introduce vertical stretching to our repertoire.
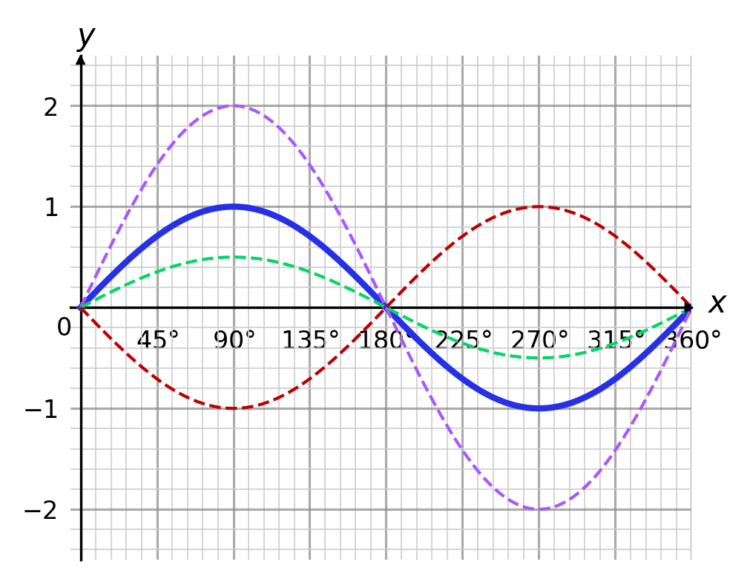
We have three transformations of \textcolor{blue}{y = \sin x} here:
- \textcolor{purple}{y = 2\sin x}
- \textcolor{limegreen}{y = \dfrac{1}{2}\sin x}
- \textcolor{red}{y = -\sin x}
Horizontal Stretching
We’ll take a look at horizontal stretching now, too.
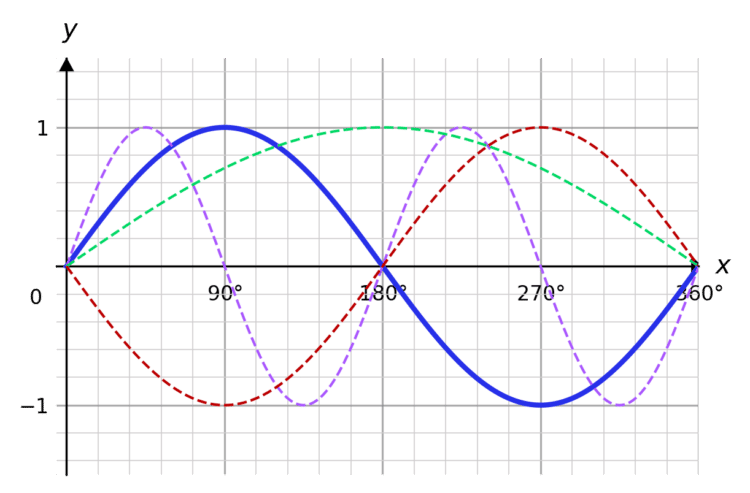
We have three transformations of \textcolor{blue}{y = \sin x}:
- \textcolor{purple}{y = \sin (2x)}
- \textcolor{limegreen}{y = \sin \left( \dfrac{1}{2}x \right)}
- \textcolor{red}{y = \sin (-x)}
A Handy Table
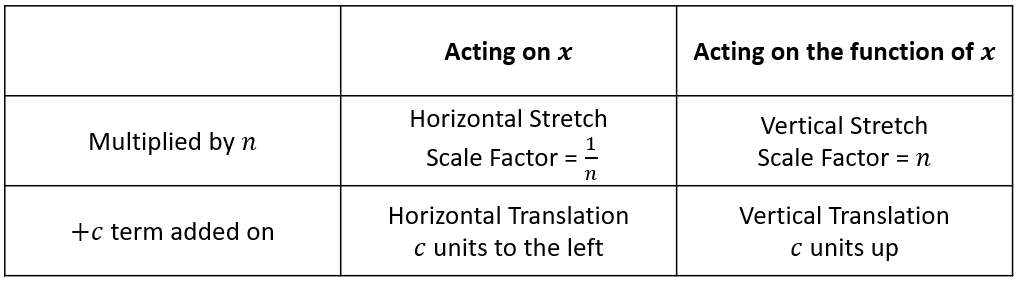
Trig Graphs Example Questions
Question 1: Sketch the graphs for \sin x, \cos x and \tan x, indicating all points where the graph meets either axis. For \tan x, label the asymptotes, also. Take 0° \leq x \leq 360°.
[3 marks]
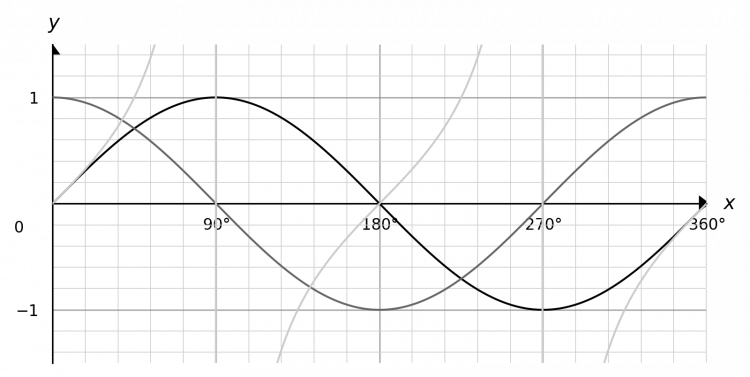
\sin x meets the y axis at y = 0, and the x axis at x = 0°, 180°, 360°.
\cos x meets the y axis at y = 1, and the x axis at x = 90°, 270°.
\tan x meets the y axis at y = 0, and the x axis at x = 0°, 180°, 360°. Its asymptotes lie at x = 90, 270°.
Question 2: State the range of values that y can take, for the graphs:
- y = 2 - 3\sin x
- y = \cos \left( 2x - \dfrac{\pi}{2}\right)
- y = \dfrac{1}{2}\tan x
[5 marks]
y = 2 - 3\sin x is a vertical stretch with a scale factor of -3, and vertical translation of +2. Therefore, its range goes from -1 \leq y \leq 1 \to -3 \leq y \leq 3 \to -1 \leq y \leq 5.
y = \cos \left( 2x - \dfrac{\pi}{2}\right) is a horizontal stretch with a scale factor of \dfrac{1}{2}, and a horizontal translation of \dfrac{+\pi}{2}. There is no vertical transformation, so the range stays at -1 \leq y \leq 1.
y = \tan x has an infinite range, so y = \dfrac{1}{2}\tan x also has an infinite range, meaning -\infty \leq y \leq \infty.
Question 3: Describe the three transformations, involved in the single transformation from y = \sin x to y = 3\sin \left( \dfrac{x}{2} + \dfrac{\pi}{3}\right) .
[6 marks]
We need to take the transformations in the order that they affect x. So,
- \sin x \to \sin \dfrac{x}{2} is a horizontal stretch with scale factor 2
- \sin \dfrac{x}{2} \to \sin \left( \dfrac{x}{2} + \dfrac{\pi}{3}\right) is a horizontal translation, \dfrac{\pi}{3} units to the left
- \sin \left( \dfrac{x}{2} + \dfrac{\pi}{3}\right) \to 3\sin \left( \dfrac{x}{2} + \dfrac{\pi}{3}\right) is a vertical stretch with scale factor 3
Note:
We could alternatively have Step 3 at the beginning, but Steps 1 and 2 must be in the order they are in.
Trig Graphs Worksheet and Example Questions
Curve Sketching
A LevelYou May Also Like...

MME Learning Portal
Online exams, practice questions and revision videos for every GCSE level 9-1 topic! No fees, no trial period, just totally free access to the UK’s best GCSE maths revision platform.






