Sampling Techniques
Sampling Techniques Revision
Sampling Techniques
Sampling techniques are the methods by which we choose a representative sample from a population. There are six sampling techniques that you need to know about.
Make sure you are happy with the following topics before continuing.
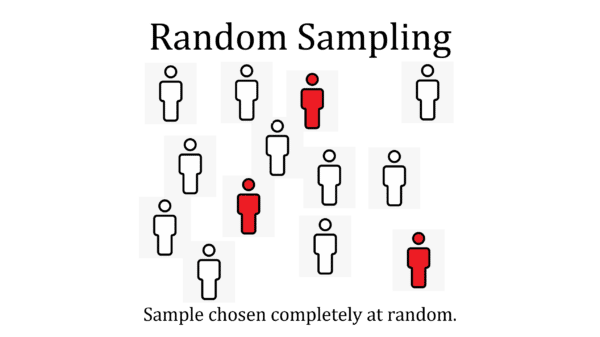
Skill 1: Random Sampling
In a random sample, every unit in the population is equally likely to be selected, and each selection is independent of every other selection.
One way to do this is to assign every unit in the population a unique random number, then select numbers at random, then select the units that correspond to those numbers.
Random sampling has the advantage of being completely unbiased (because every member of the population has an equal chance of being selected), but the disadvantage of the chosen sample might not represent the population very well because of random fluctuations.
Skill 2: Systematic Sampling
A systematic sample selects every nth member of a population.
To create a systematic sample, give every member of the population unique, sequential numbers, then select a start number a, then a+n, then a+2n, etc. Choose a randomly but less than n and choose n such that you get the sample size you desire.
This method has the advantage that it does not involve random elements, so could be performed very quickly by a machine. It has the disadvantage that the method could coincide with a pattern.
For example, this method fails if we sample every 5 items from a production line, but the machine has an error every fifth item. We either find that every item is faulty or none are, when the real fault rate is 20\%.

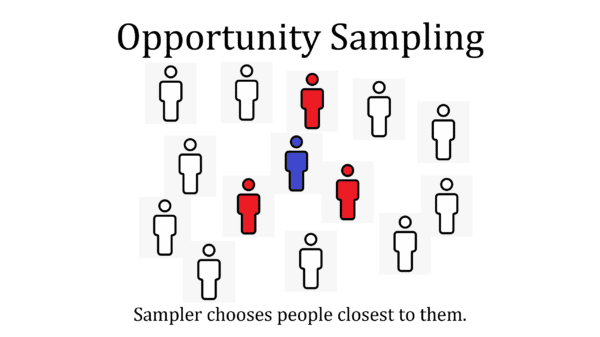
Skill 3: Opportunity Sampling
Opportunity or convenience sampling is a sample based on what is convenient for the sampler. For example, it could be a survey handed out to the friends and family of the sampler because this is easier than contacting people they do not know.
Opportunity sampling is a generally poor method of sampling. Although it may be quick and easy, it is clearly biased, and no attempt to obtain a representative sample has been made.
Skill 4: Stratified Sampling
A stratified sample looks at a way in which the population has been divided into categories and samples accordingly. For example, to sample 15 from a population of 300 that has been split into categories of 200 and 100 we would sample 10 from the first category and 5 from the second category. Within a category we randomly sample the population of that category.
To calculate the size of a category in the sample, we use this formula:
\text{size of category in sample}=\dfrac{\text{size of category in population}}{\text{size of population}}\times\text{total sample size}
Skill 5: Quota Sampling
In quota sampling, we sample within categories that the population has already been divided into like in stratified sampling. However, rather than make the amount sampled from each category representative of the size of the category in the population, we set a quota for each category then perform opportunity sampling in each category until that category’s quota is met.
An advantage of this is that it can approximate stratified sampling when a full population list is not available. Another advantage is that the setting of quotas can be done by any metric, meaning that categories can be weighted differently than according to their size if desired. A disadvantage is that this choosing of quotas can easily cause the sample to be biased.
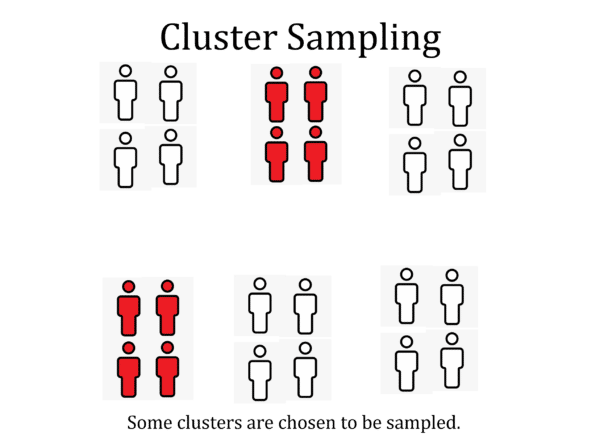
Skill 6: Cluster Sampling
(This section is not on Edexcel.)
To perform a cluster sample, first divide the population into clusters, such that every member of the population is in exactly one cluster. You should not divide the population into clusters based on any particular characteristic – rather, the population should be divided in a random or representative way. Then, we randomly select clusters to sample. For a one stage cluster we then use every member of the selected clusters in our sample. For a two stage cluster we randomly sample within the selected clusters to get our final sample.
An advantage of cluster sampling is that it could be more practical or cheaper, since large amounts of the population are discounted when clusters are selected. A disadvantage is that this discounting of populations means that not the whole population is included in the sampling frame, which could cause some sampling bias.
Note: The difference between categories and clusters is that different categories would be likely to give different results to each other, while clusters should give similar results.
Sampling Techniques Example Questions
Question 1: Mr. Hobbes performs a stratified sample of students in his school. There are 1500 students, of which he wants to sample 50, stratified by year group. The table below gives the number of students in each year group.
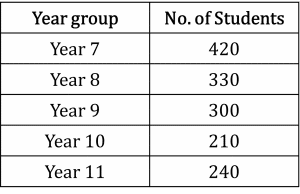
a) How many students from each year group should be selected for the sample?
b) If Mr. Hobbes did not know the size of each year group, suggest which sampling method he could use to still break down sampling by year group.
[5 marks]
a) \text{Year 7}=\dfrac{420\times50}{1500}=14
\text{Year 8}=\dfrac{330\times50}{1500}=11
\text{Year 9}=\dfrac{300\times50}{1500}=10
\text{Year 10}=\dfrac{210\times50}{1500}=7
\text{Year 11}=\dfrac{240\times50}{1500}=8
b) Quota sampling
Question 2: Kate asks her friends to fill in a survey for her insurance company. What kind of sampling is this? Why is it unlikely to be representative?
[2 marks]
This is opportunity sampling.
It is unlikely to be representative because Kate’s friends could all share traits that are not shared by the wider population (e.g. they could all be similar ages).
Question 3: A machine picks every fifth bag off a luggage conveyer belt in an airport in order to examine its weight to determine if the scales at check-in desks are working.
a) What kind of sampling is this?
b) If the check-in desk scales are wrong on every tenth read, what are the two possible conclusions the machine will reach?
[3 marks]
a) This is systematic sampling because we are sampling each one at a fixed interval.
b) If our machine is offset from these one in ten, we would find that the scales at check-in are never wrong.
If our machine samples every fifth in a way that lines up with this one in ten, we would find that the scales at check-in are wrong half the time.
Question 4: Allison wants to sample the people of Scarborough for a news article about living on the coast. She has no demographic information for the town. Suggest why a random sample would be most appropriate.
[3 marks]
No demographic information means not enough information to divide the population into categories, so we can discount stratified and quota sampling.
There is no obvious numbering that would not just be random, so systematic sampling would not work.
Opportunity sampling and cluster sampling are both more biased than random sampling in a population that nothing is known about.
Hence, random sampling is the most appropriate.
Question 5: A teacher wants to sample their English language students, who are split across three classes. Given that students are placed into a class at random at the start of an academic year, explain how cluster sampling might allow them to only select students from one class.
[2 marks]
Each class is its own cluster, because they are each a random selection of the entire student population. So we can select only one class (one cluster) at random to sample from.







