Probability and Venn Diagrams
Probability and Venn Diagrams Revision
Probability and Venn Diagrams
Probability is a measure of how likely something is to happen.
It always falls between \mathbf{0} and \mathbf{1}, with 0 being impossible and 1 being certain.
Notation: The probability of an event A is \mathbb{P}(A).
Calculating Probabilities
To calculate the probability of an event, the formula is:
\dfrac{\color{red}\text{number of desired outcomes}}{\color{blue}\text{total number of possible outcomes}}
Example: What is the probability of obtaining an even number when rolling a 6-sided die?
Our possible outcomes are \color{blue}1,2,3,4,5,6, of which \color{red}2,4,6 are even. This gives \color{red}3 desired outcomes, out of \color{blue}6 possible outcomes, so:
\mathbb{P}(\text{roll an even number})=\dfrac{\color{red}3}{\color{blue}6}=\dfrac{\color{red}1}{\color{blue}2}
AND & OR
A\cap B means \mathbb(A) AND \mathbb(B) – that both event A and event B happen.
A\cup B means \mathbb(A) OR \mathbb(B) – that event A happens or event B happens (or both).
The probabilities of A\cap B and A\cup B are related by the formula:
\mathbb{P}(A\cup B)=\mathbb{P}(A)+\mathbb{P}(B)-\mathbb{P}(A\cap B)
These probabilities can be calculated with a Venn Diagram.
Example: considering dice again, if A is “rolls a multiple of 3” and B is “rolls 3 or 4”, then we have:
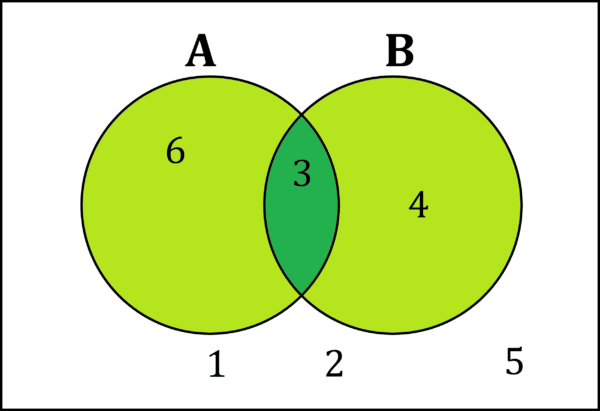
By looking at where the circles overlap, we notice there is one value, so A\cap B contains one value.
By looking at the circles in their entirety, we notice that there are 3 values contained within circle A or circle B, so A\cup B contains three values.
Since there are six values overall, we can conclude:
\mathbb{P}(A\cap B)=\dfrac{1}{6}
\mathbb{P}(A\cup B)=\dfrac{3}{6}=\dfrac{1}{2}
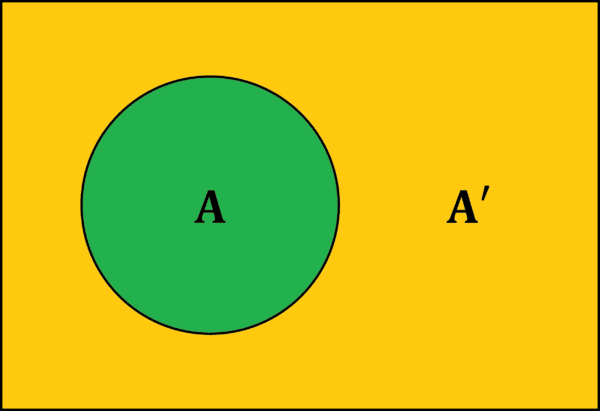
Complement of an Event
The complement of an event is the event that it doesn’t happen, for example if A is rolls a 3 or 4 then the complement of A, written A', is does not roll a 3 or 4, i.e. rolls a 1,2,5 or 6.
Since any event definitely either does or does not happen, the probability of an event and its complement must add to \mathbf{1}.
\mathbb{P}(A)+\mathbb{P}(A')=1
On a Venn Diagram, the complement of A is everything not contained within the circle representing A.
Two-Way Tables
Two way tables model two events, A and B, by displaying every combination of whether or not each one happens. They can either display frequency (which should be familiar from GCSE) or probability. If it displays probability, then the numbers in it excluding row totals and column totals must add to \mathbf{1}, and the final total in the bottom right must be 1. An example is given below.

Note: the totals are probabilities for one event, e.g. the total in the A column is the probability of event A. Using this, we can create the most general form of a two-way table:

Probability and Venn Diagrams Example Questions
Question 1: Inside a bag are 3 red marbles and 8 green marbles. Cate picks one marble at random. What is the probability that she has picked a green marble?
[1 mark]
There are 11 marbles, representing 11 possible outcomes, and 8 marbles that give the desired outcome, so the probability is \dfrac{8}{11}.
Question 2: If A has probability 0.4 and B has probability 0.3, what is \mathbb{P}(A\cup B)+\mathbb{P}(A\cap B)?
[2 marks]
\mathbb{P}(A\cup B)=\mathbb{P}(A)+\mathbb{P}(B)-\mathbb{P}(A\cap B)
\mathbb{P}(A)=0.4
\mathbb{P}(B)=0.3
\begin{aligned}\mathbb{P}(A\cup B)&=0.4+0.3-\mathbb{P}(A\cap B)\\[1.2em]&=0.7-\mathbb{P}(A\cap B)\end{aligned}
\mathbb{P}(A\cup B)+\mathbb{P}(A\cap B)=0.7
Question 3: Consider flipping a coin three times. Event A is that the second flip is tails. Event B is that there are at least two heads.
a) Represent the events A and B on a Venn Diagram.
b) Find \mathbb{P}(A)
c) Find \mathbb{P}(B)
d) Find \mathbb{P}(A\cap B)
e) Find \mathbb{P}(A\cup B)
f) How many possibilities do not fall within the Venn Diagram at all?
[6 marks]
a)
b) 8 total events, 4 of them in circle A, so probability is \dfrac{4}{8}=\dfrac{1}{2}
c) 8 total events, 4 of them in circle B, so probability is \dfrac{4}{8}=\dfrac{1}{2}
d) This corresponds to where the circles overlap, which contains one event, so probability is \dfrac{1}{8}
e) This corresponds to both circles, which contain 7 events, so probability is \dfrac{7}{8}
f) 1 possibility does not lie within the Venn Diagram
Question 4: An event has probability 0.932. What is the probability of its complement?
[1 mark]
Question 5: Complete the two-way table and use it to determine \mathbb{P}(A\cap B')

[4 marks]

You May Also Like...

MME Learning Portal
Online exams, practice questions and revision videos for every GCSE level 9-1 topic! No fees, no trial period, just totally free access to the UK’s best GCSE maths revision platform.






